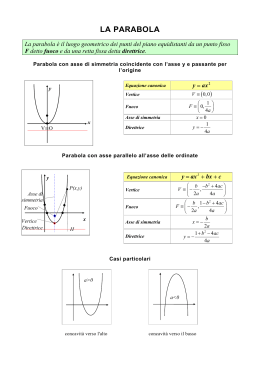
LA PARABOLA
Definizione
• Dicesi parabola il luogo dei punti P di un piano Ω
equidistanti da un punto assegnato F ( detto
FUOCO) e da una retta data r detta DIRETTRICE
con F  r
S ed H sono le
proiezioni sulla retta r.
V è il punto medio del
segmento FH e si
chiama VERTICE.
EQUAZIONE DELLA PARABOLA
• Assumiamo come
asse delle ordinate la
perpendicolare per F
alla direttrice e come
O il punto medio del
segmento FH cioè il
vertice della parabola.
Y= - p/2
Dalla definizione sappiamo che FP=PS, calcolando nel solito modo la distanza tra i
Due segmenti troviamo
2
x
y=
2p
Posto a = 1/2p si trova
y=a
x
2
il vertice si trova nell' origine degli assi O (0,0);
1
il fuoco è il punto F (0, );
4a
l' asse di simmetria è l' asse y, cioè la retta x  0;
1
la direttrice è la retta y  4a
LA PARABOLA SI TROVA SOPRA L’ASSE X SE A è
POSITIVO, AL DI SOTTO DELL’ASSE X SE A è NEGATIVO
y = ax2 + bx + c
LA PARABOLA è SOTTO L’ASSE X
• GRAFICO
Y=
AX
2
 BX  C
• RAPPRESENTA L’EQUAZIONE
•
•
GENERALE DI UNA PARABOLA
b
b
 4 ac
,
V(- 2
)
a
2a
F(  b 1
b  4ac )
2
2a
,
4a

2
• Asse di simmetria x =
• Direttrice y =
4a
 b
2a
1 b 2  4ac
(

)
4a
4a