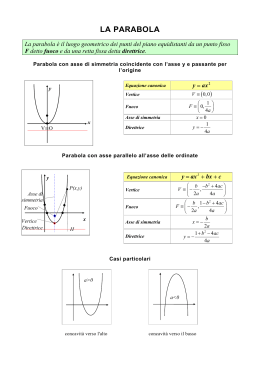
La parabola è il luogo geometrico dei punti del piano equidistanti del
punto fisso F(detto fuoco) e da una retta data d(detta direttrice)
Equazione della parabola con vertice nell' origine e asse
di simmetria coincidente all' asse y
y=ax^2
Caratteristiche della parabola di equazione y=ax^2
a >0
a <0
vertice
asse di simmetria
fuoco
direttrice
--->la concavità è verso l' alto
--->la concavità è verso il basso
---> O(0;0)
--->x=0
--->F(0;1/4a)
--->y=-1/4a
Equazione della parabola con centro nell' origine e asse di
simmetria coincidente all' asse x
x=ay^2
Caratteristiche della parabola di equazione x=ay^2
a >0
a <0
vertice
asse di simmetria
fuoco
direttrice
--->la concavità è verso destra
--->la concavità è verso sinistra
---> O(0;0)
--->y=0
--->F(1/4a;0)
--->x=-1/4a
Equazione della parabola con asse di simmetria parallelo all' asse y
Usando le equazioni della traslazione degli assi,
otteniamo:
x-xo=a(x-xo)^2
Sviluppando i calcoli e sostituendo:
-2axo=b e axo^2+yo=c
Otteniamo l' equazione generica della parabola
y=ax^2+bx+c
Caratteristiche della parabola di equazione y=ax^2+bx+c
a >0
a <0
vertice
asse di simmetria
fuoco
direttrice
--->la concavità è verso l' alto
--->la concavità è verso il basso
---> V(-b/2a;-Δ/4a)
--->x=-b/2a
--->F(-b/2a;-(1-Δ/4a))
--->y=-((1+Δ)/4a)
Equazione della parabola con asse di simmetria parallelo all' asse x
Se operiamo analogamente alla parabola cn asse di
simmetria parallelo all' asse y, otteniamo:
x=ay^2+by+c
Caratteristiche della parabola di equazione x=ay^2+by+c
a >0
a <0
vertice
asse di simmetria
fuoco
direttrice
--->la concavità è verso destra
--->la concavità è verso sinistra
---> V(-Δ/4a;-b/2a)
--->y=-b/2a
--->F(-(1-Δ/4a);-b/2a)
--->x=-((1+Δ)/4a)
L’ ARCO DI ST. LOUIS
Applicazione reale di una parabola