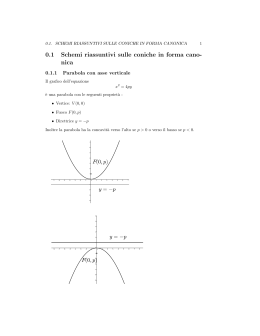
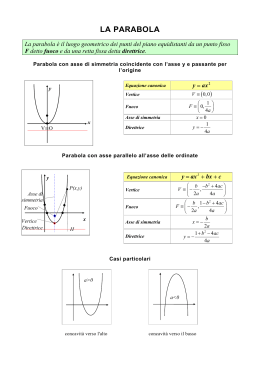
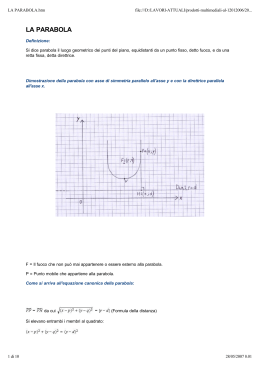
Le coniche
LA PARABOLA
Le coniche
Circonferenza
Parabola
Ellisse
Iperbole
Le coniche
• Le coniche sono curve studiate sin dall'antichità e molti matematici hanno
dato il loro contributo al loro studio.
• Menecmo (375-325 a.C.), matematico greco maestro di Alessandro Magno,
dimostra come ellissi, parabole e iperboli si possono ottenere tagliando un
cono con un piano non parallelo alla base.
• Apollonio (262-190 a.C.), conosciuto come il Grande Geometra, consolidò
ed approfondì i risultati sulle coniche nell'opera Le Coniche. Fu anche il
primo ad attribuire i nomi di ellisse, parabola, ed iperbole.
La parabola
Assegnato un punto F e una retta d si chiama parabola il luogo geometrico dei
punti equidistanti da F e d
Asse di simmetria
Parabola con asse parallelo all’asse y
y = ax 2 + bx + c a ¹ 0
Asse di simmetria:
Vertice:
Fuoco
Fuoco:
Vertice
direttrice
x=-
æ b
Dö
V ç - ;- ÷
è 2a 4a ø
æ b 1- D ö
F ç- ;
÷
è 2a 4a ø
Direttrice: y = D = b 2 - 4ac
1+ D
4a
b
2a
Parabola con asse parallelo all’asse y
y = ax 2 + bx + c a > 0
Concavità rivolta verso l’alto
y = ax 2 + bx + c a < 0
Concavità rivolta verso il basso
Per a>0, all’aumentare di a diminuisce l’apertura della parabola
Rappresentare sul piano cartesiano la parabola di equazione:
y = x 2 - 2x - 3
Asse di simmetria:
x=-
b
® x =1
2a
D = b 2 - 4ac = 16
Vertice:
æ b
Dö
V ç - ;- ÷ ® V (1;-4)
è 2a 4a ø
Fuoco:
æ b 1- D ö
æ 15 ö
F ç- ;
®
F
÷
ç1;- ÷
è 2a 4a ø
è
4ø
Direttrice: y = -
1+ D
17
®y=4a
4
Intersezione con gli assi cartesiani:
A ( -1;0)
B(3;0)
Parabola con asse parallelo all’asse x
x = ay 2 + by + c a ¹ 0
Asse di simmetria:
Vertice:
Fuoco:
y=-
æ D
bö
V ç - ;- ÷
è 4a 2a ø
æ 1- D b ö
Fç
;- ÷
è 4a
2a ø
Direttrice: x = -
1+ D
4a
D = b 2 - 4ac
a>0 concavità rivolta verso destra; a<0 concavità rivolta verso sinistra
b
2a