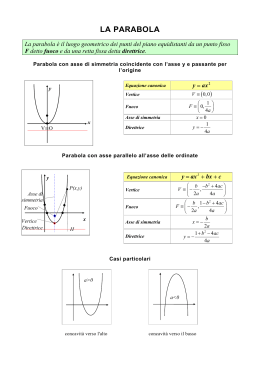
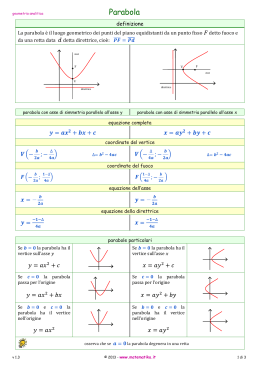
Costruzione della Parabola
con Geogebra
A.S. 2011-12
Parabola
Definizione:
• La parabola è il luogo geometrico dei
punti del piano equidistanti da un
punto fisso F (detto fuoco) e da una
retta d (detta direttrice).
Metodo 1
Fissata una distanza k, tracciamo
la circonferenza di centro F e
raggio k e la retta parallela alla
direttrice a distanza k da essa.
I due punti di intersezione tra la
circonferenza e la retta hanno
distanza k sia dal punto F che
dalla retta d, dunque
appartengono alla parabola:
i due punti sono simmetrici
rispetto all’asse della parabola.
Quindi per ogni valore k, possiamo
tracciare due punti della parabola
purché k sia maggiore della metà
della distanza tra F e d.
Quando k = d(F,d)/2 l’unico punto
d’intersezione è il vertice della
parabola.
Metodo 2
Dato un punto P della
direttrice, si costruisce la
perpendicolare alla direttrice
per tale punto.
Si congiunge P con F e si
costruisce l’asse del segmento
PF.
L’intersezione delle due rette è
un punto della parabola.
Si osserva che l'asse costruito risulta tangente alla
parabola, quindi l'insieme degli assi è l'inviluppo
della parabola.
•
Selezionare il punto B (dipendente da un punto A) di cui si vuole
tracciare il luogo, quindi fare clic sul punto A per generare il luogo di
B (vedere anche il comando Luogo).
•
Note: Il punto A deve essere vincolato a un oggetto (ad es. retta,
segmento/intervallo, circonferenza).
•
Esempio:
•
•
•
•
•
Digitare f(x) = x^2 – 2 x – 1 nella barra di inserimento, quindi
premere il tasto INVIO.
Posizionare un nuovo punto A sull'asse x (vedere lo
strumento Nuovo punto; vedere il comando Punto).
Creare il punto B = (x(A), f'(x(A))), che dipende dal punto A.
Selezionare lo strumento Tool Locus.gif , quindi fare clic
prima sul punto B, poi sul punto A.
Trascinare il punto A lungo l'asse x per visualizzare
dinamicamente il movimento del punto B lungo la retta del luogo.