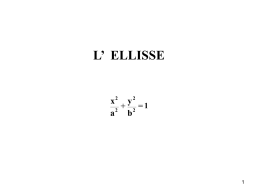Presentazione realizzata dai Proff:
• La Parabola
• L’Ellisse
• L’Iperbole
Definizione:
La parabola è il luogo geometrico di
tutti e soli i punti del piano equidistanti
da un punto fisso, detto fuoco, ed una
retta, detta direttrice.
Per costruire una parabola (1)
Per costruire una parabola
segui le seguenti istruzioni:
1) disegna una retta, la
direttrice, ed un punto ad
essa esterno, il fuoco F
2) traccia la perpendicolare
passante per F alla direttrice
(asse)
Per costruire una parabola (2)
3) determina il punto
medio del segmento
che ha per estremi F e
il punto intersezione
ottenuto
4) chiama V tale
punto, che è alla
stessa distanza da F e
dalla direttrice (V è il
vertice della parabola)
5) segna sulla
direttrice un qualsiasi
punto H
Per costruire una parabola (3)
6) traccia la
perpendicolare per H alla
direttrice
7) costruisci l'asse del
segmento HF
8) indica con P il punto di
intersezione tra questo
asse e la retta
perpendicolare per H
(come puoi notare il
punto P ha la proprietà di
essere ad uguale distanza
da F e da H)
Per costruire una parabola (4)
9) traccia il luogo che P descrive quando H si muove lungo la direttrice.
Definizione:
L’ellisse è il luogo geometrico dei punti che
hanno costante la somma delle loro distanze
da due punti detti fuochi.
L’ellisse ha due assi perpendicolari (asse
maggiore e asse minore) che sono anche assi
di simmetria.
Per costruire un’ellisse (1)
Per effettuare la costruzione dell’ellisse segui il seguente percorso:
1) disegna i due assi perpendicolari
2) facendo centro nell’intersezione degli assi disegna due circonferenze
(una più grande ed una più piccola)
3) dividi le circonferenze in tante parti uguali (più sono le parti più
preciso sarà il tracciamento dell’ellisse)
Per costruire un’ellisse (2)
4) conduci, dai punti della circonferenza più piccola, delle parallele
all’asse maggiore e, dai punti della circonferenza più grande, delle
parallele all’asse minore ottenendo così le intersezioni che individuano
i punti delle curve dell’ellisse.
Per costruire un’ellisse (3)
5) unisci tutti i punti trovati (aiutandoti con un curvilinee) ed avrai
disegnato la tua ellisse!!!
Definizione:
L’iperbole è il luogo geometrico di tutti
e soli i punti del piano per i quali è
costante la differenza delle distanze da
due punti fissi, detti fuochi.
Per costruire un’iperbole (1)
Per costruire l’iperbole segui le
seguenti istruzioni:
1) Dati due punti A e A’, traccia
l’asse del segmento AA’, passante
per il punto medio O
2) prendi sulla retta AA’, oltre A,
un punto F e il suo simmetrico F’
(rispetto ad O)
3) costruisci la circonferenza di
centro O e raggio FO
4) disegna la perpendicolare per A
al segmento AA', chiama B il punto
d'intersezione con la circonferenza
F’
A’
O
F
A
B
Per costruire un’iperbole (2)
5) traccia il segmento OB
6) traccia la perpendicolare per F
alla retta FF'
7) disegna la circonferenza di
centro A e raggio AB
8) segna il punto di intersezione
tra la retta FF' e la circonferenza
9) traccia per questo punto la
parallela al segmento OB
F’
A’
O
A
F
P’
B
10) indica con P' il punto di
intersezione di tale retta con la
retta per A e B
Per costruire un’iperbole (3)
11) individua il punto medio del
segmento P'F
12) costruisci il simmetrico P di A
rispetto a tale punto
13) quindi il simmetrico di P rispetto
ad F
14) e il simmetrico di P rispetto ad
O
15) finalmente traccia la curva
passante per P ed i suoi simmetrici
La curva costruita è
l'iperbole di fuochi F e F'
A’
F’
A
O
F
P’
P
B
Attento, se fai clic qui torni all’inizio!