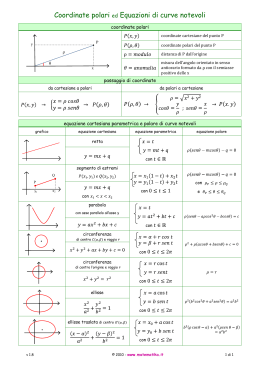
Equazione cartesiana dell’ellisse
1
Bruna Cavallaro, Treccani Scuola
Verso l’equazione dell’ellisse come luogo di punti
Animazione ‘Ellisse_Geogebra_Presenta2a’
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
2
Equazione cartesiana dell’ellisse con centro O e
fuochi sull’asse x
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
3
Tutto quello che sappiamo sull’equazione cartesiana
dell’ellisse con centro O e fuochi sull’asse x
Semiasse
minore
a!b
a, b, c sono legati dal
teorema di Pitagora:
a2 = b2 + c2
Semiasse
maggiore
Semidistanza
focale
c
Eccentricità e =
a
EQUAZIONE
x 2 y2
+ 2 =1
2
a b
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
!
4
Elementi di simmetria dell’ellisse con centro O e
fuochi sull’asse x
Semiasse
minore
Semiasse
maggiore
A, A’, B, B’ vertici dell’ellisse
EQUAZIONE
x 2 y2
+ 2 =1
2
a b
!
L’equazione rimane inalterata se:
- cambio segno all’ascissa x;
- cambio segno all’ordinata y;
- cambio segno ad x e ad y.
Perciò l’ellisse è simmetrica rispetto:
- all’asse y;
- all’asse x;
- all’origine O.
Che cosa succede se opero una simmetria rispetto alla bisettrice
del I e III quadrante, cioè se scambio x con y?
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
5
Equazione di ellisse con centro O e fuochi sull’asse y
Scambio x con y ed ecco che cosa ottengo.
Semidistanza
focale
a!b
EQUAZIONE
a, b, c sono legati dal
teorema di Pitagora:
a2 = b2 + c2
x 2 y2
+ 2 =1
2
b a
c
Eccentricità e =
a
Semiasse
maggiore
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
!Semiasse
minore
A, A’, B, B’ vertici dell’ellisse
!
6
Equazione di ellisse con centro O e fuochi su asse x o su asse y
Ecco una sintesi delle due equazioni
Animazione ‘Ellisse_Geogebra_Presenta2b’
h!k
a=h,b=k
Un’equazione del tipo
x 2 y2
+ 2 =1
2
h k
descrive un’ellisse con
centro O e fuochi su uno
degli assi cartesiani.
!
a, b, c sono legati dal
teorema di Pitagora:
a2 = b2 + c2
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
h<k
a=k,b=h
c
Eccentricità e =
a
7
Attività 2. Equazione e grafico dell’ellisse
1%&2"*33/4%&%5(/67&8/&9"#22*&3%"7&8-8/.%6%&%&"/3*)(-"-&
2"*:)-4/&3#&-;#%</*$-&-&9"%=.*&8/&-))/33->&
?/(/8-6-(/&/$&9"#22/&8/&@&A&B&2-"3*$-C&%8&*9$/&9"#22*&
(/-$-&8%6%&#$%&3.D-8%&8/&)%(*"*&8%&.*42)-6%"->&
!"#$#%&'%()*+,%-)%$#(./0%%
8
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
Che cosa abbiamo trovato
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
9
Ellissi con centro O e fuochi su uno degli
assi cartesiani
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
10
Riconoscere equazioni di ellisse con fuochi ed
eccentricità
Una simmetria rispetto alla bisettrice del I e III quadrante scambia le
ascisse con le ordinate e trasforma la curva C nella D
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
11
Risolvere problemi
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
12
Risolvere problemi
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
13
Risolvere problemi
OCM
altezza massima
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
14
Come sono stati realizzati i grafici di
ellisse di questa presentazione?
Con un software di geometria dinamica
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
15
Equazione e grafico di ellisse con un software di
geometria dinamica
Animazione ‘Ellisse_Geogebra_Presenta2c’
.
Bruna Cavallaro, Treccani scuola
16
Equazione e grafico di ellisse con un software di
geometria dinamica
Animazione ‘Ellisse_Geogebra_Presenta2c’
.
Bruna Cavallaro, Treccani scuola
17
Disegnare un’ellisse di equazione data con
un software di geometria dinamica
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
18