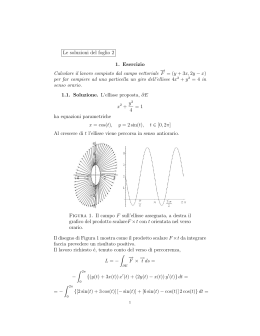
Introduzione alle coniche in coordinate polari
W
δ
A
P
ρ
V2
O
F
H
θ
R V1
D
fig. 1
Nella figura accanto è
rappresentata un’ ellisse E , il
cui fuoco destro è posizionato
nell’origine di un sistema di
riferimento polare: ρ è il
raggio vettore mentre θ è
l’anomalia.
Una conica, l’ellisse ne è un
tipo particolare, si definisce
come quella curva piana i cui
punti verificano la relazione,
con ε costante:
PF
 ,
PH
in cui se
ε = 0 si ottiene una circonferenza;
0 < ε < 1 si ottiene un’ellisse;
ε = 1 si ottiene una parabola;
1 < ε si ottiene un’iperbole.
La costante ε è chiamata eccentricità della conica, δ è chiamata direttrice della conica.
Otteniamo l’equazione in coordinate polari della generica conica, e utilizziamo , per questo la
definizione precedente

PF


=
=
,
PH
FD  FR
FD   cos
da cui, esplicitando ρ discende che
   FD   cos
 FD =    cos   1   cos 
   
 FD
.
1   cos
La grandezza costante al numeratore è generalmente sostituita da un’altra costante, la misura della
lunghezza della semicorda focale FA - chiamata anche parametro della conica - indicata con p
o con l , nel seguente modo:
    2   l =
 FD
 FD
=
=  FD . (1)
1   cos  2 1   0
Segue che la forma generale dell’equazione di una conica è:
   
l
.
1   cos
pantaprofGennaio2013/ConicheInCoordinatePolari/pagina 1 di 4
(1)
Ogni conica, per le sue caratteristiche, ha una forma particolare dell’equazione (1) . Vediamole.
Ellisse : E
Indichiamo con 2a la distanza tra i vertici V1 e V2 (O è il centro dell’ellisse). Nel sistema
polare le coordinate dei vertici sono
l
l
=
;
1   cos 0 1  
l
l
 2     
=
.
1   cos 1  
V  0, 1 
1    0  
V  ,  2 
V1V2  1   2 
l
l
1  1 
2l

l

 2a .
2
1  1 
1 
1  2
Da qui si ricava che


l  a 1  2 ,
per cui la (1) diventa
   
a 1   2 
1   cos
(2)
.
Dalla (2) si ricava che
FV1    0  
a 1   2 
1 
= a 1    ,
FV2     
a 1   2 
1 
= a 1    .
Si può riscrivere l’eccentricità nel seguente modo:
c  OF =OV1  FV1  a  a 1    = a  a   a   a ,
per cui

c
.
a
(3)
Utilizzando l’eccentricità possiamo ricavare una relazione fra i coefficienti a , b , c , dove b è la
lunghezza del semiasse minore dell’ellisse, nella fig. 1 è la misura del segmento OW . Infatti,
poiché V1 appartiene a E allora

FD a  c
ac

, per cui V1 D 
.

V1 D V1D
Anche W appartiene a E , quindi

FW
FW

,
dist W ,   OV1  V1 D
per cui
ac 
a  a  c

FW   OV1  V1D    a 
= ca c  a .
 =
 




pantaprofGennaio2013/ConicheInCoordinatePolari/pagina 2 di 4
La relazione pitagorica
2
2
2
FW  OW  OF ,
può finalmente riscriversi così
a 2  b2  c2 ,
(4)
come pure, ricordando la (3) ,
b  a 2  c 2 = a 2  a 2 2 = a 1   2 .
(5)
La (5) è valida se 1   2  0 , cioè 1    1 e quindi 0    1 , trattandosi di valori solo
positivi dell’eccentricità.
Circonferenza : C
Si ottiene dall’equazione di E se ε = 0 , quindi
   
a
 a.
1
Il parametro caratteristico è il raggio, il fuoco coincide con il centro della circonferenza, infatti
dalla (3) si ricava
c  0a  0 . (2)
Parabola : P
In questo caso ε = 1 , e l’equazione (1) diviene
   
l
.
1  cos
(6)
La P può considerarsi caso limite di E quando   1 . Infatti, poiché il parametro l
dell’ellisse diviene quello della parabola, e quest’ultimo pure è una costante - rappresenta infatti
la lunghezza costante della semicorda focale FA - allora


l  a 1   2  costante
da cui
a
l
1 1
l
.
2
1 
1  1 
Il valore di a diviene
a l
1 1 1
= l      .
1  11  1 2
Il vertice V1 dista ρ(0) = l 2 dal fuoco F , il secondo vertice dista ρ(π) = ∞ da F .
Iperbole
in fieri …
Note
(1) Si può ricavare la distanza tra il fuoco e la direttrice cioè FD  l  .
pantaprofGennaio2013/ConicheInCoordinatePolari/pagina 3 di 4
(2) La direttrice δ si trova a distanza infinita, infatti - vedi nota (1) - se l’eccentricità tende a
zero, allora il rapporto l  tende a divenire infinitamente grande, così come il segmento FD
diviene infinitamente lungo.
in fieri …
pantaprofGennaio2013/ConicheInCoordinatePolari/pagina 4 di 4