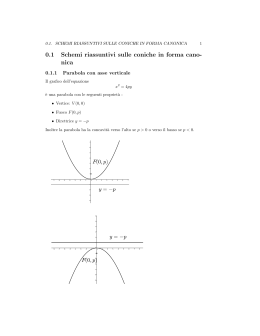
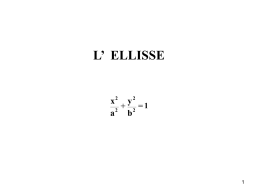LE CONICHE
Le coniche come intersezione fra un piano ed un cono matematico
CIRCONFERENZA
ELLISSE
PARABOLA
IPERBOLE
RICHIAMI SULLA RETTA
Equazione generale della retta
ax + by + c = 0
In forma esplicita y = mx+q
dove m è il coefficiente angolare
asse x
y = 0
asse y
x = 0
retta parallela all’asse x
y = k
retta parallela all’asse y
x = k
retta passante per l’origine
ax + by = 0
La Circonferenza
La circonferenza è il luogo
geometrico dei punti del piano
equidistanti da un punto fisso
chiamato CENTRO.
La sua equazione è
x  y  ax  by  c  0
2
2
r
C
Le coordinate del centro e la
lunghezza del raggio sono date da:
C( α, β) dove α = -a/2
e β= -b/2
r    c
2
2
le coordinate del centro sono sempre calcolabili, il valore invece del raggio
dipende dal fatto che il radicando sia positivo.
Nel caso in cui sia nullo, si ha una circonferenza ridotta ad un punto e raggio zero.
Se il radicando è negativo, si tratta teoricamente di una circonferenza non reale
Circonferenza e retta
Retta secante
Retta tangente
Retta esterna
Circonferenza e retta
Per trovare, nel piano cartesiano, le coordinate
degli eventuali punti di intersezione di una
circonferenza con una retta, si risolve un
sistema di secondo grado con le equazioni
assegnate
x 2  y 2  ax  by  c  0
a' x  b' y  c'  0
retta secante
se >0
retta tangente
se =0
retta esterna
se <0
L’Ellisse
Si chiama ellisse il luogo
dei punti del piano per i
quali è costante la somma
delle distanze da due
punti fissi F1 e F2
(detti fuochi).
P
F1
F2
Se F1 e F2 sono i fuochi dell’ellisse
per ogni punto P dell’ellisse si ha che:
P
PF1 + PF2 = costante
F1
F2
Consideriamo un’ellisse con centro nell’origine
e fuochi sull’asse delle ascisse.
I punti A1, A2, B1, B2
sono detti “vertici”
dell’ellisse.
A1(-a,0) A2(a,0)
B1(0,-b) B2(0,b)
B2
A1
A2
F1
A1A2 è l’ “asse maggiore”
B1B2 è l’ “asse minore”
F1F2 è l’ “asse focale”
F2
B1
F1(-c,0) F2(c,0)
dove:
c  a 2  b2
L’equazione di un’ellisse con il
centro nell’origine e i fuochi
sull’asse delle ascisse è:
x2
y2


1
a2
b2
con a > b misure dei semiassi
y
b
x
a
B2
Se i fuochi sono
sull’asse delle ordinate
si avrà un’ellisse simile
a quella in figura.
F2
A1
A2
F1
Evidentemente, l’asse
maggiore è il segmento B1B2
B1
L’equazione di un’ellisse con il
centro nell’origine e i fuochi
sull’asse delle ordinate è:
x2
a2

y2
b2
1
con b > a misure dei semiassi
c  b2  a 2
Viene chiamata eccentricità
“e” di un’ellisse il rapporto
tra la semidistanza focale
“c” e la lunghezza del
semiasse maggiore:
c
e
a
0≤e≤ 1
LA PARABOLA
y  ax  bx  c
2
La parabola è il luogo geometrico
dei punti del piano equidistanti fa
un punto fisso detto FUOCO e da
una retta fissa detta
DIRETTRICE
Se a >0 la parabola volge la
concavità verso l’alto
Se a < 0 la parabola volge la
concavità verso il basso
V è IL VERTICE DELLA PARABOLA
 b b  4ac 

V    ,

2
a
4
a


2
 b 1 b2  4ac 

F    , 

2
a
4
a
4
a


Nb.in alternativa per ricavare la y del vertice basta sostituire la
x nella equazione della parabola
Per tracciare con sufficiente precisione il
grafico di una parabola è necessario
determinarne:
•Concavità
•Vertice
•Intersezioni con gli assi cartesiani
IPERBOLE
Si chiama iperbole il luogo dei punti del piano per i quali è
costante la differenza delle distanze da due punti fissiF1 eF2
detti fuochi.
x2
y2


1
2
2
a
b
• Equazione:
x2
y2
 2  1
2
a
b
• Lunghezze degli assi:
2a asse trasverso
2b asse non trasverso
• Coordinate dei vertici: ( -a, 0 ) , ( a, 0 )
• Coordinate dei fuochi: ( -c, 0 ) , ( c, 0 )
FINE PRESENTAZIONE
G. Barbaro