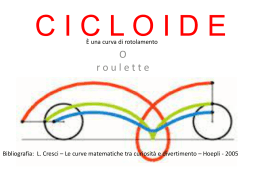
Il Giardino di Archimede Oltre il compasso 4 ALI Con filo e matita Una delle operazioni fondamentali della geometria è quella di costruire rette e cerchi. Mentre disegnare una circonferenza è relativamente facile, non è altrettanto facile disegnare una retta abbastanza precisa. Il meccanismo di Watt Nel 1784 Watt inventò un semplice meccanismo che, applicato all’asta del pistone di una macchina a vapore, lo costringeva a muoversi lungo una linea retta. Il meccanismo di Watt libero In realtà il meccanismo di Watt descrive una curva a forma di 8 con tratti quasi rettilinei, e proprio uno di questi tratti rettilinei viene sfruttato dalle macchine a vapore per compiere lavoro. Il meccanismo di ČebiČev Durante l’ottocento vennero inventati vari strumenti capaci di riprodurre un moto rettilineo, uno dei più precisi è quello di Pafnuti Lvovic Čebičev del 1850, che aveva però un moto solo approssimativamente rettilineo. Il meccanismo di Sarrus Invece nell’apparecchio di Pierre Frédérique Sarrus del 1853 la lama riusciva a muoversi verticalmente in linea retta, ma muovendosi in un ambiente tridimensionale, non era pratica. Il meccanismo di Peaucellier Quadrilateri articolati Nel 1864 Charles-Nicolas Peaucellier riuscì a rappresentare una retta sfruttando le proprietà matematiche di una trasformazione del piano: l’inversione rispetto ad una circonferenza. Questo meccanismo infatti tramite un’asta costringe il punto inerziale a muoversi su una circonferenza passante per il centro, e quindi il pennarello situato nel punto corrispondente disegna una retta. Fra i molti meccanismi di aste articolate che risolvono problemi di interesse pratico, il più semplice è il quadrilatero articolato. Il moto alternato Un quadrilatero articolato, quando una delle aste è molto più corta delle altre, può essere utilizzato per trasformare un moto alternato in un moto circolare e viceversa. Il pedale di una macchina da cucire ne è un esempio molto particolare. Le sezioni coniche Sezionando un cono, si possono ottenere tre curve diverse: un’iperbole, un’ellisse e una parabola. Possiamo disegnare un’ellisse servendosi del grande compasso tridimensionale, al quale i geometri arabi avevano dato il nome di “compasso perfetto”. L’asta inclinata descrive un cono, che viene tagliato dal piano del disegno; a seconda dell’inclinazione di quest’ultimo si ottiene una circonferenza (quando il piano è orizzontale) o un’ellisse. Se si potesse aumentare l’inclinazione del piano, si otterrebbe prima una parabola e poi un’iperbole. L’ellisse In una circonferenza tutti i punti sono alla stessa distanza dal centro. In un’ellisse il centro per così dire si sdoppia in due punti, i fuochi, e la somma delle due distanze dai due fuochi è sempre la stessa per ogni punto sull’ellisse. Questa proprietà può essere sfruttata per disegnare un’ellisse: si legano le estremità del filo ai due fuochi e si fa scorrere un pennarello tenendo i fili ben tesi. Gli specchi ustori Via via che l’ellissi si allunga, i suoi fuochi si allontanano. La parabola ha un solo fuoco, l’altro è all’infinito. Di conseguenza, i raggi luminosi che partono dal fuoco della parabola e si riflettono su di essa, diventano tutti paralleli all’asse, e viceversa. Combinando due specchi parabolici, si possono concentrare sul fuoco del secondo i raggi provenienti da una lampadina posta in quella del primo. Il calore che vi si produce può incendiare un fiammifero. La cicloide La cicloide è una curva tracciata da un punto fisso su una circonferenza che rotola lungo una retta; in pratica il disegno composto da un punto su una ruota di bicicletta in movimento. La cicloide è anche isocrona. Infatti se appoggiamo una pallina sulla cicloide e la lasciamo andare, il tempo che impiega per raggiungere il punto più basso è sempre lo stesso, quale che sia il punto di partenza. Così se facciamo oscillare una pallina su una cicloide, le oscillazioni avverranno nello stesso tempo, sia all’inizio quando sono grandi, sia quando la loro ampiezza diminuisce. Un miraggio Accoppiando due specchi parabolici in modo che il fuoco di ognuno di essi sia nel vertice dell’altro, pratichiamo un foro sullo specchio superiore e appoggiamo un dado sullo specchio inferiore. Se guardiamo in direzione obliqua attraverso il foro, dopo due riflessioni sui due specchi vediamo il dado come se fosse posto sul vertice dello specchio superiore. Il pendolo cicloidale A differenza di quanto accade per il pendolo ordinario, un pendolo che oscilla lungo una cicloide compie le sue oscillazioni sempre nello stesso tempo. L’evolvente della cicloide Se il profilo lungo cui adagiamo il filo è a forma di cicloide e il filo è lungo quanto metà della cicloide, l’evolvente è ancora una cicloide uguale alla prima. La spirale di Archimede Dopo aver messo il disco in rotazione, partiamo dal centro e muoviamo il pennarello verso l’esterno con velocità uniforme. La curva che ne risulterà è una spirale dia Archimede. Camera ellissoidale In una camera ellissoidale, le onde sonore che escono da un fuoco si riflettono sul soffitto per concentrarsi nell’altro fuoco. Infatti parlando sottovoce in uno dei fuochi della camera si viene nettamente sentiti nell’altro. Voci focalizzate Due grandi specchi parabolici permettono di comunicare a distanza: se si parla in uno dei fuochi degli specchi, la voce viene riflessa e inviata nell’altro specchio parabolico, che la concentra nel fuoco dove si sente distintamente. Video realizzato dalla 4AL liceo scientifico G. Vasari Figline Valdarno a.s. 2011/2012
Scaricare