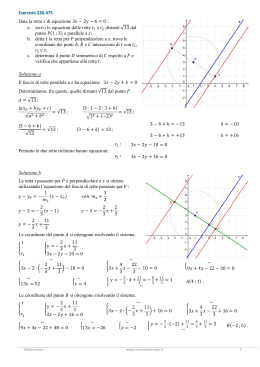
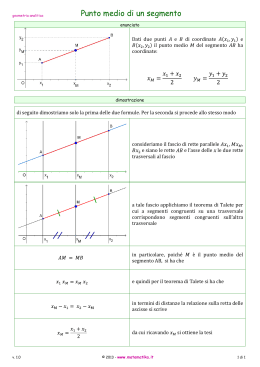
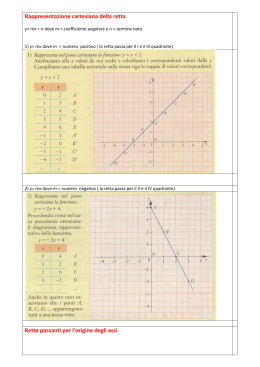
A cura di:
Alessia di Fazio
Silvia Peluso
Classe: II A TURISTICO
ITC “LIBERO DE LIBERO”
FONDI
DEFINIZIONE
• La retta è il secondo
ente fondamentale
della geometria;
geometricamente priva
di alcuno spessore ha
una sola dimensione: la
lunghezza.
TIPI DI RETTE
• ASCENDENTE, se il
coefficiente angolare è positivo.
m>0
• DISCENDENTE, se il
coefficiente angolare è negativo.
m<0
FORMA DELLE RETTE
• FORMA IMPLICITA
ax+by+c=0
• FORMA ESPLICITA
y=mx+q
m= -a/b
q= -c/b
EQUAZIONI DELLE RETTE
• PASSANTE PER
L’ORIGINE DEGLI ASSI
y=mx
• NON PASSANTE PER
L’ORIGINE DEGLI ASSI
y=mx+q
FASCI DI RETTE
• FASCIO PROPRIO
• FASCIO IMPROPRIO
Si dice proprio se ogni sua retta passa per
lo stesso punto, detto centro o sostegno del
fascio.
Un fascio proprio di rette è descritto da
un'equazione simile a quella di una retta
singola, ma in cui le costanti sono diverse.
Si dice Improprio se ogni retta è parallela
tra loro e il coefficiente angolare è
costante.
Dove q è costante.
CONDIZIONE DI PARALLELISMO E
PERPENDICOLARITÁ
• Due rette si dicono parallele
quando hanno lo stesso
coefficiente angolare.
ry=2x+1
sy=2x-1

Due rette si dicono
perpendicolari quando il
coefficiente angolare è uno
l’opposto e l’inverso dell’altro.
ry=2x+1
sy= -1/2x+1
FORMULE
• COEFFICIENTE ANGOLARE DATE
DUE COORDINATE
A(Xa;Ya)
B(Xb;Yb)
• DISTANZA DI UN PUNTO DA UNA
RETTA
ax+by+c=0
P(X0;Y0)
• EQUAZIONE DELLA RETTA
PASSANTE PER DUE PUNTI
A(Xa;Ya)
B(Xb;Yb)