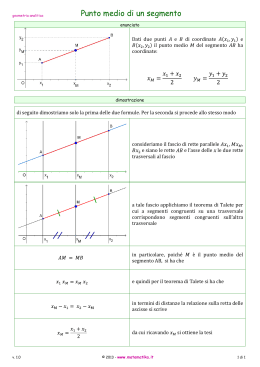
Esercizio 226.475 Data la retta di equazione 3
2
6 0:
a. scrivi le equazioni delle rette e distanti √13 dal
punto 1 ; 3 e parallele a ;
b. detta la retta per perpendicolare a , trova le
coordinate dei punti , e intersezioni di con ,
e ;
c. determina il punto simmetrico di rispetto a e
verifica che appartiene alla retta .
Soluzione a
Il fascio di rette parallele a ha equazione 3
2
0
Determiniamo, fra queste, quelle distanti √13 dal punto
.
√13 ; |
|
√13 ; √
|3
2∙3
3
|
√13 ; 2
3
|
6
|3 ∙ 1
√13 ; |3
√13
|
6
6
13
13 ; 3
∶
10
6
13
3
2
10
0
3
2
16
0
10
0 9
16
Pertanto le due rette richieste hanno equazioni:
∶
Soluzione b
La retta t passante per e perpendicolare a si ottiene
utilizzando l’equazione del fascio di rette passante per P :
1
3
2
2
3
3
1 Le coordinate del punto
2
3
2
3
2
3
2∙
13
11
3
3
4
si ottengono risolvendo il sistema:
11
3 10 0
10
52 Le coordinate del punto
9
2
3
11
3
2
3
3
2
3
3
22
2
3
2
48
0 3
22
3
4
3
4 ∙4
1 4
22
30
0
4 ; 1 .
si ottengono risolvendo il sistema:
11
3
3
16 0
0 13
26 2
3
2∙
11
3
2 0 3
16
∙
2
4
3
22
3
16
5 0 2 ; 5 .
Matematica www.mimmocorrado.it 1 Le coordinate del punto
2
3
3
9
22
4
si ottengono risolvendo il sistema:
11
3 3
6 0
2
18
0 13
2∙
40 2
3
11
3
6
0 3
4
3
22
3
∙
6
0 ;
.
Soluzione 1c
2
2
Le equazioni della simmetria centrale:
si ottengono considerando il punto
segmento
.
2
; 2
come punto medio del
; ; 2
; 2
Applicando tali formule si ottiene:
40
14
2∙1
13
13
⟹ 21 78 21 57
2∙3
13
13
13
2
2
14 57
; 13 13
Oppure sostituendo direttamente le coordinate dei punti nelle formule del punto medio:
40
40
40
14
; 1 13
; 2
; 2
13
13
13
2
2
21
21
21 78 21
; 3 13
; 6
; 6
13
13
13
2
2
Il punto
57
13
2
3
28
; 57
13
appartiene alla retta , infatti:
11
57
; 3
13
143
57
; 39
13
2
14 11
57
∙
; 3
13 3
13
171
57
; 39
13
28 11
; 39 3
57
.
13
Matematica www.mimmocorrado.it 2 Esercizio 226.476 Data la retta di equazione 3
2
2 0
determina in modo che :
a.
passi per l’origine;
b. abbia coefficiente angolare positivo;
c. sia parallela alla retta passante per 1 ; 1 ,
5 ; 7
d. abbia distanza dall’origine minore di 1;
e. formi con la direzione positiva dell’asse
un angolo compreso tra 45° e 60°.
+
Soluzione a
Calcoliamo il coefficiente angolare del fascio:
3
3
2
2
Essendo il coefficiente angolare dipendente dal
parametro , si tratta di un fascio proprio di rette.
Per determinare il centro del fascio scriviamo la sua
equazione come combinazione lineare di due rette,
raccogliendo a fattor comune il parametro :
3
2
3
2
2
∙ 1
0 ; 2
0 ;
Il centro del fascio si ottiene risolvendo il sistema fra le due rette che formano la combinazione lineare:
2
3
2 0
3 2 ; 1
1
3 2
1 2
0
2
Il fascio di rette:
 per
0
si ottiene la retta blue
3
2 0;
 per
1
si ottiene la retta nera
3
2
1 0
 per
2
si ottiene la retta verde
3
4
0
 per
∞
si ottiene la retta rossa
1 2
0;
Rappresentando queste rette si deduce che al crescere di
senso orario.
La retta del fascio 3
2
cioè
2 ⟹ 3
Soluzione b
La retta del fascio 3
0 ; 2
3
2
4
2
0 .
∈ , si ottengono rette che ruotano intorno al centro C in
0 che passa per l’origine è quella che ha termine noto nullo:
2
0 che ha coefficiente angolare positivo si ottiene ponendo
3
0 ; 0 ; 2
0 ; 0 .
2
Soluzione c
La retta del fascio richiesta deve avere coefficiente angolare uguale a quello della retta
1 7
8
2
1 5
4
2 si ha: 3
2 ; 2
2
0
0, cioè
.
Imponendo
2 ; 3
2
2 ; 3
4 ; 3
.
4
Matematica www.mimmocorrado.it 3 Soluzione d
Imponiamo che la distanza della retta del fascio 3
|
;
1 ; √
|
2|
1 ; |
2|
2
|
2
0 dall’origine sia minore di 1:
|3 ∙ 0 2 ∙ 0
2|
1 ; 3
2
1
0 ; 9
4a ; |
2|
√9
4
√9 4
√9 4
√9 4
Essendo il denominatore positivo ∀ ∈ , la frazione è negativa quando è negativo il numeratore:
|a
2|
9
4a
4a
Essendo √9
Risolviamo prima:
2
4
9
0 ; |a
2|
0 ∀a ∈ R ⟹ a
a
a
2
√9
0 ∨ 0
2
2
√9
√9
1 ; 0 ;
4a
4a
4a ; 2 0 9
2
4
2 4 4
9 4
2 2 ∨ 3
4
5 0
2 2 ∨ ∀ ∈
2 ∨ 2 a 2
∨ ∀ ∈
Cioè ∀ ∈
.
Risolviamo poi:
9
2
9
4
4
a
2
√9
4a ; 2
0 ∨ 0
2
0 9
4
2
2 4 4
4
2 2 ∨ 4
5 0
3
2 2 ∨ ∀ ∈ 2 ∨ 2
2
∨ ∀ ∈
9
Cioè ∀ ∈
.
Ritornando al sistema
a
a
2
2
√9
√9
4a
4a
si ha:
∀ ∈
∀ ∈
∀ ∈
Matematica www.mimmocorrado.it 4 Soluzione e
45°
Ricordiamo che:
1 e
60°
√3
Il coefficiente angolare del fascio è:
3
3
2
2
Occorre risolvere le disequazioni:
1
3
2
3
√3 ⟺ 2
1
√3
3
2
Risolviamo prima:
3
2
√3 ; 3
2
0 ; √3
3
2√3
2
0 ; 0 0
3
0
2
Risolviamo poi: 3
3
1
; 2
2
2
1
0 ; 0
0 3
2
2
+
- -
+
- 0 ;
3
2
0
+
- -
+ +
+
- + - 0
si ha:
∨
0 √
√3
2
X 0
Da cui si ottiene:
+ + + √3
1
√
3
2 0
Dal prodotto dei segni si ottiene: 0
Ritornando al sistema
√3
2 0
2√3 0 0 ∨ Dal prodotto dei segni si ottiene:
0
3
0
2
3
0 2√3
0 √3
2
√
Matematica www.mimmocorrado.it 5