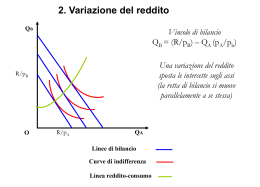
Esercitazione
•
•
•
•
•
Su di un sistema di assi cartesiani si indichino
la curva di domanda e di offerta di mercato
del bene X.
Si indichino graficamente il prezzo e la quantità
di equilibrio;
Si indichino graficamente una situazione di
eccesso di domanda e una di eccesso di offerta.
Si tracci l’effetto di un aumento di reddito dei
consumatori.
Si tracci l’effetto dell’introduzione di
un’innovazione tecnologica.
•
•
•
•
•
•
•
– Si indichino le affermazioni VERE
l’effetto di sostituzione si verifica quando il prezzo di un bene
aumenta e i consumatori tendono a sostituire il bene divenuto più
costoso con altri beni.
L’effetto di reddito indica la variazione della quantità domandata di
un bene dovuta alla variazione dei redditi reali dei consumatori
risultante dalla variazione di prezzo di quel bene.
L’elasticità della domanda rispetto al prezzo indica la variazione
percentuale della quantità domandata divisa per la variazione
percentuale del reddito.
I beni sono sostituti se un aumento del pezzo di uno determina un
incremento della domanda dell’altro.
I beni sono complementari se una diminuzione del prezzo di uno
determina una diminuzione della domanda dell’altro.
I beni sono indipendenti se una variazione del prezzo di uno non ha
alcun effetto sulla domanda dell’altro.
•
La curva di offerta di un’impresa:
– è inclinata positivamente per la presenza di
rendimenti decrescenti;
– è inclinata negativamente per la presenza di
rendimenti decrescenti;
– è il tratto crescente della curva del costo marginale
dell’impresa;
– è meno elastica della curva di domanda.
– esprime la quantità che le imprese producono per
ogni livello di prezzo.
Siano qdn=8000-1000pn e qon=-4000+2000pn
rispettivamente le curve di domanda e offerta del bene n
• Si determinino le quantità e il prezzo di equilibrio.
• L’equilibrio implica qdn=qon
8000-1000pn = -4000+2000pn
3000pn=12000
Pn=4
Sostituendo il prezzo di equilibrio nell’equazione della
domanda O dell’offerta otteniamo la quantità di equilibrio
Qdn=8000-1000(4)=4000
Q0n=-4000+2000(4)=4000
Elasticità e pendenza
• Il calcolo:
(ΔQ/Q)100/(ΔP/P)100
Dividendo numeratore e denominatore per 100 e
moltiplicando entrambi per P/ ΔP otteniamo:
ΔQ/Q x P/ ΔP
Questo è il livello al
Invertendo l’ordine dei due termini possiamo
quale si effettua la
scrivere
misurazione
ΔQ/ΔP x P/Q
Una domanda lineare
• Una curva lineare ha pendenza costante se
Δp/ Δq è costante anche il suo inverso sarà
costante. Dunque osserviamo l’elasticità
attraverso il secondo termine della formula:
p/q.
• Per che tende q a 0 il rapporto aumenta
illimitatamente da cui l’elasticità aumenta
al diminuire di q.
• Ora facciamo variare p. Spostandoci verso
destra lungo la curva di domanda p
diminuisce e q aumenta quindi il rapporto
p/q diminuisce…l’elasticità tende a
diminuire. I
In corrispondenza dell’asse delle quantità il
prezzo è nullo e dunque l’elasticità è nulla.
In corrispondenza dell’asse delle ordinate
l’elasticità è infinita.
Da cui:
• L’elasticità, nel caso di una curva di
domanda lineare, è indipendente dall’entità
e dal verso delle variazioni di p e q.
• L’elasticità è diversa dalla pendenza anche
per una curva di domanda lineare.
Una domanda non lineare
• L’elasticità, nel caso di una curva di
domanda lineare, è dipendente dall’entità e
dal verso delle variazioni di p e q.
• L’elasticità varia anche lungo una curva non
lineare….tranne il caso dell’iperbole
rettangolare.
La curva ad elasticità unitaria (spesa
costante)
•
•
Sia qdn=600/pn l’equazione della curva di
domanda del bene n.
Si calcoli la quantità domandata per il
prezzo che varia da 6 a 1:
6
5
4
3
2
1
100
120
150
200
300
600
La spesa totale
è
Sempre 600!
• Quale è il caso in cui per ogni data
variazione percentuale del prezzo la
quantità aumenta nella stessa percentuale?
E’ il caso e=1, elasticità unitaria, dunque
lungo un’iperbole rettangolare e=1 in ogni
punto!