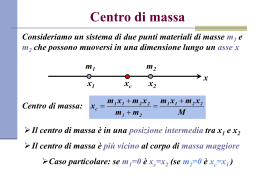
Urti




Si parla di urti quando due punti materiali interagiscono per un
intervallo di tempo estremamente breve.
si possono sviluppare forze di intensità elevata: dette “impulsive”
interne
Quando due particelle elementari ad alta energia entrano in
collisione, anche non arrivando al contatto fra loro, si tratta ancora di
urto.
Possiamo separare l’evento in tre parti: prima e dopo l’urto
(possiamo studiarne il moto) e durante
1
Urti
Sistema di particelle interagenti isolato:
Prima e dopo l’urto:
t2




m1v1,fin  m1v1,in  J 2,1   F2,1dt
t1
t2




m2 v 2,fin  m2 v 2,in  J1, 2   F1, 2 dt
t1
Impulso dovuto alla forza
esercitata da 2 su 1


J1, 2   J 2,1 




m1v1,fin  m1v1,in  m2 v 2,fin  m2 v 2,in 
Variazione della quantità di
moto della particella 1.


Pin  Pfin  costante
Principio di conservazione della quantità di moto
2
Ancora sugli urti


P1 
P2 
Se ci sono forze esterne???
La variazione della quantità di moto subita
da ciascuna particelle tra t1 e t2 sarà data da:
t2
 
t1
t2
est
F1 2  F1
 
t1
t2
dt   F
est
F21  F2
t1
1 2dt 
t2
dt   F
t1
21dt


t2
t1

t2
t1
F2est
est
F1
est
in t
est
est

est
est
in t
est
est

est
F1 dt  P1  P1  F1 2m t  F1 t  F1 2m  F1
F2 dt  P2  P2  F21m t  F2 t  F21m  F2
Se durante l’urto le forza esterna non sono impulsive e
t piccolo:
 


P2  F21m t  F12m t  P1
P1  F1 2m t
t
t
F impulsiva
Fest non
impulsiva
PT  P1  
P2  P1  P1  0

  P1
3
Urti elastici o anelastici

Dal punto di vista energetico gli urti si classificano
 Elastici: si conserva l’energia cinetica
 Anelastici: non si conserva l’energia cinetica. Può:
 diminuire (viene trasformata in altre forme di energia:
energia interna dei corpi, riscaldamento dei corpi)
 aumentare (l’energia interna dei corpi viene trasformata in
energia meccanica: esplosioni)

Urti completamente anelastici: quando i due corpi restano
attaccati dopo l’urto e non si conserva l’energia cinetica.
4
Urto completamente anelastico
5
Urto elastico
6
Sistema di riferimento del CM
Un punto di massa m1 con velocità v1 urta un punto di massa m2 inizialmente fermo.
Dopo l’urto, i due corpi si muovono attaccati. Calcolare la velocità finale dei due
corpi. Nel sistema CM quali sono le velocità dei punti prima dell’urto?
m1v1  (m1  m2 )v cm  v CM 
vi  vi  v cm
m1v1
(m1  m2 )
Prima dell’urto
v1  v1 
m1v1
m 2 v1

(m1  m 2 ) (m1  m 2 )
v2  v 2 
m1v1
m1v1

(m1  m 2 )
(m1  m 2 )
7
Sistema di riferimento del CM
  
vi  v i - v CM 
n
n


 n



P   m i vi  m i v i - m i v CM Mv CM  Mv CM  0
i 1
i 1
i 1
Nel sistema di riferimento del centro di massa la quantità di
moto totale del sistema è nulla.
..Sia prima che dopo l’urto..
8