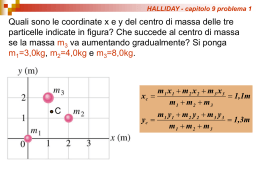
Il centro di massa di corpi simmetrici
x CM 
x
x2
x1
m 1x1  m 2x 2
m1  m 2

se m1 m 2
xCM 
x1  x2
2
• Centro di massa di una sbarra
omogenea
Asse di simmetria
Centro di
simmetria
Centro di massa
di una disco omogeneo
G.M. - Edile A 2002/03
• L’elemento oscillante di un pendolo è costituito da una sbarretta di
massa ms=0.5kg e lunga 50 cm a cui è attaccata un disco di massa
md=1kg di 20cm di diametro. Determinare la posizione del CM.
y
y
Applic
azione
• CM della sbarra (0,0.45m) ms=0.5kg
• CM del Disco (0,0.1m) md=1kg
x CM  0
x
x
m1y1  m2y 2 1kg  0.1m  0.5kg  0.45m 0.1  0.225kgm 0.325
y CM 



m  0.22m
m1  m2
1.5kg
1.5kg
1.5
G.M. - Edile A 2002/03
Il centro di massa di corpi continui
y
dm
r
x
z
n
m r
i i
rCM 
rCM 
i1
n

corp o
mi
 dm x
corp o
 dm
corp o
 dm
corp o
i1
x CM 
 dmr
y CM 
 dm y
corp o
 dm
corp o
z CM 
 dm z
corp o
 dm
corp o
G.M. - Edile A 2002/03
z
La velocità del centro
di massa
P1
• Se i vari punti materiali si muovono
• Anche il centro di massa si muoverà
• Calcoliamo la sua velocità
r1
rCM
r2
P2
r2
n
m r
i i
rCM 
m
y
r3
i1
n
P3
i
x
i1
n
 n

dri
m
r
m
i i 
i

n


dt
drCM
d i1
1 d
i1
v CM 
 
 m r  

 
dt
dt
M
M dt  i1 i i 
M


per defin izion e
perchè la deriv ata si p uò
distribuire sulla so mma


e perchè m è costan te



n
m v
i i
i1
M
i
1
perchè
è costan te
M
G.M. - Edile A 2002/03
z
L’accelerazione del
centro di massa
P1
• Possiamo anche calcolarci
l’accelerazione del centro di massa
r1
rCM
r2
P2
r2
n
m v
i i
v CM 
y
r3
i1
M
P3
x
a CM 
dv CM
dt
per defin izion e
n
 n

dvi
m
v
m
i i 
i

n


dt
d i1
1 d
i1
 
 m v  

 
dt
M
M dt  i1 i i 
M


perchè la deriv ata si p uò
distribuire sulla so mma


e perchè m è costan te



n
m a
i i
i1
M
i
1
perchè
è co stan te
M
G.M. - Edile A 2002/03
• Un’auto di massa 1000 kg è ferma ad un semaforo. Quando viene il
verde (t=0s) parte con una accelerazione costante di 4 m/s2. Nello
stesso istante sopraggiunge con velocità costante di 8m/s un camion
di massa 2000kg che sorpassa l’auto. A che distanza dal semaforo si
troverà il centro di massa del sistema autox Ccamion
 vC t per
 t=3.0s?
x C  24m
t3s
Quale sarà la sua velocità?
t=0
xa 
x
O
t=3s
O
x
x CM (3s) 
1 2
at
2
v C  vC
v a  at

t3s
x a  18m

v C  8m / s

va  12m / s
t 3s
t 3s
Applic
azione
m C x C  m a x a 2000  24  1000  18

m  22m
mC  ma
3000
m C v C  m a va 2000  8  1000  12 m
m

 9.3
mC  ma
3000
s
s
m a  ma a a 2000  0  1000  4 m
m
a CM (3s)  C C


1.33
mC  m a
3000 G.M. - Edile
s2 A 2002/03
s2
v CM (3s) 
• Un’auto di massa 1000 kg è ferma ad un semaforo. Quando viene il
verde (t=0s) parte con una accelerazione costante di 4 m/s2. Nello
stesso istante sopraggiunge con velocità costante di 8m/s un camion
di massa 2000kg che sorpassa l’auto. A che distanza dal semaforo si
troverà il centro di massa del sistema auto camion per t=3.0s?
Quale sarà la sua velocità?
Applic
azione
t=0
x
O
x CM (0s)  0m
m C vC  ma va 2000  8  1000  0 m
m
v CM (0s) 

 5.33
mC  m a
3000
s
s
a CM (0s) 
1
x CM  v CM t  a CM t 2
2
v CM (t)  v CM (0s)  at

t3s

t3s
m C a C  m a a a 2000  0  1000  4 m
m


1.3
mC  ma
3000
s2
s2
1
xCM  5.33  3  1.33  9  22.0m
2
vCM (3s)  5.33  1.33x3  9.33m / s
G.M. - Edile A 2002/03
z
Ricapitoliamo
n
m r
m x
i i
rCM =
P1
n
i i
i1
x CM =
M
r1
i1
n
rCM
r2
M
m y
i i
y CM =
i
z CM =
n
x
M
n
m v
i i
M
P3
i1
n
m v
i1
y
r3
i i
i1
v CM =
M
m z
n
m
r2
i1
n
con M 
P2
m a
i xi
vx CM =
i1
n
m a
i i
a CM =
M
n
i1
M
i xi
a xCM =
n
m v
i1
n
i yi
a yCM =
M
M
M
m a
i zi
i1
i1
n
m v
v z CM =
M
m a
i yi
vy CM =
i1
i zi
a z CM =
i1
G.M. - Edile A 2002/03
M
Il teorema del centro di massa
z
n
MaCM =

dalla definizione di
accelerazione del CM
m i ai
R (1est )
i1
mi a i  Ri
Ri  R i
( est)

F12
P1
i  1,2,..., n
f
ij
F21
r1
F13
rCM
r2
i  1,2,...,n
ji
r2
P2
R (2est )
F31
• Forze interne
– Le forze dovute alle altre
particelle che fanno parte del
sistema di punti materiali
F23
y
r3
R (3est )
P3
x
F32
• Forze esterne
– Le forze dovute alle altre
particelle che non fanno parte
del sistema di punti materiali
MaCM =
n

i1
n
m i ai 

i1

( est)
Ri 


ji

fij  

n

i1
n
R(est)

i
 f
ij
i1 ji
perchè in un a somma è po ssibile cambiareordin
l' e degli addendi
G.M. - Edile A 2002/03
Il teorema del centro di massa
z
n
R
(est)
i
R (1est )
Risultante delle forze esterne
i1
 f
ij
i1 ji
F12
P1
n
Risultante delle forze interne
F21
r1
F13
rCM
r2
• La risultante delle forze interne
è nulla
r2
F31
– Le forze interne sono a coppia
fij  fji
F23
P2
R (2est )
y
r3
– Ogni coppia ha risultante nulla
– La risultante è la somma di
tanti termini tutti nulli
R (3est )
P3
x
F32
3
 f
ij
i1 ji
 f1 2  f1 3  f2 1  f2 3  f3 1  f3 2  f1 2  f2 1  f1 3  f3 1  f2 3  f3 2  0
i1
i2
i3
0
0
0
– Il caso di n=3
G.M. - Edile A 2002/03
Il teorema del centro di massa
z
( est)
MaCM = R
•
R (1est )
L’accelerazione del centro di massa
è dovuta alle sole forze esterne.
F12
P1
F21
r1
•
•
•
•
il centro di massa si muove come un
punto materiale, avente una massa pari
alla massa totale del sistema, sottoposto
all'azione della risultante delle sole forze
esterne agenti sul sistema.
I singoli punti possono avere un moto
complicato
Il moto del centro di massa è influenzato
dalle sole forze esterne
Il moto del centro di massa rappresenta il
moto di insieme del sistema
•
F13
rCM
r2
F23
r2
F31
P2
R (2est )
y
r3
R (3est )
P3
x
F32
Il moto dell’automobile è determinato dalle forze esterne: la
forza peso, la normale esercitata dall’asfalto, la forza di attrito
esercitata dall’asfalto, la resistenza passiva offerta dall’aria
G.M. - Edile A 2002/03
z
La quantità di moto
•
P1
La quantità di moto di un sistema di
punti materiali si ottiene sommando le
quantità di moto di ciascun punto
materiale
r1
rCM
r2
P2
r2
n
P
m v
i i
i1
•
y
r3
Ricordando l’espressione della velocità
del centro di massa
P3
x
n
m v
i i
v CM 
•
i1
M to t

P = Mto tv CM
La quantità di moto di un sistema di punto materiali è
proprio uguale alla quantità di moto del Centro di Massa
– Centro di massa:
• massa pari alla massa totale del sistema
• velocità uguale alla velocità del centro di massa
Per quanto riguarda la
quantità di moto, il centro
di massa rappresenta
completamente il sistema di
particelle.
G.M. - Edile A 2002/03
I equazione cardinale della dinamica dei
sistemi di punti materiali
dP dMto tv CM 
dv
(e)
=
 Mto t CM  Mto ta CM  R
dt
dt
dt
teorema del cen tro di massa
z
dP
= R(e)
dt
•
•
•
La derivata della quantità di moto di un
sistema di punti materiali
è uguale alla risultante delle sole forze
esterne
P1
r1
rCM
r2
È equivalente al teorema del centro di massa
P2
r2
y
r3
P3
x
G.M. - Edile A 2002/03
La conservazione della quantità di moto
•
Se la risultante delle forze esterne è nulla
dP
=0
dt
•
•
•

P  costante
la quantità di moto delle singole particelle agenti sul sistema possono
variare, ma la quantità di moto totale del sistema rimane costante in
modulo, direzione e verso.
Un sistema isolato è un sistema molto lontano da altri corpi e quindi non
soggetto a forze esterne: la quantità di moto di un sistema isolato si
conserva.
La conservazione della quantità di moto è equivalente alla terza legge di
Newton
dP dp1 dp2


0
dt
dt
dt

dp1
dp
 2
dt
dt

f12 = -f21
Noi abbiamo ricavato la conservazione della quantità di moto dalle leggi di Netwon: in realtà il principio
di conservazione della quantità di moto è un principio più generale: vale anche al di fuori della
meccanica classica.
G.M. - Edile A 2002/03
•
Un’astronave di massa totale M sta viaggiando nelle profondità dello spazio
con una velocità vi=2100km/h rispetto al sole.
Espelle uno stadio posteriore di massa 0.20M alla velocità relativa
u=500km/h rispetto all’astronave, diretta lungo l’asse x.
Quanto diventa la velocità dell’astronave rispetto al sole?
Applic
azione
Indichiamo con U la velocità dello
stadio posteriore rispetto al sole.
Siamo molto lontani da qualsiasi altro
corpo, quindi le forze esterne sono nulle.
La quantità di moto si conserva.
Consideriamo il sole come un sistema di
riferimento inerziale
dP
=0
dt

P  costante
Pi  Pf
La quantità di moto iniziale è diretta lungo l’asse x
La quantità di moto finale dello stadio posteriore è anch’essa diretta lungo l’asse x
Anche la quantità di moto del resto dell’astronave sarà diretta lungo l’asse x
Pix  Pfx  Mv i  0.20M  U  0.80M  vf
Mvi  0.20M  v f  u  0.80M  vf
v  v' vO'
U  u  v f
 Mvi  Mvf  0.20Mu
km
km
v f  v i  0.20u  2100 km
h  0.20  500 h  2200 h
G.M. - Edile A 2002/03
La conservazione parziale della quantità
di moto
• La I equazione cardinale della dinamica dei sistemi è una relazione
vettoriale
dP
= R(e)
dt
• Se il sistema non è isolato, allora la risultante non sarà nulla
– È possibile che alcune delle componenti della risultante siano nulli
– Allora si conservano le corrispondenti componenti della quantità di moto
dP
(e)
=R
dt

dPx
= R(ex )
dt
dPy
(e )
= Ry
dt
dPz
= R(e)
z
dt
R (e)
x  0

Px  costante
 Ry  0
R (e)
z  0


Py  costante
Pz  costante
(e)
G.M. - Edile A 2002/03
•
Nella figura si vede un vagone ferroviario a pianale basso di massa M che è
libero di muoversi senza attrito su un binario rettilineo orizzontale.
Applic
All’inizio un uomo di massa m sta fermo sul vagone che viaggia verso destra
azione
con velocità vo. Quale sarà la variazione di velocità del vagone se l’uomo si
metterà a correre verso sinistra con una velocità vrel rispetto al vagone?
Si assuma vo=1m/s, vrel=5m/s, m=70kg, M=1000kg.
In questo caso le forze esterne non sono nulle:
peso del vagone, peso dell’uomo, reazione
vincolare del binario (solo componente
normale).
Però le forze sono tutte verticali
Si conserva la quantità di moto orizzontale, in
x
particolare quella diretta secondo i binari.
Il sistema di riferimento è quello dei
binari (inerziale).
Pix  Pfx
dPx
= R est
x =0
dt

Px  costante
 M  m vi  mv u  Mv f vu velocità dell’uomo rispetto ai binari
Dai moti relativi
v  v' vO'
v u  v rel  v f
M  mvi  m  vf  v rel   M  vf  M  mv i  M  mv f  mv rel
vf 
mM
m
70 m 1140
vi 
v rel  1 ms 
5 
mM
m M
1070 s 1070
m
s
 1.07 ms
G.M. - Edile A 2002/03
Urti
• Si parla di urti quando due punti materiali (o due sistemi di punti
materiali) si scambiano energia e quantità di moto in un tempo
estremamente breve.
p
Fm 
t
p la variazione di quantità di moto è finita
t tende a zero
• Le forze agenti sulle particelle interagenti sono estremamente intense
(forze impulsive!!)
G.M. - Edile A 2002/03
Fasi dell’urto
• fase iniziale prima dell’urto: in cui esiste un moto imperturbato.
• fase dell’urto:
– La durata di questa fase è piuttosto piccola rispetto alla
durata complessiva del moto.
– Si produce quindi una brusca variazione nel moto dei due
sistemi interagenti
– È caratterizzata dalla presenza di forze molto intense.
r  vt
 r  0
t  0
Poiché l’urto è istantaneo,
le particelle, nella fase
dell’urto, non si spostano.
• fase successiva all'urto: dopo l'interazione, lo stato di moto continua ad
essere di nuovo imperturbato.
Il CM si trova sempre sul segmento che congiunge le
due particelle. L’urto avviene nel CM
G.M. - Edile A 2002/03
Impulso della forza
• Durante l’urto le forze che agiscono sulle
particelle interagenti hanno una intensità molto
grande (tendente all’infinito).
F21
F12
1 2
F12
– Sono difficili da descrivere.
– Quello che è importante è l’effetto prodotto
• Consideriamo una delle due particelle interagenti
F12m
– La particella 1
– La sua variazione di quantità di moto, prodotta
dalla forza F12, vale: p  p  p
1
1f
1i
t2
t1
• Si definisce Impulso della forza F12 la quantità:
dp1
 F1 2
dt
dp1  F1 2dt  p1 

t2
dp1 
t1

t2
F1 2dt
t1
t
I1  p1  p1f  p1i
I1 
La stessa variazione di quantità di moto può essere ottenuta con una forza
molto intensa che dura molto poco,
o da una forza meno intensa che agisce per un tempo piu lungo.

t2
F1 2dt
t1
Rappresentato
dall’area sotto
la curva
G.M. - Edile A 2002/03
Forza media
• La forza media è la forza costante che, agendo
nell’intervallo tra t1 e t2, provoca la stessa
variazione di quantità di moto della forza F12:
P1 
t2
F21
F12
1 2
F12
 F dt  F
t1
12
1 2m t
F12m
L’impulso in questo caso è rappresentato
dall’area del rettangolo di base t e
altezza F12m
t1
t2
t
l’area del rettangolo di base t e altezza
F12m è uguale all’area sotto la curva
dell’intensità della forza in funzione del
tempo
G.M. - Edile A 2002/03
•
Una pallottola da 30 g, con velocità iniziale di 500 m/s penetra per 12 cm in
una parete di muratura prima di fermarsi
Di quanto si riduce l’energia meccanica della pallottola?
Qual è la forza media che ha agito sulla pallottola mentre penetrava nella
parete?
Quanto tempo ha impiegato la pallottola per fermarsi?
Prima
Usiamo il sistema di riferimento del Laboratorio
per descrivere il moto:
la parete è ferma in tale sistema
il sistema di riferimento è inerziale
Le forze agenti sono:
La forza peso (fa lavoro nullo)
La Normale (fa lavoro nullo)
La forza di attrito(dinamico)
Applic
azione
x
Dopo
L’energia meccanica totale coincide con
l’energia cinetica.
Nell’ipotesi di un moto orizzontale come
mostrato in figura, non c’è variazione
dell’energia potenziale della forza peso
Kf  0
1
1
1 2
E  K f  Ki   mv 2i    30  103  5002  3750J
K i  mv i
2
2
2
E
3750
3
P

mg

30

10
 9.81  .294N
E  Wnc  Fx x  Fx 


31250N
2
x 12  10
E  Ef  Ei  Kf  Ki
Circa 100 mila volte il peso
G.M. - Edile A 2002/03
• Per calcolaci tempo ha impiegato dalla pallottola per fermarsi,
valutiamo l’impulso della forza.
Prima
I  p  pf  pi
Applic
azione
x
La quantità di moto finale è nulla
Quella iniziale ha solo la componente x
Anche l’impulso avrà solo la componente x
Dopo
I x  p x f  px i  mv i  30  10 3  500  15kgms 1
I x  Fx t  t 
Ix
15

 0.032s
Fx 31250
Il proiettile impiega 3.2 centesimi di secondo per fermarsi
Questo semplice esempio mostra come
le forze negli urti siano molto intense
I tempi dell’interazione siano piuttosto piccoli
G.M. - Edile A 2002/03
Soluzione dei problemi di urto
Sistema isolato
• Consideriamo dapprima un urto, in
cui le particelle interagenti sono così
lontane da altre particelle da poter
considerare nulle le forze esterne
(sistema isolato)
• Dalla I equazione cardinale dei
sistemi ricaviamo che la quantità di
moto totale del sistema di particelle
interagenti si deve conservare.
dP
 R est  0  P  cos t
dt
F21
F12
1 2
Sistema delle particelle
interagenti
P  p1  p2  cos t
p1i  p2 i  p1f  p2 f
 p2 f  p2i  p1f  p1i

p1  p2
I1  I2
G.M. - Edile A 2002/03
Soluzione dei problemi di urto
in presenza di forze esterne
• Consideriamo ora il caso in cui le
F21
F12
particelle interagenti durante l’urto sono
est
F
1 2
1
sottoposte anche ad alcune forze esterne.
F2est
• La variazione della quantità di moto
Sistema delle particelle
subita da ciascuna particelle tra t1 e t2
interagenti
t2
t2
t2
sarà F
da:
est
est
in t
est
est
est
P1 

F
dt

F
dt

F
dt

P

P

F
t

F
t

F

F
data


12
1
12
1
1
1
1 2m
1
1 2m
1 t

P   F
t1
t2
2
t1
21
 F2
est


dt   F dt  
t1
t2
t1
21
t1
t2
t1
est
in t
est
Se durante l’urto la forza esterna è trascurabile rispetto a
quella interna
P1  F1 2m t
P2  F2 1m t  F1 2m t  P1
P  P1  P2  P1  P1  0
 P1

F2 dt  P2  P2  F21m t  F2 t  F21m  F2
Bisogna assicurarsi
che le forze esterne,
durante l’urto non
diventino impulsive
est
est
t
F12
F12m
F1est
t2 2002/03t
t1 G.M. - Edile A
Forze esterne impulsive
• Quali forze mi possono dare fastidio?
• Quali forze durante l’urto possono diventare impulsive?
• Tutte quelle forze per cui non abbiamo travato una espressione per
calcolare il loro valore!
• Forze che conservano una intensità finita durante l’urto:
–
–
–
–
Forza peso
Forza elastica
Gravitazione universale
Resistenza passiva
P  mg
Felx  kx
mM
FG 2
r
F   bv
• Forze che possono diventare impulsive durante l’urto:
– Componente normale della reazione vincolare N
– Forze di attrito (attraverso il loro legame con la normale N)
– Tensione nelle funi
G.M. - Edile A 2002/03
Conservazione della quantità di moto
• Se le forze esterne sono nulle o trascurabili rispetto a quelle impulsive
interne
• Si conserva la quantità di moto del sistema delle particelle interagenti.
P  0  Pi  Pf
P1i  P2i  P1f  P2 f
m1v1i  m2v 2i  m1v1f  m2v 2f
m 1v1x i  m 2v 2x i  m1v1x f  m 2v 2x f
m 1v1y i  m 2v 2y i  m1v1y f  m 2v 2y f
2
1
F21
F12
m1v1zi  m 2 v2 zi  m1v1zf  m 2 v2 zf
• Conoscendo le velocità iniziali, si
possono determinate le velocità
delle particelle dopo l’urto?
• 3 equazioni con 6 incognite
v2
v1
1 2
v’1
1
v’2
2
Sistema delle particelle
interagenti
G.M. - Edile A 2002/03
Istante iniziale e finale nello studio dei
processi d’urto
• Se le forze esterne sono assenti allora
– Le due particelle sono sottoposte solo all’azione delle forze interne che
esistono solo durante l’urto.
– Sia prima che dopo l’urto non sono soggette a forze: si muovono di moto
rettilineo uniforme, con quantità di moto costante.
– i e f possono essere due istanti qualsiasi prima e dopo l’urto.
• In presenza di forze esterne invece
– i e f devono essere l’istante immediatamente
prima dell’urto e quello immediatamente dopo
l’urto.
– Se si allunga l’intervallo di osservazione
• La variazione della quantità di moto prodotta
dalla forza esterna potrebbe non essere più
trascurabile rispetto a quella prodotta dalla
forza interna.
• Non c’è più conservazione della quantità di
moto
G.M. - Edile A 2002/03
Moto del centro di massa in un processo
d’urto
• Se nell’urto si conserva la quantità di moto
• Il centro di massa si muove con velocità
costante:
P  Mv CM
P  costante


v CM  costante
• Il Sistema di riferimento del CM è un sistema
di riferimento inerziale
– Molto utile per risolvere i problemi d’urto.
G.M. - Edile A 2002/03
Conservazione parziale della quantità di
moto
• Se tra le forze esterne agenti sulle particelle che si urtano c’è una forza
che, durante l’urto potrebbe diventare impulsiva (reazione vincolare,
tensione, etc)
• Non è lecito applicare la conservazione della quantità di moto.
• In alcuni casi però è possibile stabilire a priori la direzione della forza
impulsiva
• Vuol dire che si conserveranno le componenti della quantità di moto
nelle direzioni perpendicolari a quella della forza impulsiva
R est
x  impulsiva
est
R est
y  0 Rz  0
dP
est
R

dt
dPx
 R est
Px potrebbe non conservarsi
x (impulsiva ) 
dt
dPy
est
 Ry  0
 Py si conserva
dt
dPz
 Rzest  0
 Pz si conserva
dt
G.M. - Edile A 2002/03
Urti elastici o anelastici
• Dal punto di vista dell’energia gli urti si classificano
– Elastici
• Se l’energia cinetica si conserva
– Anelastici
• Quando non si conserva l’energia cinetica
•
Nota Bene: Solo l’energia cinetica è importante. Infatti:
– Se non ci sono forze esterne non c’è energia potenziale
– Comunque durante l’urto la posizione delle particelle non varia, non
varia neppure l’energia potenziale.
r  vt
 r  0
t  0
• Nel caso di urti anelastici, l’energia cinetica può
– sia diminuire (viene trasformata in altre forme di energia: energia
interna dei corpi, riscaldamento dei corpi)
– ma anche aumentare (l’energia interna dei corpi viene trasformata
in energia meccanica: esplosioni)
•
Urti completamente anelastici
N.B. non c’è alcuna
correlazione tra la
conservazione
dell’energia e quella
della quantità di moto
– Quando viene persa tutta l’energia cinetica che è possibile perdere
compatibilmente con la conservazione della quantità di moto.
G.M. - Edile A 2002/03
Urti completamente anelastici
• Sono quegli urti in cui si perde tutta l’energia cinetica che è possibile
perdere compatibilmente con la conservazione della quantità di moto
P  Mv CM
P  cost

vCM  cost
1
1
K' = m1v' 21  m 2v' 22
2
2
K'  0
Per il teorema di Konig
1
K  Mv 2CM  K'
2
dove K' è l' energia cinetica
misurata nel sistema del CM
v' 1  0

v' 2  0
se vCM  cost

al più K' può annullarsi
1
1
K' = m1v' 21  m 2v' 22
2
2
• Le due particelle nello stato finale hanno
velocità nulla rispetto al centro di massa
• Poiché al momento dell’urto, entrambe
le particelle si trovavano nella posizione
del centro di massa
• Le due particelle emergono dall’urto
unite insieme e si muovono con la
G.M. - Edile A 2002/03
velocità del CM
Soluzione dell’urto completamente
anelastico
• Consideriamo un urto completamente anelastico in cui si conserva la
quantità di moto (non ci sono forze esterne impulsive)
m1v1i  m2v 2i  m1v1f  m2v 2f
• A cui possiamo aggiungere l’ulteriore condizione: v1f  v 2f  v f
m1v1i  m2v 2i  m1  m2 v f
vf 
m1v1i  m 2 v2 i
m1  m2
• Abbiamo tre equazioni con tre
incognite
– Il problema ammette soluzione
• Velocità del
CM
G.M. - Edile A 2002/03
Il pendolo balistico
• Veniva usato per misurare la velocità dei proiettili sparati da un’arma
da fuoco.
• Consiste in un blocco di legno (o sacco di sabbia)
appeso al soffitto con una corda di lunghezza l
• Il proiettile penetra nel blocco di legno e si ferma
rispetto al blocco (l’urto è completamente anelastico)
• Blocco e proiettile, insieme, dopo l’urto
cominceranno ad oscillare come un pendolo
• Misurando l’ampiezza delle oscillazioni, dalla
conoscenza degli altri parametri in gioco, massa del
blocco, massa del proiettile e lunghezza del pendolo,
è possibile risalire alla velocità iniziale del proiettile
O
m
v
M
G.M. - Edile A 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di lunghezza
L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con esso.
Determinare la perdita di energia meccanica nell’urto.
Determinare l’elongazione massima del pendolo
Se la pallottola è penetrata nel pendolo per un tratto di 3cm, stimare la forza
media che ha frenato la pallottola rispetto al blocco e la durata dell’urto
Verificare che lo spostamento subito dal pendolo durante l’urto è trascurabile.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
Applic
azione
O
m
v
M
G.M. - Edile A 2002/03
Il pendolo balistico: analisi delle forze
•
•
•
•
Le forze peso non sono impulsive
La tensione potrebbe diventare impulsiva durante l’urto.
Non possiamo imporre la conservazione della quantità di
moto
Poiché l’urto dura poco, la posizione del pendolo durante
l’urto non varia
O
T
m
– Il filo durante l’urto resta verticale
•
•
•
Tutte le forze esterne durante l’urto sono verticali
Si conserva la componente della quantità di moto
orizzontale.
P1xi  P2xi  P1xf  P2xf
In particolare:
mv  M  mVx
Pm
v
M
x
PM
mv
Vx 
M m
G.M. - Edile A 2002/03
Energia persa nell’urto
Ki 
1
mv 2
2
2
1
1
1 m 2 v2
 mv 
2
K f  M  mVx  M  m 

M  m 
2
2
2M m
Vx 
mv
M m
1
 m 
2  m

K f  mv
 Ki
M  m 
M  m 
2
mino re di 1
K persa  Ki  K f 
1
1
m  1
 m  1
2 
2  M 
mv 2  mv 2 

mv
1

mv
 M  m  2
M  m 
2
2
M  m  2
se m<< M questo
termine è 1
Quasi tutta l’energia cinetica viene persa durante l’urto a causa delle forze di
attrito che si oppongono alla penetrazione del proiettile nel blocco di legno.
K  K f  Ki   Kp ersa  Wfa  Fa x
Il lavoro della altre forze agenti o è
nullo o è trascurabile
x = penetrazione
G.M. - Edile A 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di
lunghezza L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con
esso.
Determinare la perdita di energia meccanica nell’urto.
Determinare l’elongazione massima del pendolo
Se la pallottola è penetrata nel pendolo per un tratto di 3cm, stimare la forza
media che ha frenato la pallottola rispetto al blocco e la durata dell’urto
verificare che lo spostamento subito dal pendolo durante l’urto è trascurabile.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
mv
30  10 3 kg  500 m s
Vx 

 3.72 m s
M m
4.030kg
1 2 M
1
4.
mv
 30  10 3  500 2

2
M m 2
4.030
 3750  .993  3696.0J
Applic
azione
O
K persa 
m
v
M
K  K f  Ki   Kp ersa  Wfa  Fa x
Kp ersa
3696.0
Fa 

 123201N
x
3  10 2
p1f  p1i 30  1033.72  500
t 

 0.12  10 3 s
Fax
123201N
d  Vx t  3.72 m s  .12  10 3 s  .44  10 3 m
G.M. - Edile A 2002/03
II fase oscillazione
• L’oscillazione avviene sotto l’azione della forza peso
(conservativa) e della tensione.
E  Wn c  WT
O

h  (1 cos)
T
U f  M  mgh  M  mg (1 cos)
h
dr
M +m
Ei  Ef
PM m
Ki  U i  Kf  U f
1
M  m Vx2  0  0  M  m g 1  cos 
2
1 m 2v 2
 M  m g 1  cos 
2 Mm
v
Vx 
mv
M m
M m
2g 1  cos 
m
G.M. - Edile A 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di
lunghezza L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con
esso.
Determinare la perdita di energia meccanica nell’urto.
Determinare l’elongazione massima del pendolo
Se la pallottola è penetrata nel pendolo per un tratto di 3cm, stimare la forza
media che ha frenato la pallottola rispetto al blocco e la durata dell’urto
Verificare che lo spostamento subito dal pendolo durante l’urto è trascurabile.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
mv
30  10 3 kg  500 m s
Vx 

 3.72 m s
M m
4.030kg
Applic
azione
O
Ei  Ef
Ki  U i  Kf  U f
1
M  m Vx2  0  0  M  m g 1  cos 
2
 1 Vx2   1 3.722 
  1 
 .6473
cos   1
 2 g   2 9.81  2 
m
v
M
  ar cos.6473  50
G.M. - Edile A 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di
lunghezza L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con
esso.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
y
Prima dell’urto:
T  P  0  T  P
Applic
azione
O
T  Mg  4  9.81  39.24N
Subito dopo l’urto, il pendolo è rimasto nella stessa
posizione, ma si sta muovendo con velocità Vx:
m
v
M
T  P  M  ma
Proiettando su un asse verticale:
T  M  m g  M  m 
T  M  m g  M  m 
Vx2
Vx2
2

3.72


  46.45N
 4.030 9.81 

2 
G.M. - Edile A 2002/03
Proiettile sparato dall’alto
• La forza FMn è impulsiva (forza interna)
• Poiché la lunghezza della corda ideale non varia
m
O
v
T  PM  FMm  Ma  0
M
T  Mg  FMm  0  T  Mg  FMm FMm
• La tensione T ha, durante l’urto, una intensità
comparabile con la forza FMn
• La tensione T è impulsiva
• Se la corda non è sufficientemente robusta si può
rompere (viene superato il carico di rottura)
• Non si ha conservazione della quantità di moto
nella direzione verticale
x
T
M
FM m
PM
G.M. - Edile A 2002/03
Urto in due dimensioni
• Consideriamo un urto in cui una della due
particelle è ferma (senza forze esterne)
– Particella 1 proiettile
– Particella 2 bersaglio
– b parametro d’urto
v1
m1
b
m2
• La retta di azione della velocità v1 e il punto P2
definiscono un piano
– Le forze di interazione sono lungo la congiungente
– Quindi contenute nel piano
– Non c’è moto perpendicolarmente al piano
precedentemente individuato (accelerazione nulla,
velocità iniziale nulla)
P1i  P2 i  P1f  P2 f
y
• L’urto è piano.
v' 1
m1v1  m1v' 1 cos1  m2 v' 2 cos2
0  m1v' 1 sen1  m2 v' 2 sen 2
Se l’urto è elastico
si può aggiungere:
1
1
1
m1v21  m1v' 12  m 2 v' 22
2
2
2
1
v1
m1
m2
x
2
v' 2
G.M. - Edile A 2002/03
Urto in una dimensione -Urto centrale
• L’urto centrale avviene quando il parametro d’urto
b è nullo.
– Le forze sono dirette lungo la congiungente delle
due particelle
– Che coincide con la retta di azione della velocità
iniziale
• Non essendoci forze perpendicolari alla direzione
della velocità, non ci saranno accelerazioni
perpendicolari alla velocità iniziale
– Siccome la velocità iniziale ha solo componenti
lungo la retta congiungente i due punti materiali
– Non ci sarà moto perpendicolarmente alla
congiungente le due particelle
• L’urto centrale è un urto unidimensionale.
v1
m1
m2
b
Urto centrale
v1
P1i  P2 i  P1f mP22 f
m1
x
m1v1x  m1v' 1x m2 v' 2x
Una sola equazione non basta per determinare le due velocità dello stato finale.
Se l’urto è elastico si può aggiungere:
Nel caso di urto elastico
abbiamo due equazioni
1
1
1
m1v21x  m1v' 21x  m 2 v' 22x
indipendenti in due incognite:
2
2
2
Il sistema ammette G.M.
soluzione
- Edile A 2002/03
Urto centrale elastico-bersaglio fermo
• Per risolvere il sistema conviene metterlo in questa
forma:
m 1v1x  m 1v' 1x m 2 v' 2 x
1
1
1
m1v21x  m1v' 21x  m 2 v' 22x
2
2
2
Urto centrale
v1
m 1v1x  v' 1x   m 2 v' 2 x
2
m 1 v1x
 v' 21x  m 2 v' 22 x

P1i  P2 i  P1f mP22 f
m1

x
• Dividendo membro a membro la seconda per la prima:
m 1v1x  v' 1x   m 2 v' 2 x
v1x  v' 1x  v' 2 x


v1x  v' 1x  v' 2 x
m 1  m 2 
m 1  m 2 

m  m 2 
v1x  v1x  1
  v' 2 x

m1  m 2 
v' 1x  v1x

m 1v1x  v' 1x   m 2 v1x  v' 1x

v' 1x  v1x
m 1  m 2 
m 1  m 2 
v' 2 x  v1x
2m 1
m1  m 2 
v1x m1  m 2   v' 1x m1  m 2 
v1x  v' 1x  v' 2 x
G.M. - Edile A 2002/03
Urto centrale elastico: casi particolari
m 1  m 2 
v' 1x  v1x
m 1  m 2 
Urto centrale
2m 1
v' 2 x  v1x
m1  m 2 
v1
• La particella bersaglio, dopo l’urto si muoverà
sempre nello stesso verso della particella incidente
• La particella proiettile invece
procede nello stesso verso che aveva prima dell'
procede in verso opposto a quello che aveva prima dell'
P1i  P2 i  P1f mP22 f
m1
x
urto se m1  m 2
urto se m1  m 2
si ferma
se m1  m 2
• In caso di forti asimmetrie:
m 1  m 2

v' 1x  v1x
m1  m2
m
 v1x 1  v1x
m1  m2
m1
m 1  m 2

v' 1x  v1x
m1  m2
m 2
 v1x
 v1x
m1  m2
m2
v' 2 x  v1x
2m1
2m1
 v1x
 2v1x
m1  m 2
m1
v' 2x  v1x
2m 1
2m1
 v1x
0
m1  m 2
m2
G.M. - Edile A 2002/03
•
•
•
Due automobili A e B di massa rispettivamente 1100 kg e 1400 kg, nel
tentativo di fermarsi ad un semaforo, slittano su una strada ghiacciata. Il
coefficiente di attrito dinamico tra le ruote bloccate delle auto e il terreno è
0.13. A riesce a fermarsi, ma B che segue, va a tamponare il primo veicolo.
Come indicato in figura, dopo l’urto A si ferma a 8.2 m dal punto di impatto e
B a 6.1 m. Le ruote dei due veicoli sono rimaste bloccate durante tutta la
slittata.
Determinare le velocità delle due vetture subito dopo l’impatto.
E la velocità della vettura B prima dell’urto.
Applic
azione
K  WP  WN  WFa  WFa
0
WFa  Fax  mg x
1
K f  Ki  0  mv 2  mgx
2
N
v  2gx
v A  2  0.13  9.81  8.2  4.6 m s
v B  2  0.13  9.81  6.1  3.9 m s
m B vo  m B vB  m A v A
 vo 
P
Fa
m B vB  m A vA 1400  3.9  1100  4.6

 7.5 m S
mB
1400
G.M. - Edile A 2002/03
Urto centrale elastico-bersaglio mobile
•
•
In questo caso sia la velocità della particella 1 che quella
della particella 2 sono dirette lungo la congiungente le due
particelle.
Considerando le componenti delle velocità lungo l’asse x:
m1v1x  m2 v2x  m1v' 1x m2 v' 2x
1
1
1
1
m1v21x  m 2 v22 x  m1v' 21x  m 2 v' 22x
2
2
2
2
•
Urto centrale
v1
v2
x
P1i  P2 i  P1f mP22 f
m1
m 1v1x  v' 1x   m 2 v' 2x v 2x 



2
m 1 v1x
 v' 21x  m 2 v' 22x v 22x

Operando come nel caso precedente, dividendo membro a membro la
seconda per la prima si perviene al seguente risultato:
v' 1x  v1x
m1  m 2
2m 2
 v2 x
m1  m 2
m1  m2
v' 2 x  v1x
2m1
m  m1
 v2 x 2
m1  m2
m1  m 2
•
Se le particelle hanno la stessa
massa, nell’urto si scambiano le
velocità
m1  m2
v' 1x  v2 x

v' 2 x  v1x
G.M. - Edile A 2002/03
•
Un blocco di massa m1=2.0 kg scivola su di un piano privo di attrito alla
velocità di 10 m/s. Davanti a questo blocco, sulla stessa linea e nello stesso
verso, si muove a 3.0 m/s un secondo blocco, di massa m2=5.0kg. Una molla
priva di massa , con costante elastica k=1120 N/m, è attaccata sul retro di m2.
Qual è la massima compressione della molla quando i due blocchi si urtano?
Quali sono le velocità finale dei due corpi dopo l’urto.
•
•
•
–
–
–
–
Applic
azione
Quando la molla è alla sua
massima compressione i due
blocchi sono fermi uno rispetto
all’altro
Prima della massima compressione si sono avvicinati
Successivamente si allontanano
La velocità comune dei due blocchi sarà uguale a quella del centro di massa
Poiché la quantità di moto si conserva, anche la velocità del centro di massa sarà
uguale a quella iniziale:
m v  m 2 v2 2.0  10  5.0  3 35.0
v' 1  v' 2  vCM  1 1


 5ms
m1  m2
7.0
7.0
– La differenza tra l’energia cinetica iniziale e quella finale è
immagazzinata come compressione della molla
m1v12  m2 v 22  m1  m2 v 2CM
1
1
1
1
x 
m1v21  m 2v 22  m1  m 2 v2CM  k x 2
k
2
2
2
2
G.M. - Edile A 2002/03
•
•
•
Un blocco di massa m1=2.0 kg scivola su di un piano privo di attrito alla
velocità di 10 m/s. Davanti a questo blocco, sulla stessa linea e nello stesso
verso, si muove a 3.0 m/s un secondo blocco, di massa m2=5.0kg. Una molla
priva di massa , con costante elastica k=1120 N/m, è attaccata sul retro di m2.
Qual è la massima compressione della molla quando i due blocchi si urtano?
Quali sono le velocità finale dei due corpi dopo l’urto.
Applic
azione
– Da cui
x 
m1v12  m2 v 22  m1  m2 v 2CM
k
x 
2  100  5  9  7  25
70
1
1


  .25m
1120
1120
16 4
– Utilizzando le espressioni per l’uro centrale elastico:
v' 1x  v1x
v' 2 x  v1x
m1  m 2
2m 2
3
10
 v 2x
 10
 3.0
 0 ms
m1  m 2
m1  m 2
7
7
2m 1
m  m1
4
3 49
 v 2x 2
 10  3.0 
 7ms
m1  m 2
m1  m 2
7
7
7
G.M. - Edile A 2002/03