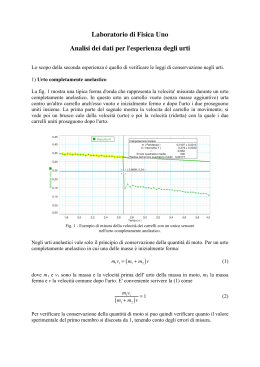
Quantità di moto
• La quantità di moto (o momento lineare) di un corpo di massa m che si
muove a velocità v è il vettore
p= mv
La quantità di moto è il prodotto di uno scalare m e di un vettore v, quindi è un vettore
che ha:
– stessa direzione e stesso verso del vettore velocità v;
– modulo uguale al prodotto della massa del corpo per il modulo della sua velocità:
p = mv
– l’unità di misura di p è kg m/ s .
La quantità di moto totale ptot di un sistema composto da N corpi è la risultante delle
quantità di moto di ciascun corpo:
ptot= p1+p2+p3+…+pN=m1v1+m2v2+m3v3+……+mNvN
Supponiamo di avere due masse m1 e m2 che si muovono con velocità
v1 e v2 in assenza di forze esterne.
Il sistema è quindi isolato.
• Sia F12 la forza che la massa m2 esercita sulla massa m1 e F21 la forza
che la massa m1 esercita sulla massa m2.
• Per il principio di azione e reazione si ha:
F12= -F21
F12+F21=0
m1a1+m2a2=0
m1a1+m2a2=0
Δ v1
Δ v2
m1
 m2
0
Δt
Δt
Δ(m1 v1  m 2 v 2 )
0
Δt
(m1 v1  m 2 v 2 )  cost
Se il sistema è isolato la quantità di moto totale si conserva
In un urto:
(m1 v1  m 2 v 2 )  cost
v
m1 v  m 2 v  m1 v
in
1
v
in
1
fin
1
in
2
fin
1
 m2 v
fin
2
v
in
2
v
fin
2
Gli urti possono essere elastici o anelastici
• Urto quasi completamente elastico
Urto quasi completamente anestastico
Urto elastico in una direzione
• Oltre alla quantità di moto, si conserva anche l’energia
m v  m2 v  m v  m2 v
1
1
1
1
in 2
in 2
fin 2
fin 2
m1 (v1 )  m 2 (v 2 )  m1 (v1 )  m 2 (v 2 )
2
2
2
2
in
1 1
in
2
fin
1 1
fin
2
m1 (v  v )  m 2 (v  v )
in
1

fin
1
fin
2


in
2
m1 ( v )  ( v )  m 2 ( v )  ( v )
in 2
1
fin 2
1
fin 2
2
in 2
2


m1 (v  v )  m 2 (v  v )
in
1
fin
1


fin
2
in
2
m1 (v )  (v )  m 2 (v )  (v )
in 2
1
fin 2
1
fin 2
2
m1 (v  v ) (v  v )  m 2 (v
in
1
fin
1
in
1
fin
1
m1 (v  v )
in
1
fin
2
 v )(v
in
2

fin
2
v )
in
2
 m 2 (v  v )
fin
1
fin
2
m1 (v  v ) (v  v )  m 2 (v
in
1
in 2
2
fin
1
in
1
fin
1
(v  v )  (v
in
1
fin
1
fin
2
fin
2
v )
in
2
in
2
 v )(v
in
2
fin
2
v )
in
2
(v  v )  (v
in
1
fin
1
fin
2
v )
in
2
m1 (v  v )  m 2 (v  v )
in
1
v
fin
1
fin
1
fin
2
 v  v
in
1
fin
2
v
in
2
in
2
m 2 (v  v )  m1 (v  v )
fin
2
in
2
in
1
fin
1
m 2 (v  v )  m1 (v  (  v  v  v ))
fin
2
in
2
in
1
in
1
fin
2
in
2
m 2 (v  v )  m1 (2 v  v  v )
fin
2
in
2
in
1
fin
2
in
2
v
fin
1
 v  v
in
1
fin
2
v
in
2
m 2 (v  v )  m1 (2 v  v  v )
fin
2
(m1  m 2 ) v
v
fin
2
in
1
fin
2
in
2
 2 m v  (m1  m 2 ) v
in
1 1
in
2
2 m1
(m1  m 2 ) in
in
v 
v1 
v2
(m1  m 2 )
(m1  m 2 )
2 m1
m1  m 2 in in
in
in
  v1 
v1 
v2  v2
m1  m 2
m1  m 2
2 m2
m 2  m1 in
fin
in
v1 
v2 
v1
m1  m 2
m1  m 2
fin
2
fin
1
in
2
v
fin
1
v
fin
2
2 m2
m 2  m1 in
in

v2 
v1
m1  m 2
m1  m 2
2 m1
(m1  m 2 ) in
in

v1 
v2
(m1  m 2 )
(m1  m 2 )
Velocità finali nell’urto elastico in una direzione
Esempio 1
• Se le due masse hanno la stessa massa m=m1=m2:
dopo l’urto, si scambiano le velocità
v
fin
1
2 m2
m 2  m1 in
in

v2 
v1
m1  m 2
m1  m 2
v
fin
1
v
in
2
v
fin
2
2 m1
(m1  m 2 ) in
in

v1 
v2
(m1  m 2 )
(m1  m 2 )
v
fin
2
v
in
1
v
v
fin
1
v
in
2
in
1
v
v
fin
2
v
in
1
in
2
Esempio 2
• Se una delle due masse è molto maggiore dell’altra m1>>m2:
m1+m2≈m1
v
fin
1
m1-m2≈m1
2 m2
m 2  m1 in
in

v2 
v1
m1  m 2
m1  m 2
v
fin
1
v
in
1
dopo l’urto, m1 prosegue inalterata
2m2≈0
v
fin
2
2 m1
(m1  m 2 ) in
in

v1 
v2
(m1  m 2 )
(m1  m 2 )
v
fin
2
 2v  v
in
1
in
2
v
in
1
v
v
v
fin
2
 2v  v
in
1
in
2
fin
1
v
in
1
in
2
Esempio 3
• Se una delle due masse è molto maggiore dell’altra m1>>m2 ed è ferma :
m1+m2≈m1
v
fin
1
m1-m2≈m1
2m2≈0
2 m2
m 2  m1 in
in

v2 
v1
m1  m 2
m1  m 2
v
fin
1
0
v 0
in
1
v
fin
2
2 m1
(m1  m 2 ) in
in

v1 
v2
(m1  m 2 )
(m1  m 2 )
v
fin
2
 v
in
2
v
fin
2
 v
in
2
Se in queste condizioni, il corpo in moto ha anche una componente della velocità in
direzione y:
v
y
fin
2, x
v
x
 v
fin
2, y
v
in
2, x
in
2, y
Esercizio
• Lungo un canale veneziano, due gondole si incontrano e si fermano per scambiarsi
informazioni. La prima gondola, con a bordo solo il rematore, ha massa
complessiva di 4.7 102 kg. Terminata la chiacchierata, il primo gondoliere spinge
la gondola del collega, che ha tre passeggeri a bordo, con una velocità di 0,16 m/s,
mentre lui si allontana con una velocità di 0,21 m/s.
• Determinare la massa complessiva della seconda gondola.
m v  m2 v  m v  m2 v
in
in
v1  v 2  0
fin
fin
0  m1v1  m 2 v 2
fin
fin
m1v1   m 2 v 2
fin
v1
2 0,21
m 2   m1 fin  4.7 10
v2
0,16
2
 6.16 10 kg
in
1 1
in
2
fin
1 1
fin
2
Urto anelastico in una direzione
• La quantità di moto si conserva, l’energia cinetica no, perché viene
trasformata in altre forme di energia, suono, calore, deformazione
m v  m2 v  m v  m2 v
in
1 1
in
2
fin
1 1
fin
2
• Nell’urto completamente anelastico, le velocità finali dei due corpi
sono uguali e i corpi si muovono come un tutt’uno.
v
fin
1
v
fin
2
m v  m 2 v  (m1  m 2 ) v
in
1 1
in
2
fin
1
Esercizio 1
• L’auto del signor Bianchi, ferma al semaforo, viene tamponata da quella del signor
Rossi. Quest’ultimo, in tribunale, afferma che stava viaggiando a meno di 50
km/h. Bianchi, invece, afferma che Rossi andava molto più veloce. Dopo l’urto le
due auto sono rimaste incastrate e dalle tracce sull’asfalto si è potuto stabilire che,
immediatamente dopo l’urto, viaggiavano a 30 km/h. Il signor Bianchi guidava
una utilitaria di massa 800 kg e Rossi una berlina di massa 1400 kg. Rossi dice la
verità?
mB=800 kg
mR=1400 kg
vinB=0
vfin=30 m/s
m B v  m R v  (m B  m R ) v
in
B
in
R
m R v  (m B  m R ) v
(m B  m R ) fin
in
vR 
v
mR
(800  1400) fin
in
vB 
v
1400
2200 fin
in
vB 
v  1.57 x 30
1400
 47.1 m/s
Rossi dice la verità
in
R
fin
fin
Pressione
• La forza esercitata perpendicolarmente ad una superficie per unità di
superficie si chiama pressione
F
P
S
• Le dimensioni della pressione sono:


M xL
M
P

 2
2
2
Superficie T  L
T L
Forza
• Le unità di misura della pressione sono:
1 Pascal 
1N
1m
2
Esempi
• La pressione di un foglio di carta A4 (21x29.7 cm2)
di peso 2 g su un tavolo è:
P=mg/S=2 10-3 9.8/(0.21x0.3)=0.31 Pa
• La pressione esercitata da una bottiglia d’acqua (1,5 kg) su
un tavolo (area di appoggio pari a 5 cm2) è:
P=mg/S=1.5 x 9.8/5 10-4=3 104 Pa
• La pressione di una scure, la cui lama è lunga 10 cm e larga
0.3 mm, premuta con una forza di 300 N, su un tavolo è:
P=F/S=300 /(0.1x3 10-4 )=107 Pa
Esempi
• A parità di forza, la pressione dipende dalla superficie:
P=50kg/0.1m2=500 Pa
P=50kg/(0.3x0.1)m2=1666 Pa
P=50kg/(0.01x0.01)m2=5 105 Pa
L’aria pesa, l’esperimento di Torricelli
L’aria pesa, l’esperimento di Torricelli, cosa succede sotto vuoto:
Quanto pesa quindi l’aria?
• Quanto una colonna di mercurio di 76 cm, quindi la pressione
atmosferica è:
• 1 Atm= 760 mm Hg = 760 Torr
•
•
•
= Mg/S Pa=
= rVg/S Pa=
= 13579 x 9.8 x 0.76 Pa=
= 1.013 10 5 Pa