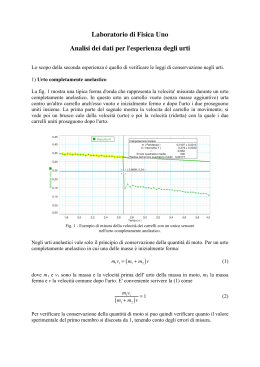
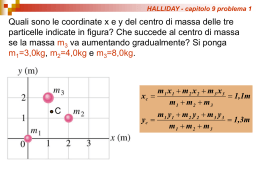
Un corpo puntiforme A di massa m in moto con velocita’ v A su di un piano orizzontale liscio
urta un corpo B identico se inizialmente il corpo B e’ fermo ai piedi di un piano inclinato liscio
nel caso entrambi i corpi siano vincolati a restare appoggiati al piano orizzontale prima ed a quello
inclinato successivamente determinare la massima quota raggiunta dal corpo B nel caso
di urto perfettamente elastico oppure di urto perfettamente inelastico
y
urto perfettamente elastico
prima dell’urto
dopo l’urto
vA  vxA iˆ e
v A'  vx' A iˆ
e
vB  0
v B'  vx' B iˆ
vA
x
nella direzione orizzontale non agiscono sul sistema forze esterne impulsive
quindi si potra’ imporre la conservazione della quantita’ di moto totale
lungo l’asse x
mentre lungo l’asse y la presenza del piano introduce un vincolo
mvxA  mvx' A  mvx' B
dato che l’urto e’ perfettamente elastico
si potra’ imporre che anche l’energia cinetica si conservi per cui
1 2 1 ' 2 1 ' 2
mvxA  mvxA  mvxB
2
2
2
vxA  vx' A  vx' B
relazioni che si riducono a
vx2A  vx' A 2  vx' B 2
e
si tratta di un sistema di due equazioni nelle due incognite
quadrando la prima delle due relazioni si ha
dovra’ aversi
o che
vx' A 2  vx' B 2  2vx' A vx' B  vx' A 2  vx' B 2
vx' A vx' B  0 affinche’ questa uguaglianza sia soddisfatta
o che entrambi i fattori siano nulli , ossia che
vx' A  0 e
vx' B
vx2A  vx' A 2  vx' B 2  2vx' A vx' B
uguagliandola alla seconda relazione si ottiene
da cui 2vx' A vx' B  0 ossia
vx' A e
vx' B  0
oppure che
vx' A  0 e vx' B  0
vx' A  0 e vx' B  0
ma l’ipotesi che entrambi i fattori siano nulli e’ in conflitto con l’ ipotesi iniziale che l’urto sia elastico
nello specifico con l’ipotesi che l’ energia cinetica sia conservata
infatti inserendo i valori v
1 2
si otterrebbe mvxA  0
2
'
xA
 0 e v  0 nella
'
xB
1 2 1 ' 2 1 ' 2
mvxA  mvxA  mvxB
2
2
2
risultato chiaramente in contraddizione le condizioni iniziali
se fosse
y
vx' A  0 e vx' B  0
significherebbe che il corpo A ha superato il corpo B
prima dell’urto
vA
e data l’impenetrabilita’ della materia cio’ sarebbe possibile
x
y
solo se il corpo A avesse scavalcato il corpo B
dopo l’urto
ma questo e’ in contraddizione con l’ipotesi iniziale che
v 'A
entrambi i corpi rimangano vincolati al piano d’appoggio
dunque l’unica soluzione accettabile e’ vx' A  0
e
x
vx' B  vxA
il che significa che il corpo A si ferma mentre il corpo B si mette in moto con la stessa velocita’
che aveva il corpo di A prima dell’urto
y
applicando al corpo B dopo l’urto la legge di conservazione
vA
dell’energia meccanica si ottiene
1 ' 2
mvxB  mgh
2
ma
vx' B  vxA
prima dell’urto
' 2
1 v xB
1 ' 2
vxB  gh da cui h 
2
2 g
2
vxA
quindi h 
2g
x
y
dopo l’urto
vA
x
urto perfettamente anelastico
come in precedenza nella direzione orizzontale non agiscono sul sistema forze esterne impulsive
quindi si potra’ imporre la conservazione della quantita’ di moto totale lungo l’asse x
mentre, dato che l’urto e’ perfettamente anelastico, non si potra’ piu’ pretendere che l’energia
ed in effetti dopo l’urto i due corpi rimangono uniti costituendo
cinetica sia conservata
un unico oggettto di massa 2m in moto con velocita’ vx' F
applicando all’urto la legge di conservazione della quantita’di moto totale
si ottiene mvxA  2mv
'
xF
da cui v
'
xF

vx A
2
applicando al corpo A+ B dopo l’urto la legge di conservazione dell’energia meccanica
1
si ottiene
2mvx' F 2  2mgh
2
2
1 vx A
quindi h 
8 g
1 ' 2
vxF  gh
2
da cui
h
' 2
v
1 xF
2 g
ma v
'
xF

vx A
2