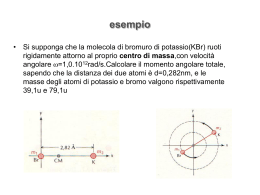
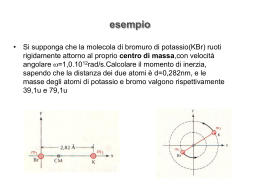
Un asticella omogenea di massa m1 e lunghezza l e’ ferma sopra un
piano liscio orizzontale. Un punto materiale di massa m2 e componente
della velocita’ perpendicolare alla sbarretta pari a v colpisce l’asta a
distanza r dal punto di mezzo O dell’asticella e vi rimane attaccato.
Determinare la velocita’ lineare ed angolare del sistema dopo l’urto
durante l’urto agiscono soltanto forze interne di conseguenza il sistema
e’ isolato e sara’ possibile imporre la conservare della quantita’ di moto
totale del sistema e del momento angolare totale
m1
mentre per quanto riguarda l’energia, dato che l’urto
e’ perfettamente anelastico, non si potra’ imporre
la conservazione dell’ energia cinetica
la velocita’ del centro di massa dopo l’urto coincidera’ con
quella del sistema asta piu’punto materiale
prima dell’urto
dopo l’urto
O
Q  m2v
l
r
Q '  (m1  m2 )vCM
m2
v
imponendo la conservazione della quantita’ di moto totale
ossia imponendo che Q’ = Q si ha
m2v  (m1  m2 )vCM
da cui
vCM
m2

v
(m1  m2 )
la velocita’ del centro di massa sara’ la stessa anche prima dell’urto
dato che non vi sono forze esterne agenti sul sistema
nell’istante in cui avviene l’urto la posizione del centro di massa
rispetto al centro dell’asta sara’
(m1  m2 ) xcm  m2 r
percio’
xcm
assumendo il centro di massa come polo si ha
m2

r
(m1  m2 )
m1
(r  xCM )m2v  I 
dove il momento d’inerzia rispetto al centro di massa
scelto come polo sara’
I  m1
l2
12
2
 m1 xCM
 m2 (r  xCM )2
si ricava quindi la velocita’ angolare
(r  xCM )m2v

m1
l2
12
2
 m1 xCM
 m2 (r  xCM )2
rm2v

l2
(m1  m2 )  m2 r 2
O
r
CM
m2
12
la rotazione avverra’ in questo caso in senso antiorario
viceversa se l’urto avvenisse con r al di sopra del centro di massa la
rotazione sarebbe oraria
dopo l’urto il centro di massa si muove con moto rettilineo uniforme
mentre gli altri punti dell’asta hanno un moto composto da una traslazione
con velocita’ pari a quella del centro di massa
e da una rotazione con velocita’ angolare  rispetto ad un asse
perpendicolare al piano e passante per il centro di massa
se r = 0 ossia se la pallina urtasse l’asticella all’altezza del centro di
massa dell’asta stessa  = 0
infine se m1 = m2 = m si ha che
1
xCM  r
2
1
vCM  v
2

rv
l
6
 r2