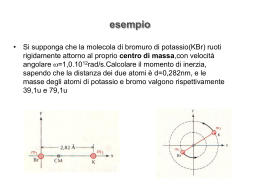
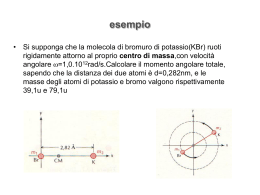
La densità come funzione di
punto
un esercizio sulla determinazione del
centro di massa di una bacchetta
sottile rigida
Calcolo del centro di massa di un corpo rigido: densità come
funzione di punto
Una sbarra sottile di lunghezza L ha una densita’ lineare
di massa  che aumenta linearmente con la distanza a
partire da un estremo. Se la massa totale della sbarretta
e’ M e la densita’ lineare dall’estremo piu leggero e’ 
trovare la distanza del CM dall’estremo piu’ leggero.
L
  0
  0  bL
problema ad una sola dimensione x
problema ad una sola dimensione x
L
0
  0
  0  bL
 ( x)  0  bx
densita’ lineare in un generico punto x
della sbarra sottile
centro di
massa
xcm
1

M
 x ( x)dx
Mxcm  0  xdx   bx dx
2
0
x
 ( x )  0  bx
Mxcm   x(0  bx)dx
Mxcm 
0
2
x
2 L
0
b 3L
 x
3 0
b 3
b 2
 0
Mxcm  L  L  L L  L 
2
3
3 
 2
L  0
b 2
dobbiamo ricavare b dai dati
xcm 
 L  L 
M 2
3 
del problema
2
ricaviamo b dai dati del problema
L
  0
  0  bL
L
L
0
0
M    ( x)dx   0  bx dx
2( M  0 L)
b
L2
Sostituendo
si trova:
massa M,
lunghezza L
densità 0 per x=0
L
1 2
1 2
M  0 x  bx  0 L  bL
2
2
0
ricordando che
L
xcm 
M
b 2
 0
 L  L 
3 
 2

M
1  2( M  0 L)  2 
xcm   0 L  
 L 
2
L
3
L
 
2
2( M  0 L) 
M
2M 0 L 
 0

xcm   L 

  0 L 

L
3
3
3 
 2

 2
da cui finalmente troviamo la coordinata
del CM in funzione dei dati del problema
2 L 0 L


3 6M
2
xCM
Eseguire i calcoli per:
M  2.5kg; L  0.6m;
0  0,05kg / m
xcm
2 L 0 L2


3 6M
Sostituiamo i valori numerici, tenendo conto che
vogliamo usare le variabili del sistema SI