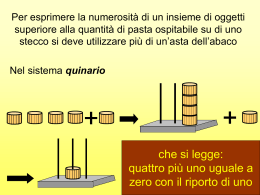
Sistemi di numerazioni e
metodi di trasformazioni
Un po’ di storia………
•
La nozione di numero, insieme a quella di grandezza risale alle
epoche più antiche in cui visse l’uomo. Come testimonianze abbiamo
le pitture rinvenute sulle pareti delle caverne preistoriche.
•
L’uomo primitivo aveva già il concetto di differenza fra una pecora e
un gregge. A poco a poco però questa osservazione delle differenze
condusse al riconoscimento delle analogie quantitative: un animale
feroce e la sua preda, una pecora con il suo agnello hanno qualcosa in
comune: il fatto di essere una coppia di elementi.
•
B.Russel, un matematico (1872-1970) scriveva in proposito:
”devono essere stati necessari molti secoli per scoprire che
una coppia di fagiani e un paio di giorni sono entrambi
espressi dal numero 2”.
Da questo si capisce che si può indicare una pecora e un gregge con un
solo numero, il numero1.
•
Il nostro sistema di numerazione si diffonde in Europa a partire dal
XIII secolo. Fino ad allora si utilizzavano i numeri romani e ci si
aiutava con degli strumenti, detti abachi, nell'esecuzione dei calcoli.
•
Il nuovo sistema giunge a noi, come vedremo, dagli arabi che a loro
volta lo avevano appreso dagli indiani. Per questo viene indicato
come sistema indo-arabico.
•
Nel mondo arabo uno dei primi riferimenti al sistema indiano si
registra verso il 650 d.C. quando un vescovo siriano, Severus Sebock,
accenna in un suo scritto ai nove segni degli Indiani con cui si riesce a
scrivere ogni numero.
•
Nel 772 il califfo Al-Mansur riceve una delegazione di astronomi e
studiosi indiani che gli portano in dono un'opera denotata dagli arabi
come Sindhind opera astronomica in cui si mostra anche come usando
solo nove segni sia possibile scrivere qualunque numero ed eseguire
facilmente calcoli. Pochi anni più tardi l'opera viene tradotta in arabo,
ma tale versione è andata perduta.
•
Negli antichi sistemi di numerazione non esisteva alcun simbolo che
rappresentava lo zero.
•
Nella lingua italiana il vocabolo zero non ha un vocabolo corrispondente, si
può trovare nihil, nullus, numerus che significano nulla, nessun numero ma
non zero.
•
Il vocabolo zero deriva dall’arabo sifr che vuol dire vuoto.Leonardo Pisano
detto “Fibonacci” nella sua opera Liber Abbaci, editata nel 1202 cercò una
parola molto simile alla parola araba e scrisse zephirus (zefiro) il termine sifr
ha dato luogo alla parola cifra, denominazione estesa a tutti i simboli del
sistema di numerazione decimale.
•
Insomma, fu con l’uso della numerazione scritta posizionale arabica, che, a
sua volta, rifletteva quella indiana, che l'Europa aveva scoperto grande
importanza dello zero.
Un sistema di numerazione è un insieme finito di simboli,detti cifre, e di
regole che consentono di rappresentare i numeri naturali.I sistemi di
numerazione possono essere suddivisi in due grandi gruppi:
1)
Sistemi additivi,in cui ogni cifra ha un valore prefissato e
immutabile mentre il valore complessivo del numero si ottiene
sommando fra loro le cifre che lo compongono;
Per esempio nella num. romana il numero 673 è rappresentato dai simboli
DCLXXIII e cioè 500+100+50+10+10+1+1+1=673.
Tale scrittura additiva dei numeri rendeva però complessa
l'esecuzione delle operazioni aritmetiche, per cui col tempo si
andò affermando il principio di posizione.
2)
Sistemi posizionali,in cui il valore di ogni cifra dipende
dalla posizione che occupa nella rappresentazione stessa.
Il sistema di numerazione più diffuso in antichità è
additivo,usato dai greci,egizi,romani e popoli d’Israele.
Sistemi di numerazioni




I moderni sistemi di numerazione sono posizionali cioè tutti i simboli
(o cifre) vengono ordinati in modo che ognuno abbia un valore di
un’unità più alto di quello della cifra precedente e quando più cifre
vengono combinate insieme il valore del numero rappresentato
dipende anche dalle loro posizioni relative.
Il numero delle cifre di cui si avvale un sistema di numerazione
prende il nome di base.
La scelta della base in un sistema di numerazione è determinata da
ragioni di comodo.

Ognuno di essi ha pregi che ne giustificano l’uso in particolari
fasi del processo di analisi digitale. Nella prima parte verranno
descritti i quattro sistemi e nella seconda si vedrà come
trasformare un numero da una forma all’altra e nella terza parte
vedremo le operazioni.
Regola generale
Regola generale:Un numero N in base b è
rappresentato da una sequenza di caratteri (cifre)
a n a n-1 ...a 2 a 1 a 0
Il valore di N è dato da:
N= a n b n +a n-1 b n-1 +...+a 2 b 2 +a 1 b 1 +a 0 b 0
con b>1 e 0<=a i <b
Rappresentazione decimale

Il sistema decimale comprende le seguenti cifre o
simboli:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
La posizione che ogni cifra ha in un numero da il peso che ha
quel numero
Esempio:
In 1.935
5 è una unità; 3 è una decina; 9 è una centinaia; 1 è una migliaia
Ogni numero ha inoltre una forma polinomiale che si scrive come
nel seguente esempio:

1.104 + 9.103 + 3.102 + 5.101

Noi, esseri umani, siamo abituati, per cultura,
ad utilizzare il sistema decimale; 10 numeri,
da 0 a 9, che identificano 10 precise
grandezze. Quando il valore da esprimere è
superiore, passiamo alla grandezza successiva
(il 10, per esempio, significa 1 decina e 0
unità; il 179 significa 1 centinaio, 7 decine e
nove unità; il 2134 significa 2 migliaia, 1
centinaio, 3 decine e 4 unità; e così via).

Sviluppando, per esempio, lo schema
matematico del numero 2134 avremo:

2
1
3
4
migliaia (1000=103) = 2000
centinaio (100=102) = 100
decine (10=101) = 30
unità (1=100) = 4

Da notare che il termine "decimale" deriva
dalla base usata (il 10, appunto) come
moltiplicatore. Ogni grandezza successiva
consiste nella base elevata alla potenza
corrispondente la posizione del valore stesso.
La posizione iniziale (unità) corrisponde alla
base (10) elevata alla potenza di 0; la
seconda posizione (decina) corrisponde alla
base (10) elevata alla potenza di 1; la terza
posizione (centinaia) corrisponde alla base
(10) elevata alla potenza di 2 … e così via.

In realtà, questo metodo di calcolo, più
complicato da spiegare che da usare, è
solo una nostra scelta per una nostra
precisa comodità (forse perché dotati
di 10 dita), ma nessuno vieta di usare
altri sistemi di calcolo basati su un
numero differente di valori.
Corrado
 È il sistema più conosciuto dall’Uomo
La base â è pari a 10
I simboli utilizzati sono 0,1,2,…,9 dal
significato ovvio
Esempio: la stringa 2349 rappresenta
il numero
2*103+3*102+4*101+9*100.
I numeri decimali sono facilmente
intelligibili


