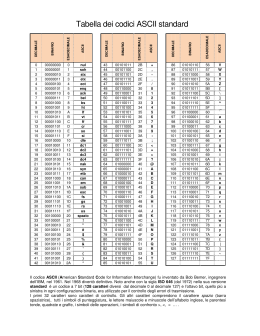
I sistemi di numerazione
decimale e binario e
la codifica delle informazioni
Che cos’è un sistema di numerazione?
E’ un insieme di regole ed oggetti per rappresentare le
grandezze numeriche
Ogni popolo del passato escogitò un proprio sistema di
numerazione parlato e scritto, nel corso della storia molti
sistemi si affermarono e poi scomparvero
I greci e i romani indicavano le cifre con lettere
dell’alfabeto, usando un sistema detto “additivo” perché il
numero è scritto come somma di simboli
Sono “posizionali” invece i sistemi in cui il valore della
cifra dipende dalla posizione che occupa all’interno del
numero stesso
Il sistema di numerazione decimale
E’ un sistema posizionale in base 10
Usa 10 simboli diversi detti cifre: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
I numeri sono rappresentati combinando le 10 cifre
Il valore del numero è dato dalla somma dei valori delle
singole cifre
Il valore di una cifra è dato dalla cifra stessa moltiplicata
per una opportuna potenza della base, legata alla sua
posizione
Esempio:
315 = 3 * 102 + 1 * 101 + 5 * 100 = 300 + 10 + 5
531 = 5 * 102 + 3 * 101 + 1 * 100 = 500 + 30 + 1
Interruttori e numeri binari
I computer operano utilizzando circuiti elettronici che
prevedono solo due possibili stati: presenza o assenza di
tensione elettrica o magnetizzazione
L’unica forma di rappresentazione degli stati assunti dai
circuiti è quella binaria:
ON → passa corrente
OFF → non passa corrente
(1)
(0)
Questo concetto può essere illustrato con un esempio,
dove sono rappresentate quattro lampadine collegate ad
una batteria elettrica mediante un interruttore:


quando l’interruttore è chiuso, la corrente elettrica fluisce
attraverso la lampadina che, di conseguenza, si illumina
quando l’interruttore è aperto, il flusso di corrente elettrica si
interrompe e la lampadina corrispondente resta spenta
0
1
0
1
Il sistema di numerazione binario
Si basa sulla notazione posizionale in base 2
Usa solo due cifre: 0 e 1
Le cifre sono anche dette bit (binary digit)
La forma polinomiale di un numero binario è la somma delle potenze di 2,
ciascuna moltiplicata per la cifra corrispondente
1 . 24
+
0 . 23
+
1 . 22
+
1 . 21
+
0 . 20
1 0 1 1 0
Cifra in
base 2
Cifra in
base 10
16
+
0
+
4
+
2
+
Risultati delle potenze di 2 moltiplicate per la cifra binaria corrispondente
0
=
22
Conversioni
Da binario a decimale: moltiplicare ogni cifra per la base
elevata alla sua posizione:
1101002 = 0 * 20 + 0 * 21 + 1 * 22+ 0 * 23 + 1 * 24 + 1 * 25 =
= 0 * 1 + 0 * 2 + 1 * 4 + 0 * 8 + 1 * 16 + 1 * 32 =
= 0 + 0 + 4 + 0 + 16 + 32 = 5210
Da decimale a binario: dividere ripetutamente il numero
per 2 fino a raggiungere lo zero. L’insieme dei resti preso
in ordine inverso rappresenta il numero binario:
52 2
0 26 2
0 13 2
1 6 2
0 3 2
11 2
1 0
5210 = 1101002
Bit e Byte
Per poter rappresentare i caratteri all’interno
dell’elaboratore le due cifre del sistema binario sono
insufficienti
Il byte è un gruppo di 8 bit e corrisponde all’unità minima
di memorizzazione per rappresentare una lettera, una
cifra o un simbolo
Il byte è l’unità di misura dell’informazione: tutte le
rappresentazioni numeriche adottate nei computers
usano un numero di bit multiplo di 8
Con 1 byte si possono ottenere 256 (28) combinazioni di
0e1
Mediante una tabella di codifica ogni byte viene
associato a una specifica lettera, a un determinato
numero, a un simbolo
Il codice ASCII
(American Standard Code for Information Interchange)
Il codice ASCII è stato elaborato per assegnare in modo
univoco una cifra binaria ad ognuno dei caratteri
alfanumerici utilizzati nella comunicazione scritta
Ogni simbolo viene memorizzato in un byte: per questo
motivo il codice ASCII esteso può rappresentare 256
simboli diversi
Un messaggio scritto sarà quindi formato da tanti byte
quanti sono i caratteri utilizzati
A differenza dei valori numerici, la corrispondenza tra un
dato carattere o simbolo e la combinazione di 1 e 0
presenti nel byte che li rappresenta è puramente
arbitraria
Il codice ASCII copre solo i primi 128 (27) caratteri,
numeri e simboli
La tabella ASCII estesa è costituita da 256 (28) elementi
e presenta varie versioni a carattere nazionale
In questa tabella sono rappresentati otto simboli e il numero binario che li
rappresenta nel codice ASCII
RAPPRESENTAZIONE BINARIA
NUMERO
DECIMALE
CODICE
ASCII
RAPPRESENTAZIONE BINARIA
NUMERO
DECIMALE
CODICE
ASCII
00101011
43
+
01100001
97
a
00101101
45
-
01000001
65
A
00101010
42
*
01100010
98
b
00101111
47
/
01000010
66
B
Con un byte possiamo
rappresentare 256 valori
(da 0 a 255)
Il codice ASCII assegna
ad ognuno di questi
valori un diverso simbolo
Il codice UNICODE
E’ stato sviluppato grazie all’introduzione di memorie
sempre più capaci
Mette a disposizione 65.536 (216) caratteri
E’ possibile codificare le lettere e le cifre delle principali
lingue del mondo, anche quelle che usano ideogrammi
come cinese e giapponese