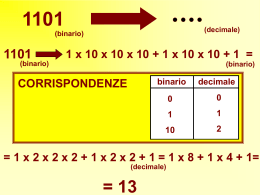
Sistemi di numerazione
Sistema di numerazione decimale
Sapete già che il problema fondamentale della numerazione consiste nel rappresentare con un
limitato numero di segni particolari, detti cifre, tutti gli infiniti numeri naturali. Per stabilire un
sistema di numerazione occorre fissare una base che è del tutto arbitraria e, rappresentati con delle
cifre i numeri minori della base, individuare tutti i numeri maggiori di essa con un allineamento di
quelle cifre.
Nel sistema decimale, o a base dieci, i numeri minori della base si rappresentano con le cifre:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
e si dicono unità del primo ordine. Si conviene poi che dieci unità del primo ordine formano una
decina, o unità del secondo ordine, che dieci unità del secondo ordine formano un centinaio, o
unità del terzo ordine, e così via. Cioè dieci unità di un dato ordine formano un'unità dell'ordine
immediatamente superiore.
Le unità dei successivi ordini, in tale sistema di numerazione, sono rappresentate da:
1 =10° , 10=101, 100=102, 1000=10 3 , ecc
Un qualsiasi numero intero si rappresenta con un allineamento di alcune delle cifre, con la
convenzione che:
Qualunque cifra posta a sinistra di un'altra rappresenta unità dell'ordine immediatamente
superiore a quello rappresentato da quest'ultima.
Perciò, per scrivere un numero enunciato si dispongono da sinistra verso destra le cifre che
indicano quante sono le unità dei vari ordini cominciando dal più alto, e se nel numero considerato non vi sono unità di un certo ordine, si pone uno zero al posto che doveva essere
occupato da quelle unità.
Così ad es. il numero duecentocinquantotto è formato da otto unità del primo ordine, da cinque
unità del secondo ordine (o cinque decine), e da due unità del terzo ordine (o centinaia), e si
rappresenta per la convenzione fatta, con la scrittura: 258.
Considerate un qualsiasi numero intero, ad es. quello che nella numerazione decimale si indica
con la scrittura: 3.542;
poiché le cifre 2, 4, 5, 3, rappresentano rispettivamente le unità semplici, le decine, le centinaia e
le migliaia del numero considerato, esso può anche scriversi sotto questa forma che è detta
polinomiale:
3542 = 3 x 1000 + 5 x 100 + 4 x 10 + 2
e poiché:
1000 = 103,
100 = 102,
10 = 101,
Il dato numero può anche scriversi nel modo seguente:
3542 = 3x103 + 5x102 + 4x101 + 2x100.
1 = 100
Dunque:
Qualunque numero intero, maggiore di nove, si può sempre rappresentare come somma di
prodotti di numeri minori della base 10, per potenze decrescenti della base stessa.
Finora abbiamo considerato come base del sistema di numerazione il numero 10, ma si riconosce
facilmente che tutto quanto si è premesso vale qualunque sia la base che si sceglie per il sistema di
numerazione.
Stabiliamo ad es. che:
Fissata una qualsiasi base, ad es. 5, ogni numero intero maggiore di 5, si può sempre
rappresentare come somma dei prodotti di numeri interi minori di 5 per potenze decrescenti
di tale base.
Proponiamoci ad es. di rappresentare nel sistema di numerazione a base 5 il numero che nel sistema
decimale è rappresentato dalla scrittura: 298.
In questo sistema bastano le sole cinque cifre: 0, 1, 2, 3. 4, per rappresentare un numero intero
qualsiasi.
Per raggiungere tale scopo, dividiamo il dato numero 298 per la base 5 ed avremo:
Praticamente l'operazione si dispone nel modo seguente:
298
5
48
3
59
9
4
5
11
1
5
2
Si divide 298 per la base 5 e si ha per quoziente 59 e per resto 3; si divide 59 per 5 e si ha come nuovo quoziente 11 e per
resto 4. Il quoziente 11 si divide ancora per 5 e si ha come quoziente 2 e per resto 1 Poiché quest'ultimo quoziente 2 è
minore della base 5, l'operazione è terminata, ed i successivi resti trovati a partire dal primo, e l'ultimo quoziente,
cioè le cifre 3, 4, 1, 2, rappresentano rispettivamente le unità del primo, secondo, terzo ordine, ecc. del numero
considerato espresso nella base 5, quindi:
298(10) = 2143(s)
Proponiamoci ora di stabilire qual è il numero che nella numerazione decimale equivale ad un dato numero scritto
in un sistema di diversa base.
Stabiliamo ad es. qual è il numero che nella numerazione decimale equivale a quello che nel sistema a base 5 è
indicato con la scrittura: 3214(5).
Esso è formato da 4 unità semplici, da 1 unità del secondo ordine, da 2 unità del terzo ordine e da 3 unità del quarto
ordine, e poiché nel sistema a base 5 ogni unità di un dato ordine è uguale a 5 unità dell'ordine immediatamente
inferiore, il dato numero è formato dal seguente numero di unità semplici:
3 2 1 4 = 3 x 5 3+2x52+1x51+4x50 = 375+50+5+4 = 434
dunque:
3214(5) = 434(10)
NUMERAZIONE BINARIA
Un sistema di numerazione particolarmente notevole è quello a base 2, detto anche sistema
binario. In tal caso invece delle dieci cifre del sistema decimale, bastano le due sole cifre: 0 ed 1
per poter rappresentare qualsiasi numero intero. In tale sistema un'unità del secondo ordine vale 2
unità semplici, una unità del terzo ordine vale 2 unità del secondo ordine, ossia 4 unità semplici,
un'unità del quarto ordine vale 2 unità del terzo ordine, ossia 8 unità semplici, e così via.
Quindi nel sistema di numerazione binaria, le unità del primo, secondo, terzo, quarto, ecc., ordine
equivalgono rispettivamente al seguente numero di unità semplici:
1, 2, 4, 8, 16, 32,
che possono anche scriversi sotto la forma: 2 0,
21,
22,
23,
ecc
Analogamente a quanto si è visto per la numerazione decimale, qualunque numero intero
maggiore di uno si può sempre rappresentare come somma di prodotti di numeri minori della base
2, per potenze decrescenti di tale base.
Così ad es. nella numerazione binaria, la scrittura: 1101(2)
indicando il numero formato da un'unità del primo ordine, da zero unità del secondo ordine, da
un'unità del terzo e da una del quarto ordine, può anche scriversi sotto la forma:
1101 (2) = 1 x 2 3 + 1 x 2 + 0 x 21 + 1 x 20
e viceversa, l'espressione: 1 x 23 + 1 x 22 + 0 x 21+ 1 x 20 equivale nel sistema binario al numero:
1101(2).
Proponiamoci di esprimere nel sistema di numerazione a base 2, un qualsiasi numero intero,
ad es. quello che nella numerazione decimale si indica con la scrittura 23.
Procedendo in modo analogo a quanto si è fatto in precedenza basterà eseguire le seguenti
divisioni successive del numero dato per 2:
23
1
2
11
1
2
5
1
2
2
0
2
1
I resti che man mano si ottengono e l'ultimo quoziente (cioè: 1, 1, 1, 0, 1) rappresentano le unità
del primo, secondo, terzo ordine, ecc., quindi per le convenzioni fatte il numero dato può scriversi
sotto la forma:
23(10) =1 x 24 + 0 x 23 + 1 x 22 + 1 x 21 + 1 x 20
Ossia 23(10) = 10111(2)
Similmente volendo trasformare nel sistema binario il numero che nella numerazione decimale si indica
con la scrittura 42, si ha:
42
0
2
21
1
2
10
0
2
5
1
2
2
0
2
1
quindi: 42(10) = 1 x 2 5 + 0 x 24+ 1 x 23 + 0 x 2 2 + 1 x 2 1 + 0 x 20
42(10) = 101010(2).
Perciò
Il numero che nel sistema binario è indicato con la scrittura: 101101(2) è formato dal seguente numero
di unità semplici:
101101(2) = 1 x 2 5 + 0 x 24 + 1 x 2 3+ 1 x 22 + 0 x 2 ' + 1 x 2 0 = 32+8 +4+ 1 = 45
quindi: 101101(2) = 45(10)
Rappresentiamo il numero 173 sia nel sistema decimale, sia in quello binario. Si ha:
173
1
2
86
0
2
43
1
2
21
1
2
10
0
2
5
1
2
2
0
2
1
Quindi 173(10) = 10101101(2)
Come potete osservare il sistema di numerazione binario richiede un minor numero di simboli per
esprimere un qualsiasi numero intero, ha però l'inconveniente di dar luogo ad espressioni alquanto
lunghe per rappresentare numeri non eccessivamente grandi.
OPERAZIONI FONDAMENTALI ESEGUITE CON NUMERI ESPRESSI NEL SISTEMA
BINARIO
Le regole che avete appreso per eseguire le operazioni fondamentali dell'aritmetica sono indipendenti
dalla base che si sceglie per il sistema di numerazione.
Diamo alcuni esempi di operazioni eseguite nel sistema binario.
ADDIZIONE
Si procede con le regole a voi già note, facendo però attenzione di riportare un'unità dell'ordine
superiore ogni volta che se ne hanno due dell'ordine inferiore.
Proponiamoci di eseguire nel sistema binario l'addizione che nel sistema decimale è indicata con la
scrittura:
54 + 36 = 90.
Si ha:
54(10) = 110110(2) e 36(10) = 100 100(2)
quindi eseguendo si ha:
1 1
110110+
100100 =
1011010
La somma delle unità semplici è zero, perciò si scrive 0 nella colonna delle unità semplici; la somma delle
unità di secondo ordine è 1+0 = 1, che si scrive nella colonna delle unità di secondo ordine, la somma
delle unità del terzo ordine è 1+1, si hanno cioè due unità del terzo ordine che valgono un'unità del
quarto ordine, quindi si scrive 0 nella colonna delle unità del terzo ordine e si riporta un'unità in
quella del quarto ordine, e così via.
Si è trovato che:
110110(2) + 100100(2) = 1011010(2)
e se trasformiamo la somma ottenuta nel sistema decimale avremo:
1011010(2) =1 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 = 64+16+8+2=90
SOTTRAZIONE
Si procede con la nota regola: se accade di dover sottrarre dalla cifra 0 la cifra 1, occorre prendere
in prestito un'unità alla cifra che rappresenta unità dell'ordine immediatamente superiore, cioè di
quella che nel minuendo è situata a sinistra ditale 0, e tenere conto che tale unità ricevuta in prestito vale 2
unità dell'ordine immediatamente inferiore.
Proponiamoci ad es. di eseguire nel sistema di numerazione binario, la sottrazione che nel sistema
decimale è indicata con la scrittura:
21 - 10 = 11.
Si ha:
21(10)= 10101(2)
e 10(10) = 1010(2)
quindi:
2
2
10101 1010 =
1011
perciò: 10101(2) - 1010(2) = 1011(2)
Se trasformiamo la differenza trovata, nel sistema decimale avremo:
1011(2) =1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 = 8+2+1 = 11
MOLTIPLICAZIONE
Occorre tenere presente che nei riporti, ogni due unità di un certo ordine equivalgono ad un'unità
dell'ordine immediatamente superiore.
Diamo un esempio di una moltiplicazione eseguita prima nei sistema decimale e poi in quello
binario.
Si voglia ad es. eseguire il prodotto: 5 x 6 = 30;
I due fattori 5 e 6 nel sistema binario si indicano con le scritture:
5(10) = 101(2) e
6(10) = 110(2)
perciò eseguendo la moltiplicazione di tali numeri, si ha:
101 x
110 =
000
101101 - 11110
Il prodotto è perciò il numero: 11110(2) che nel sistema decimale equivale a:
11110(2) =1 x 2 4 + 1 x 23 + 1 x 22 + 1 x 21 + 0 x 20 = 16+8+4+2 = 30.
DIVISIONE
Anche la divisione si esegue con un procedimento perfettamente analogo a quello del sistema decimale:
basta tenere conto della regola con la quale si effettua la sottrazione e della relazione che intercorre
fra i vari ordini.
Diamo l'esempio di una divisione eseguita prima nel sistema decimale e poi in quello binario.
Si ha ad es.:
58 : 5 = 11 con resto 3
e poiché il dividendo ed il divisore nel sistema binario sono rappresentati dai simboli:
58(10) = 111010(2)
e
5(10) =101(2)
si ha:
111010
101
100
000
1001
101
1000
101
11
101
1011
quindi: 111010(2) : 101(2) = 1011(2) con resto 11(2)
Il quoto è 1011(2) ed il resto è 11(2) che nel sistema decimale equivalgono rispettivamente a:
1011(2) =1 x 23 + 0 x 22 + 1 x 21+ 1 x 20 = 8+2+1 = 11 ed il resto è: 11 (2) = 1 x 21 + 1 x 20 = 3
L'aritmetica binaria e i calcolatori
Sul sistema binario si può fare un'osservazione: se è vero che si usano solo i simboli 0 e 1 e che le
operazioni sono semplicissime è altrettanto vero che numeri naturali relativamente piccoli richiedono
molte cifre per la loro scrittura.
Ad esempio: 86(10) = 1010110(2)
È per questo motivo che viene preferito il sistema a base dieci.
Tuttavia, il fatto che nel sistema binario i simboli necessari
siano solo due, cioè 0 e 1, trova un'importantissima applicazione
nei calcolatori elettronici.
I simboli 0 e 1 corrispondono alle due situazioni in cui si può
trovare un circuito elettrico (figura 1): circuito aperto (non passa
corrente: 0) e circuito chiuso (passa corrente: 1).
Combinando insieme più circuiti, si può ottenere
un sistema di lampade, ciascuna delle quali corrisponde a un
determinato ordine del sistema binario (figura 2): lampada accesa 1,
lampada spenta 0.
Per quanto possa sembrare incredibile, tutti i calcolatori, anche quelli in grado di stabilire l'orbita di un veicolo
spaziale, sono fondati su queste semplici considerazioni. Il calcolatore elettronico resta però una macchina
estremamente complessa, per l'enorme numero di. circuiti più o meno complicati di cui si compone. Ma quello
che è veramente impressionante è l'enorme velocità con cui un calcolatore esegue le operazioni: calcoli che
richiederebbero tempi lunghissimi se eseguiti dall'uomo, sono effettuati quasi istantaneamente dal calcolatore.
Ciò è potuto avvenire grazie agli straordinari progressi della microelettronica, che ha consentito di costruire
calcolatori sempre più piccoli, sempre più potenti, sempre più veloci.
Numero binario = 010011(2)
Numero decimale corrispondente:
0 x 2 5 + 1 x 24 + 0 x 23 + 0 x 22 + 1 x 21 + 1 x 20=
16+2+1 = 19