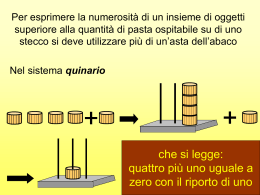
Sistemi di numerazione
e tecniche di calcolo
nell’antichità
Livia Giacardi
Liceo Classico Alfieri – Marzo 2006
Il contare fu con ogni probabilità uno dei primi processi
“matematici” che l'uomo sviluppò.
Alle origini del contare pare ci sia stata la capacità di distinguere
uno da molti che poi si evolve nel distinguere uno, due, molti
(traccia di questo passaggio rimane nel duale usato accanto al
singolare e al plurale in varie lingue antiche).
Gli studi antropologici sulle tribù primitive attuali confermano
questa ipotesi:
Indigeni della Tasmania: mara = 1, pue = 2, lô-we = un
poco, kate = molto
Tribù dello stretto di Torres: urapun =1, okosa = 2, okosaurapun = 3, okosa-okosa = 4, … ras = molti
Kamilaroi (Australia), Botocudos (Terra del Fuoco), Pigmei
(Africa), ...
1
Uno dei primi e fondamentali insiemi a cui gli uomini fecero
riferimento fu quello delle dita di una mano con cui si contava
fino a cinque, poi di due mani con cui si arrivava fino a dieci, e in
alcuni casi anche quello delle dita dei piedi per raggiungere il
venti.
Calcolo digitale in Egitto, 2600 a. C
Leonardo Pisano, Liber Abaci, 1202
Più avanti, per conservare
l'informazione, si usarono tacche su
ossa o segni su pietre. Uno dei più
antichi reperti che ci sono rimasti è
costituito da un osso con
cinquantacinque tacche, trovato nel
1937 a Dolni Vestonice
(Cecoslovacchia centrale), che risale a
30.000 anni fa.
35.000-20.000 a.C
Le cinquantacinque tacche sono disposte a gruppi di cinque.
La venticinquesima tacca è lunga il doppio delle altre.
In questo reperto sembrano dunque essere presenti i due
concetti fondamentali:
♦ la corrispondenza biunivoca tra la rappresentazione usata
(insieme delle tacche) e l'insieme di oggetti da contare
♦ e il concetto di base per un sistema di numerazione.
2
La necessità di superare le difficoltà insite in una pratica numerica
basata sulla corrispondenza biunivoca fra tacca e oggetto
condusse gli uomini all’uso di una scala di simboli
il 1° dei quali rappresenti un solo oggetto (unità semplice),
il 2° rappresenti un determinato numero b (per es. 10) di unità
semplici (unità del 1° ordine), il 3° rappresenti b unità del 1°
ordine (per es. 10×10=100), ecc.
b si dice base del sistema di numerazione
Le basi più usate fin dall’antichità sono la base 5 e la base 10
collegate con l’abitudine di contare con le mani, ma furono
utilizzate anche altre basi, quali per esempio la base 20, la base
60, la base 2.
Sistemi di numerazione additivi
Sistemi di numerazione posizionali
Sistema di numerazione additivo (e varianti)
i numeri sono scritti giustapponendo simboli
e di questi simboli si somma il valore
Il sistema di numerazione romano è additivo-sottrattivo
I
V
X
L
C
D
M
1
5
10
50
100
500
1000
XXXVII → 10+10+5+1+1= 37
IX → 10-1= 9
Es.
Sistema di numerazione posizionale
Il valore del simbolo dipende dalla posizione che occupa
Il nostro sistema di numerazione è decimale posizionale
0 1
2 3
4 5
6 7
8 9
Es. 1111 = 1×1000 + 1×100 + 1×10 + 1
= 1×103 + 1×102 + 1×10 + 1×100
scrittura polinomiale
del numero
3
Esercizio
Quale fra le seguenti scritture polinomiali è uguale a
12×102 + 103×10 + 14?
1) 2×104 + 2×103 + 4×102 + 4×101 + 0×100
2) 1×103 + 1×102 + 6×101 + 4×100
3) 2×103 + 2×102 + 4×101 + 4×100
(10+2)×102 + (102 +3)×10 + 10 + 4
103 + 2×102 + 103 +3 ×10 + 10 + 4
2×103 + 2×102 + 4×101 + 4×100
Domanda
Che effetto produce nel nostro sistema di numerazione
mettere uno zero in posizione finale?
I quipu degli Incas (XV sec.)
Il quipu = nodo consisteva in una cordicella
a cui erano annodate altre cordicelle
multicolori legate a intervalli regolari da
differenti tipi di nodi.
Sistema di numerazione decimale
posizionale.
Erano utilizzati per inventari, archivi,
censimenti.
4
Gli esagrammi di Fu-hi e la base 2
I Ching o Libro delle variazioni (300 a.C.)
Dalla combinazione dei due segni
possiamo formare 8
trigrammi (cova) e disponendo due trigrammi uno sull’altro si
costruiscono 64 esagrammi. Questi esagrammi furono messi poi in
relazione con la teoria delle due forze Yin (l’oscurità, la femminilità), e
Yang (la luce, la mascolinità), i due principi posti all’origine
dell’universo.
Il filosofo e matematico G. W. Leibniz
interpretò (1703) gli esagrammi di Fuhi come la scrittura dei primi 64 numeri
naturali in forma binaria e indagò
le “mirabili proprietà della diadica”
0
1
5=1×22+0×21+1×20
1
0
1
Scrivi in notazione binaria i seguenti esagrammi di
Fu-hi e converti in base 10
1×25 + 0×24 + 1×23 + 1×22 + 0×21 + 1×20
1
0
1
1
0
1
32 + 8 + 4 +1 = 45
1×25 + 1×24 + 1×23 + 1×22 + 1×21 + 1×20
1
1
1
1
1
1
32 + 16 + 8 + 4 + 2 + 1 = 63
45
44
1
2
22 2
22 11 2
0 10 5 2
1 4 2
1 2
0
1011012
2
1
22
22
0
2
11 2
10 5 2
1 4 2 2
1 2 1
0
101102
5
Perché si procede così?
“Scriviamo” 22 in base 2 usando l’abaco
1
passo
2
passo
3
passo
Perché si procede così?
“Scriviamo” 22 in base 2 usando l’abaco
4
passo
5
passo
1
0
1
1
0
6
Esercizi di aritmetica binaria
1011+
110
1011 110
10001
Ricordare che
1+1 = 10
101
1011 ×
110
0000
1011
1011
1000010
La moltiplicazione binaria è
molto semplice perché gli unici
numeri per cui si moltiplica
sono 0 e 1
I Maya e la base 20
I Maya, uno dei popoli più evoluti dell’America precolombiana
(III-X sec.), usavano un sistema di numerazione in base 20.
La notazione era posizionale:
utilizzavano un puntino • per l’unità,
una barretta orizzontale
per le
cinquine, e il simbolo
per lo zero.
Un sistema di numerazione in base
20 procede secondo le
successive potenze di 20
1, 20, 202, 203, 204, …
7
Invece di procedere per potenze successive di 20,
si procedeva così:
1, 20, 18×20, 18 ×202, 18 ×203, …
Questo fa sì che lo zero maya non poteva avere il
ruolo di operatore.
In una numerazione in base 20 senza anomalie,
l’aggiunta di uno zero finale moltiplica il numero per
20, cioè ha funzione di operatore:
Es. 1220
12020
1×20 + 2 = 22
1×202 + 2×20 + 0 = 440
Nella numerazione Maya
1×20 + 2 = 22
1220M
12020M
1× (18×20) + 2×20 + 0 = 400
8
L’anno per i Maya consisteva di 18 mesi di 20 giorni
ciascuno, più 5 giorni “vuoti” considerati infausti.
Codice di Dresda, XII sec.
Pagina 24 del Codice di Dresda
9
Bibliografia essenziale
Buffa G., 1986, Fra numeri e dita, Bologna Zanichelli
Boyer C., 1980, Storia della matematica, Mondadori, Milano, Cap. 1
Ifrah G., 1984, Storia universale dei numeri, Mondadori, Milano
Sistema di numerazione
e tecniche di calcolo
nell’antico Egitto
10
Inno al Nilo
“Salute a te o Nilo che sei uscito dalla terra
che sei venuto a far vivere l’Egitto!
Occulto di natura, oscuro di giorno,
lodato dai suoi seguaci;
È lui che irriga i campi, che è creato da RA per
far vivere tutto il bestiame …”
Fonti per la matematica
egizia
I testi matematici egizi di epoca pre-greca finora conosciuti sono
sette e appartengono all'arco di tempo che va dal 2000 al 1600 a.C.
e sono scritti in ieratico, la scrittura corsiva egizia:
Papiro Rhind (circa 1650 a.C.), Eisenlohr 1877, Peet 1923, A. Chace 1927
Rotolo di Cuoio ( circa 1650 a.C.), Glanville 1927
Papiro di Mosca ( circa 1850 a.C.), Struve 1930
Papiro di Berlino ( circa 1800 a.C.), Schack-Schackenburg 1900
Papiro di Kahun ( circa 1850 a.C.), Griffith 1898
Papiro Reisner ( circa 1880 a.C.), Simpson 1963-69
e due tavolette di legno risalenti al 2000 a. C., 1901, 1906
Lo studio di questi testi ebbe inizio oltre un secolo fa dopo che fu
decifrata, ad opera di J.F. Champollion (1790-1832), la scrittura
egizia.
11
La stele di Rosetta fu scoperta nel 1799 da un
ufficiale del Genio francese P. F. Bouchard;
presentava inciso un decreto di Tolomeo V
scritto in geroglifico, demotico e greco.
La stele di Rosetta
L’inglese T. Young si cimentò nella
decifrazione senza ottenere risultati definitivi.
Ci riuscirà Champollion che, fin dall’età di 14
anni, aveva cominciato a interessarsi di
geroglifici e aveva studiato in poco tempo oltre
al latino e al greco anche l’ebraico, il siriaco,
il caldeo e il copto.
486 parole greche per
1419 geroglifici
“Mi dedico interamente al copto… Voglio
conoscere l’egiziano come il mio francese
… traduco in copto tutto ciò che mi passa per la
testa, parlo copto da solo… Dopo di ciò mi
dedicherò ai papiri” (1807)
Lo storico greco Erodoto (V sec. a.C.) fa risalire l'origine della
geometria agli Egizi. La molla che li spinse a sviluppare certe
conoscenze geometriche fu la necessità di misurare i campi dopo
le periodiche inondazioni del Nilo.
Rimangono molte testimonianze di viaggi in Egitto e in
Mesopotamia da parte dei matematici e filosofi greci
(Talete, Pitagora, Democrito, Platone, Eudosso, …)
per imparare la geometria
12
Cappella dello scriba Maia, Torino nel Museo Egizio, 1400 a. C.
A. Speiser (1956) ha
dimostrato che negli
ornamenti delle tombe egizie si
trovano tutti i 17 tipi possibili
di tassellazione del piano
13
Caratteri della matematica egizia
♦ I problemi sono generalmente pratici, connessi con l'ingegneria
edile, con la distribuzione di vettovaglie tra soldati e operai,
con l'attività agricola o sono problemi di tipo amministrativo relativi a
contratti, elargizioni, corresponsione di paghe, censimenti, tassazione
e bilanci.
♦ le soluzioni sono ricette di calcolo
non c’è simbolismo, non ci sono formule
non ci sono spiegazioni dei procedimenti, né dimostrazioni
♦ non c’è suddivisione fra aritmetica, algebra, geometria
♦ livello prescientifico
♦ manuali scolastici
Casa dei rotoli di papiro
biblioteche, archivi
insegnamento di livello elementare
scrivere e contare
Case della vita
insegnamento superiore
specializzazione
Lettera dello scriba Hori ad Amenemope
“Deve essere costruita una rampa di 730 cubiti, larga 55,
consistente di 120 corsi di mattoni, alta 60 cubiti alla sommità, 30
alla metà, mentre l'inclinazione è di 15 cubiti. Viene richiesta la
quantità di mattoni necessari per essa”.
“Devi vuotare il magazzino che è pieno di sabbia fatto sotto
l'obelisco: misura 30 per 20 cubiti in pianta e conta 100 scomparti
larghi 44 e alti 50 cubiti. Calcola quanti uomini possono vuotarlo
in 6 ore”.
“Ti trovi in Siria con un corpo di spedizione di 5000 uomini. Ti
sono portate provvigioni inferiori al fabbisogno regolare di razioni
giornaliere di pane, carne e birra. Ripartiscile in proporzione a
quanto è dovuto ad ognuno”.
14
Sistema di numerazione e tecniche di
calcolo nell’aritmetica egizia
Papiro Rhind (1800, 1650 a.C.)
“Regole per scrutare la natura e per conoscere tutto ciò che esiste,
ogni mistero, ogni segreto … Fu lo scriba Ahmose a scrivere questa
copia”
Sistema di numerazione decimale additivo
senza lo zero
1
10
100
1000 10.000
100.000 1.000.000
406
6705
5.080.030
15
I numeri nei bassorilievi
11.110
2500 a. C.
121.200
46
Il passaggio dalla scrittura geroglifica a quella ieratica
(circa 2400 a.C.) portò spesso a raggruppare in un unico
segno i simboli ripetuti producendo così un aumento del
numero dei simboli numerici.
16
1/n
< r > = parte
n
Cubito reale, circa 1550 a.C.
1
2
2
3
frazione unitaria generica
(Rhind 38 e 61)
< rwy >= le due parti
< ty.t > = segno, figura
19 = 2 + 1 + 1 (Rhind 24)
8
4 8
L'insieme numerico su cui operano gli Egizi è l'insieme dei numeri
naturali escluso lo zero cui vanno aggiunte tutte le frazioni del
tipo 1/n con n intero positivo e la frazione particolare 2/3.
Come eseguire le addizioni
162 + 43
205
17
La moltiplicazione e la divisione
Il metodo di calcolo è basato su raddoppiamenti successivi
e si fonda sul fatto che ogni numero naturale diverso da 0 si può
esprimere in uno ed un solo modo come somma di potenze distinte
di 2 con esponente intero ≥ 0.
(Rhind, 32)
12×12= 22×12 + 23×12 = 48 + 96 = 144
Esercizi
24×37 =
23×12 =
1
37
2
4
8
74
148
296
16
592
24
888
1
10
2
23
230
46
12
276
18
“ouah-tep em 80 er gemet 1120”
“opera a cominciare da 80 fino a ottenere 1120”
Per dividere 1120 per 80 occorre dunque cercare per quale
numero occorre moltiplicare 80 per ottenere 1120
Esercizio
825 : 33 =
1
2
4
8
16
33
66
132
264
528
25
825
825 = 33×1 + 33×8 + 33×16
= 33×20 + 33 ×23 +33×24
19
Non sempre nella divisione si può ottenere il
dividendo come somma di multipli del divisore, per
cui si ricorre ai sottomultipli
si incomincia a dividere per 2 dal momento in cui la
somma dei dividendi parziali supera 19
La successione dei moltiplicatori non è fissa e l’abilità
dello scriba sta nel trovare la successione migliore
16 : 3 = 1 +4 + 1/3
(Rhind, 25)
1
2
4
2/3
1/3
1+4+1/3
3
6
12
2
1
20
Tavola 2: n (Rhind recto)
con dispari da n=5 a n=101
Tavola
(Rhind 61 e 61b)
“Per calcolare: 2/3 di una frazione unitaria (ty.t gbt). Se
ti viene chiesto quanto vale due terzi di 1/5 tu devi
raddoppiarlo [il denominatore] e prendere sei volte di esso
[del denominatore] cioè : 2/3 di 1/5. Si procede allo stesso
modo per qualunque frazione unitaria”
2 1= 1 + 1
3 n 2n
6n
21
Il Metodo degli ausiliari rossi (Rhind,
Rhind, 37)
Aggiungi:
1
2
+ 14 + 18 +
1
72
8
+ 161 +
36
1
32
18
+
1
64
9
+
Totale
1
576
1
1
8
72
In sostanza lo scriba riduce allo stesso denominatore le ultime
cinque frazioni:
1
2
+ 14 + 18 +
8
576
+
36
576
+
18
576
+
9
576
+
1
576
= 12 + 14 + 18 +
72
576
= 12 + 14 + 18 + 18 = 1
Quelli che per noi sono i numeratori delle cinque frazioni ridotte a
denominatore comune 576 sono scritti in rosso, ciascuno sotto la
frazione corrispondente; la loro somma 72 è 1 di 576. 1 sommato
8
8
alle tre frazioni rimanenti dà l’unità.
Il metodo degli ausiliari rossi consente di ovviare
all’assenza del concetto generale di frazione.
L’occhio di Horus
“Questo è l’occhio di Horus
Afferralo in modo che tu sia
vittorioso”
(Testi delle Piramidi)
22
<udjat> = intero
alle sei parti dell’occhio di Horus corrispondono
frazioni di hekat unità di misura per i cereali
1/2+1/4+1/8+1/16+1/32 + 1/64 = 63/64
Bibliografia essenziale
AAVV, 1987, L’alba dei numeri, Bari, Dedalo
AAVV, 1997, La scuola nell’antivo Egitto, Torino, Museo Egizio
Buffa G., 1986, Fra numeri e dita, Bologna, Zanichelli
Curto S., L’antico Egitto, Torino, UTET
Giacardi L., S. Roero, La matematica delle civiltà arcaiche (Egitto,
Mesopotamia, Grecia), Stampatori, Torino, 1979, Cap. 2
Giacardi L., La matematica dell'antico Egitto, Atti del Convegno
Il pensiero matematico nella ricerca storica italiana
Ancona 26-28 marzo 1992, Quaderni di "Innovazione
Scuola" 13, Ancona, 1993, pp. 21-49
Boyer C., 1980, Storia della matematica, Mondadori, Milano, Cap. 2
Kline M., 1991, Storia del pensiero matematico, Torino, Einaudi, Cap. 2
I testi
Chace A. e altri The Rhind Mathematical Papyrus, 2 voll.,
Oberlin Ohio, 1927-29
23