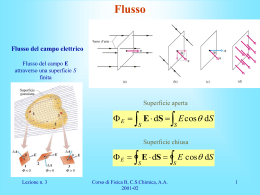
ELETTROOSTATICA
IN “APPROCCIO GLOBALE”
• Legge di Gauss;
• Esercizi e applicazioni (campo di una sfera
uniformemente carica, campo di una
distribuzione piana di carica, campo generato
da due piani paralleli carichi, campo di una
distribuzione cilindrica);
• Il flusso del vettore campo elettrico
 RIASSUNTO DELLE
PUNTATE PRECEDENTI
•
•
•
•
Elettrostatica: approccio locale
Magnetostatica: approccio locale
Conduzione elettrica stazionaria
Magnetostatica e conduzione elettrica
 QUESTA SETTIMANA
•Elettrostatica: approccio “globale” (Gauss)
•Elettrostatica nella materia
•Energia elettrostatica in approccio “globale”:
energia del campo
•Magnetostatica: approccio globale (Ampère)
Flusso del campo elettrico attraverso una superficie
i  Ei Ai cos i
se Ai  0
 
d  E  un dA

un è il versore perpendico lare a dA
Sommando su tutta una superficie chiusa:
 
   E  un d A
Derivazione della Legge di Gauss
CASO 1)
Consideriamo una carica q all’interno
di una superficie chiusa S. Il flusso totale
del campo elettrico prodotto da q attraverso
S vale:
 
q
cos dS
 E  und S   E cosdS  40  r 2 

q
40
q
 d  
0
cos dS
perchè
 d angolo solido
2
r

 
E  un d S 
CASO 2)
q
4 0
 d
Consideriamo una carica q’ esterna
alla superficie chiusa S.
Il flusso del campo elettrico prodotto da q’
attraverso la superficie dS’ è uguale in
valore assoluto ma di segno opposto al
flusso attraverso dS’’ perché l’angolo
solido è uguale per entrambe le aree e
pertanto i flussi si sommano a zero.
LEGGE DI GAUSS
Una carica interna

q
   E  uˆn dA 
o
N cariche interne

1
o
N
q
i 1
i
La Legge di Gauss per il campo elettrico è valida
sempre e costituisce una delle
equazioni di Maxwell (la prima equazione)
Campo di una sfera uniformemente carica
Siano: Q la carica posta nella sfera
a il suo raggio
ra

E
Q
4o r

u
2 r
r
ra

E
Qr 
u
3 r
4o a

ur
Campo di una distribuzione di carica piana
uniforme indefinita
Sia  la densità superficiale di carica

E
2 o
Campo generato da due piani infiniti
uniformemente carichi (con segno opposto)
Siano: Q la carica sui piani
S l’area dei piani
Sia  la densità superficiale di carica
(+  piano a sinistra, -  piano a destra):
Q/S

E
o
Campo elettrico di una distribuzione uniforme
cilindrica di lunghezza infinita
Siano: l la carica per unità di lunghezza
a il raggio del cilindro
l
ra E
20 r
lr
ra E
2
20 a
Conduttore posto in un campo elettrico
In un conduttore immerso in un campo elettrico
esterno le cariche elettriche libere di muoversi
vengono spinte dalla forza del campo elettrico
fino ad addensarsi sulle superfici finché il
campo che esse producono all’interno del
conduttore non annulla completamente il campo
esterno applicato, producendo così un equilibrio.
In conclusione:
1) in un conduttore posto in un campo elettrostatico
e che sia in equilibrio elettrico, il campo elettrico
nei punti interni è nullo;
2) il campo elettrico alla superficie di un conduttore
in equilibrio è normale alla superficie
(altrimenti le cariche sarebbero libere di muoversi
fino a raggiungere un equilibrio, campo nullo);
3) l’intera carica elettrica di un conduttore in
equilibrio si trova sulla sua superficie