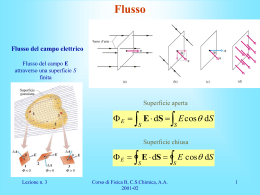
Terza Lezione
Applicazioni del teorema di Gauss, Teorema di
Gauss in forma differenziale, concetti di potenziale
e gradiente
Riassunto della lezione precedente





Dipolo
Esperienza di Millikan
Effetto della materia ed alcune classificazioni
Vettore D
Teorema di Gauss in forma integrale
Esercizio: Distribuzione di carica coassiale
Si supponga di avere un cavo coassiale infinitamente lungo, in cui il
cilindro interno è uniformemente carico, con densità lineare di carica l. Lo
spazio tra i due cilindri è riempito da un mezzo con costante dielettrica e. Si
calcoli il campo tra i due conduttori.

Si applica Gauss ad superficie cilindrica intermedia r di
lunghezza l; il campo elettrico è solo radiale
 

 
 D   ds D  n  Q
D
S
2rlDr  ll
l
Er 

e
2re
Dr

Stesso risultato in assenza di conduttore esterno
a
r
b
Esercizio: Elettrodi Sferici
Elettrodi sferici separati da due strati di materiale dielettrico

Simmetrie radiale: campo radiale

Sfera interna: Q; sfera esterna -Q

Applichiamo il th. Di Gauss ad una
sfera intermedia tra le due
e2
e1
a
c
b
Q
Dr 
4r 2
Q
Er 
4r 2e 1
se
arb
Q
Er 
4r 2e 2
se
brc
Conseguenze Teorema di Gauss

In un conduttore, all’equilibrio non vi è campo: quindi
all’equilibrio non vi sono cariche: del resto le cariche si
respingono, “fuggono” le une dalle altre e si
+
dispongono alla massima distanza
+

In prossimità della superficie vi è una
carica ss Applichiamo il th. Di Gauss
sS
s
Er S 
 Er 
e
e
+
S
+
+
+
+
+
+
+
Esercizio: carica in un guscio sferico

All’interno di un guscio metallico è posta una carica di 1
nC. Qual’è la carica indotta all’esterno? Cosa succede
se il guscio è posto momentaneamente a massa?
+
+
I Teorema di Gauss applicato su
una superficie interna dell’anello:
+
+ E=0, Q=0. La superficie interna ha
-
carica totale -1nC. La superficie
esterna +1nC. NON DIPENDE
DALLA POSIZIONE DELLA
CARICA. Inoltre il campo nel
conduttore è nullo: le cariche
all’esterno si dispongono in modo
indipendente

Se poi si mette momentaneamente
a massa l’esterno del guscio le
cariche esterne vengono rimosse: il
campo esterno diviene nullo (la
carica interna è “schermata”)
+
+ -
-
S
+
-
+
+
Gabbia di Faraday
Da quanto detto, risulta possibile creare uno schermo elettrostatico in un
campo elettrico uniforme (detto gabbia di Faraday) utilizzando come
schermo un involucro metallico (schermo elettrostatico)
Sono presenti cariche elettriche indotte sulla superficie esterna dello schermo
(La carica totale è nulla)

Il campo elettrico all’interno dello schermo è nullo
(Le linee di campo all’esterno sono modificate)

Lo schermo elettrostatico protegge dalle scariche elettriche
-
+
-
E=0
-
+
+
+
+
+
+
+
Sistemi a simmetria piana
Superficie gaussiana = cilindro retto chiuso di
base A perpendicolare alla lastra
Il flusso vale:
 E   EdS  2 EA
S
Il teorema di Gauss dice che:
2 EA 
Q
e0
Quindi, usando la densità superficiale di carica, si
ha:
s
E
2e 0

GIA’ LO SAPEVAMO: calcolato come caso
limite per in disco carico molto grande
Doppia Piastra
Si considerino due piastre infinite, una con carica superficiale +s ed una con carica
-s e le si avvicinino come in (c)
Come nel caso precedente, si sceglie come superficie gaussiana un cilindro retto
chiuso di base A perpendicolare alla lastra. All’interno del cilindro la carica totale è
nulla (essendo le due densità di carica uguali ed opposte) per cui esternamente al
doppio strato E=0. Tra le due piastre, invece, si ha un contributo di campo elettrico
E=s/2e0 diretto da sinistra a destra (perché uscente) dovuto alla piastra carica
positivamente ed un contributo di campo elettrico E=s/2e0 diretto ancora da sinistra
a destra (perché entrante) dovuto alla piastra carica negativamente. Per cui, il
campo totale vale E= s/e0
Piano conduttore carico
Consideriamo ora un piano metallico con distribuzione di carica s. In pratica, a
differenza di prima, dove consideravamo una lamina o un foglio, ora immaginiamo
il piano conduttore estendersi indefinitamente
E
Cilindretto su cui applichiamo il th di Gauss
+ + + ++ + + + + ++ +
Evidentemente la superficie del cilindretto immersa nel conduttore ha flusso nullo:
l’unico contributo non nullo è attraverso la superficie superiore, per cui, il campo
totale vale E= s/e0
Simmetria Sferica


Campo elettrico esterno indistinguibile
da quello che si avrebbe se tutta la
carica fosse concentrata nel centro
(analogo gravitazionale)
Campo elettrico interno, caso
distribuzione uniforme di volume r
4r r 3
q' (r )   rdV  r  dV  rV (r ) 
3
0
0
tuttavia
4
4 3
3
Q  r R  r  Q /  R   q' (r )  Qr / R 3
r
r
3
3
E 
 E  dA 
A( r )
 EdA  E
A( r )

2
dA

EA
(
r
)

4

r
E

A( r )
q
r
E
4e 0 R 3
Teorema di Gauss in forma differenziale
 
d x1  E  nds  E x dy dz
d x 2   E x ' dy dz
z
E
n’=-x
d x1  d x 2  ( E x  E x ' )dy dz
E x
E x
 dEx dy dz 
dxdydz 
dv
x
x
n=x
dv
E’
y
 Ex E y Ez 
dQ rdv
dv 
 dtot  



x
y
z 
e0
e0

d tot E x E y E z r





dv
x
y
z e 0

 r
 Div(E)    E 
e0
dx
dy
x


per D invece Div(D)    D  r
Teorema della Divergenza

Integriamo a destra e a sinistra il teorema di Gauss in
forma differenziale

   Ddv   rdv  Q
V

V
Confrontiamo con il teorema di Gauss in
forma integrale e otteniamo
 

D

n
ds



D
dv


S
V
Esercizio
Dato un campo vettoriale F(r), calcolarne il flusso attraverso la
superficie di un cubo di lato 2a centrato nell’origine e verificare
che il teorema della divergenza è soddisfatto


F  xu x

z
Flusso non nullo solo sulle due facce
y
 
2
2
3
F

n
ds

F
(
a
)
4
a

F
(

a
)
4
a

8
a

x
S
 
F  F 1
x

3


F
dv

V

8a

V
2a
Conservatività del Campo Elettrostatico

Calcoliamo il lavoro per portare q2 da A a B, essendo q2 nel
campo prodotto da q1. Se definiamo dl un tratto infinitesimo del
percorso, tale da poterlo considerare localmente rettilineo:
dW  F  d l
B
 
W AB    F  d l
A
W AB  
1
4e 0
B
dr
B
q1 q2 
A
dl


ur  dl

2
r
r
A
 1 1
dr
1

q1 q2  2  
q1 q2    
4e 0
r
4e 0
 rB rA 
A
1

B
q2
q1
Dipende solo dai punti A e B e non dal percorso seguito
l


Potenziale

Per un campo conservativo è sempre possibile definire un
POTENZIALE, ovvero una grandezza che dipende solo dalla
posizione nello spazio
 
   F  d l  U A  U B  U
B
WAB
A

V U / q1 Potenziale Elettrosta tico
W AB B  
 U
  E  d l  V A  VB  V 
q
q1
A
Se esiste una ddp tra due punti, siamo in presenza di un campo
si misura in Volt [V]=[J/C]; nota che E è misurato in N/C cioè V/m
Superfici Equipotenziali


Sono definiti come luogo dei punti a potenziale
costante
sono sempre ortogonali alle linee di forza
Campo uniforme
Carica puntiforme
dipolo
Il concetto di Gradiente

Calcoliamo il prodotto scalare di E ed elemento infinitesimo di
spostamento, per esempio lungo x
E


E  dx  E dx cos   E x dx  dV
dV
Ex  
dx
V
V
Ex  
;Ey  
...
x
y

dx
Ex



 
E  E x u x  E y u y  E z u z  V

Il campo elettrico diviene funzione di uno scalare!!
Promemoria
Fin qui abbiamo definito due “operatori differenziali”:

La Divergenza (indicata con Div oppure   )

essa associa ad un campo vettoriale una funzione scalare
 


F 
Fx  Fy  Fz
x
y
z

Il gradiente (indicato con Grad oppure 

“nabla”)
essa associa ad una funzione scalare un campo vettoriale
V 
V 
V 
V 
ux 
uy 
uz
x
y
z
Promemoria
Notate come il simbolo della divergenza sia molto informativo:
Nel calcolare   F facciamo effettivamente un prodotto
scalare tra l’operatore gradiente ed il campo: infatti il gradiente
è una sorta di vettore speciale (un operatore appunto…) che ha
bisogno di avere qualcosa alla sua destra su cui “operare”: ha
tre componenti che sono in realtà derivate
     
  ux  u y
 uz
x
y
z

F  Fxu x  Fy u y  Fz u z
 


F 
Fx  Fy  Fz
x
y
z
Alcune note




Gli operatori differenziali che abbiamo introdotto,
sono stati scritti in coordinate rettangolari (x,y,z)
Essi assumono forme diverse nei diversi sistemi di
riferimento (cilindrico, sferico ecc.)
In generale li trovate tabellati, da usare
all’occorrenza, o ve li fate spiegare da un professore
di analisi
Gli operatori sono potenti strumenti matematici, con
un’algebra simile a quella delle matrici
Potenziale per una carica puntiforme
  B
V A  V B   E  dr  
B
A
q
2
4
e
r
A
dr
B
q
q



4e r A 4e rB 4e rA
q



Hanno senso solo differenze di potenziale
Uno dei due potenziali è preso come “riferimento”
In questo caso un riferimento comodo è B all’infinito
V (r ) 
q
4e r