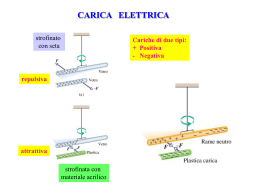
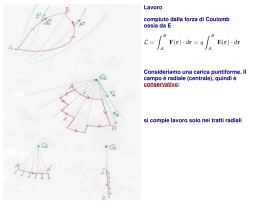
Tabella di riepilogo per una Carica Puntiforme Carica Puntiforme Q Definizione grandezze (scalari e vettoriali) forza di Coulomb campo elettrico energia potenziale (lavoro) FCoulomb qQ rˆ 2 40 r F 1 Q E (r ) Coulomb rˆ 2 q 40 r 1 qQ U (r ) 40 r L qEd Potenziale 1 LAB qQ 1 1 40 rA rB U 1 Q V (r ) q 40 r Legami tra grandezze [ DU DV ] F qE DV E d qQ 1 1 DU 40 rB rA Forza e campo elettrico Campo e potenziale u.m.:V/m [Variazione di energia potenziale] DU LA B DU qDV Energia potenziale lavoro e potenziale L Q 1 1 DV q 40 rB rA [ddp] nota: DV ed L sono riferiti allo stesso cammino AB Obiettivi a metà del I quadrimestre Definizioni Leggi, principi, teoremi Convenzioni Fenomeni, applicazioni Conduttori Isolanti Conservazione della carica Segno delle cariche Elettrizzazione Polarizzazione Forza di Coulomb Quantizzazione della carica Linee di campo Induzione Dipolo elettrico Teorema di Gauss Flusso Distribuzione della carica su un conduttore in equil. Campo elettrico Teorema di Coulomb zero dell’energia potenziale Campo generato da: Linee di campo Flusso del campo elettrico zero del potenziale distribuzioni lineari, distribuzioni piane distribuzioni sferiche Energia potenziale elettrica Potenziale … Potenziale elettrico Superfici equipotenz. Problema generale dell’elettrostatica Densità di carica Capacità e energia di un condensatore è necessario inoltre: conoscere le relazioni esistenti tra le grandezze fisiche definite (e le relative unità di misura!); saper svolgere esercizi che richiedono la semplice applicazione delle definizioni. (come sopra) Buon lavoro e in bocca al lupo per la verifica scritta
Scaricare