Una funzione di due variabili è del tipo
z = f(x , y)
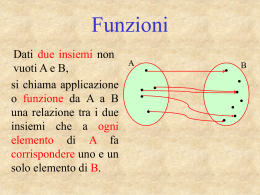
Si definisce funzione reale di due variabili reali una
relazione che associa ad ogni coppia di numeri reali
(x,y) appartenenti al Dominio uno ed un solo numero
reale z
Assegnando a x e y due valori del Dominio si ottiene il
valore di z e, quindi, il punto P(x ; y ; z)
x
y
Esempio:
z = 3x-y+9
Se x = 2 e y = 7 si ottiene z = 8
Il punto è P(2 ; 7 ; 8)
z
Questo punto può essere rappresentato nello “spazio”
P(2 ; 7 ; 8)
8
P
2
7

Il Dominio di una funzione in due variabili è
l’insieme dei valori che possiamo dare a X e Y
affinché Z abbia un valore REALE.
Rx R = R²
Per determinare il dominio di una funzione a
due variabili e’ necessario procedere alla sua
classificazione:
 Funzione intera o Funzione Fratta.


Funzione razionale o irrazionale.
Funzione trascendente : logaritmica o
esponenziale.
D: {R²}
D: {R²| g(x)≠0}
D: {R²} Con n dispari (n:
radicando).
D: {R²|f(x)≥0} Con n
pari.
D: {R²| g(x)≠0} Con n
dispari.
D: {R²|f(x)/g(x) ≥0 U
g(x)≠0} Con n pari.
de Bonis Fara
Vento Diletta
Mastrobattista Francesca