FUNZIONI
MATEMATICHE
ELENA SPERA
y=[(x+1)/(x-1)]^2
2,5
2,0
1,5
1,0
0,5
0,0
-15
-10
-5
0
5
10
15
1
Introduzione

Lo studio delle funzioni permette di interpretare la variazione di
due grandezze, l’una rispetto l’altra, quando tra le due esiste un
legame di tipo matematico.
La teoria dell’analisi delle funzioni è utilizzata in tutte le
materie scientifiche

Dall’esame del grafico di una funzione si possono dedurre molte
proprietà come ad esempio:






se in un certo intervallo la funzione è sempre crescente o
decrescente;
per quali valori delle variabili è definita;
quali sono gli eventuali massimi e minimi che essa assume;
in quali punti interseca gli assi cartesiani;
se è simmetrica rispetto agli assi o all’origine degli stessi;
altro.
2
DEFINIZIONE DI FUNZIONE MATEMATICA

è una relazione di tipo matematico (addizione,
sottrazione, moltiplicazione, divisione, estrazione
di radice, potenza, ecc..), che ad un qualunque
valore x (variabile indipendente), fa
corrispondere una ed una sola y (variabile
dipendente).
A
X
f
Y
B
Ad ogni x di A corrispondono immagini y di B.
3
FUNZIONI BIUNIVOCHE INVERTIBILI
LA FUNZIONE BIUNIVOCA è quella funzione in cui
si verifica che ad ogni y corrisponde una ed una sola
x come ad ogni x corrisponde una ed una sola y.
f
A
B
x
y
f
-1
Le funzioni biunivoche sono invertibili
LA FUNZIONE INVERSA della f(x), detta f-1(x), è la
funzione che agli elementi dell'insieme B associa
uno ed un solo elemento dell'insieme A.
4
DOMINIO E CODOMINIO DI UNA FUNZIONE
 L'insieme A, costituito da tutti i valori che può
assumere la variabile indipendente x, si chiama
DOMINIO della funzione o CAMPO DI
ESISTENZA e dipende dal tipo di legame
(espressione matematica) che c'è tra la x e la y.
Mentre le immagini y corrispondenti alle x di A
sono contenuti in un insieme B che si chiama
CODOMINIO.
DOMINIO
X
f
Y
CODOMINIO
 Il DOMINIO di una funzione è costituito
dall'insieme dei valori reali che può assumere
la x affinché si possa determinare il
corrispondente valore della y.
5
CLASSIFICAZIONE DELLE FUNZIONI
Le funzioni analitiche, che noi studiamo, si possono dividere in due grandi
classi:
ALGEBRICHE (quando il legame tra x e y si riduce ad una equazione
algebrica di grado qualunque):
- f. razionali intere
y=x3+3x2-7
- f. razionali fratte
y=
- f. irrazionali
y=
x 1
x 1
2x 3  3
TRASCENDENTI (funzione non algebrica):
- f. goniometriche
y= senx
f. logaritmiche
y=log x
- f. esponenziali
y= ax
(a>0; a=1)
6
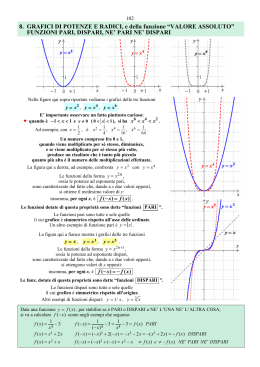
DEFINIZIONE DI FUNZIONE PARI - DISPARI

Definizione di funzioni pari:
una funzione si dice pari quando f(x)=f(-x) qualunque x
reale; tali funzioni sono simmetriche rispetto all'asse y.
Definizione di funzioni dispari:
una funzione si dice dispari quando f(-x)= - f(x) qualunque x
reale; tali funzioni sonno simmetriche rispetto all'origine degli
assi.
y
y
f. pari
x
x
f. dispari
7
GRAFICO DI UNA FUNZIONE

Fissato nel piano un sistema di riferimento XOY cartesiano
ortogonale e data la y=f(x) definita in un certo intervallo di estremi
(a;b), attribuendo alla x dei valori, di volta in volta, variabili tra a e b
possiamo calcolare, in base al legame espresso nella funzione, la y
corrispondente. Ogni coppia x e y individua nel piano un punto della
curva.
Per x= x1--------->f(x1)=y1-----------> P1(x1;y1)
Per x= x2--------->f(x2)=y2-----------> P2(x2;y2)
.
.
.
Per x= xn--------->f(xn)=yn-----------> Pn(xn;yn)

y
P11
P2
Pn
x
La curva passante per tutti i punti calcolati rappresenta il grafico
della funzione espressa dalla legge y=f(x).
8
INTERSEZIONI CON GLI ASSI

Le coordinate dei punti di intersezione del grafico
di una funzione con gli assi cartesiani si
determinano risolvendo l’equazione che si ottiene
ponendo nella equazione y=f(x)

x=0
(per l’intersezione con l’asse y)

y=0
(per l’intersezione con l’asse x)
yY
(x2;0) x
(x1;0)
(0;y1)
9
DETERMINAZIONE DEL SEGNO DI UNA
FUNZIONE

Per determinare il segno di una funzione,
ovvero per quali valori della x essa
assume valori positivi o negativi
all'interno del C.E., basta risolvere la
disequazione f(x)>0.
10
DETERMINAZIONE DEL CAMPO DI
ESISTENZA

Funzioni razionali intere

Sono definite qualunque valore assume
la x (perché le operazioni presenti nella
funzione si possono eseguire qualunque
è il valore della x, e quindi si può
determinare sempre il corrispondente y).

Y= 4x4-3x2+1
C.E.  x  R 
11
DETERMINAZIONE DEL CAMPO DI
ESISTENZA

Funzioni razionali fratte

Sono definite qualunque valore assume la x
tranne che per i valori che annullano il
denominatore (perché le operazioni presenti
nella funzione si possono eseguire solo se il
denominatore è diverso da zero, in caso
contrario non esiste il corrispondente y).

x 1
y 2
x 1
C.E.  x  R-{1} 1) (1; 
12
DETERMINAZIONE DEL CAMPO DI
ESISTENZA

Funzioni irrazionali

In questo caso bisogna vedere se l'indice del radicale è pari o
dispari. Se è pari allora sono definite qualunque valore
assume la x tranne che per i valori che rendono il radicando
negativo; se è dispari sono definite qualunque valore assume
la x. Quindi:

radicale con indice pari
C.E. si ha risolvendo
RADICANDO > 0
radicale con indice dispari C.E. si ha x R


y  x2 1
C.E.  x  R1) (1; 
13
DETERMINAZIONE DEL CAMPO DI
ESISTENZA

Funzioni composte

Quando
la) funzione è composta,
(;
sarà necessario risolvere un
sistema che includerà tutte le
imposizioni fatte per ciascun tipo di
funzione.
14