Funzioni
Funzioni
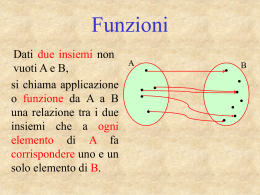
Una funzione di A in B è una relazione che ad
ogni elemento del primo insieme A associa uno
ed un solo elemento del secondo insieme B.
L’insieme A si chiama dominio della funzione.
L’insieme B si chiama codominio della funzione.
Funzioni
A
2
B
4
f: A  B
x > y = f(x)
6
y è l’immagine di x
1
2
Il sottoinsieme di B
costituito da tutte le
immagini degli elementi
di A è detto immagine del
dominio Im (A).
Dominio: A
Codominio: B
Immagine di A: {2,4}
Funzioni
Una funzione di A in B è una relazione che ad
ogni elemento del primo insieme A associa uno
ed un solo elemento del secondo insieme B.
A
2
1
4
2
6
B
Funzioni
Una funzione di A in B è una relazione che ad
ogni elemento del primo insieme A associa uno
ed un solo elemento del secondo insieme B.
A
2
1
4
2
6
B
Rappresentazione grafica
Tabella a doppia entrata
A
B
3
2
(2,3)
B
Rappresentazione cartesiana
3
2
A
Grafico di funzione
A
2
B
1
4
2
f: A  B
x > y = f(x)
6
Si definisce grafico di una funzione f
{(x,y)|xA  y=f(x)B}  AxB
B
4
Rappresentazione cartesiana
2
1
2
A
Funzioni
Analitiche
Razionali intere
Razionali fratte
Irrazionali
Trascendenti
Valore assoluto
Empiriche
logaritmiche
esponenziali
trigonometriche
Funzioni da R in R
Il dominio ed il codominio della funzione sono R
o un intervallo di R.
Sia f la funzione che associa ad ogni
numero il suo inverso.
½
A
2
¼
4
6
B
f: A  B
x > y = f(x)
1
y
x
Funzioni da R in R
Sia f la funzione che associa ad ogni
numero il suo inverso.
Dominio D: {2,4}
A
Im(D): {½,¼}
0
½
2
¼
4
0
B
f: A  B
x > y = f(x)
1
y
x
Funzioni da R in R
Sia f la funzione che associa ad ogni
numero il suo inverso.
f: D=R\{0}  R
x
> y = f(x)
1
y
x
Im(D)=R\{0}
Funzioni da R in R
Razionali intere
Funzioni lineari
y = mx
y = mx+q

polinomi
Rette
Funzioni da R in R
Due grandezze sono direttamente
proporzionali se il loro rapporto è costante.
Retta per l’origine
y = mx
y
m
x
Funzioni da R in R
Razionali intere

Parabole
y = ax2+bx+c
y = ax2
polinomi
Funzioni da R in R
Razionali intere
y = x3

polinomi
y = x4
Funzioni da R in R
Razionali fratte
Dominio: R\{punti che annullano il denominatore}
1
y
( x  1)( x  2)
Funzioni da R in R
Due grandezze sono inversamente
proporzionali se il loro prodotto è costante.
Iperbole equilatera
1
y
x
y∙x = m
Funzioni da R in R
Irrazionali

radici
Radici di indice pari
Dominio: { R | l’argomento della radice ≥ 0}
y  x 1
Funzioni da R in R
Irrazionali

radici
Radici di indice dispari
Dominio: R
y  3 x2
Funzioni da R in R
Valore assoluto
se x-1≥0
x 1
y  x 1  
( x  1) se x-1<0
Funzioni pari
Una funzione si dice pari se xD f(x)=f(-x).
y = ax2
Le funzioni pari sono simmetriche rispetto
all’asse delle ordinate.
Funzioni dispari
Una funzione si dice dispari se xD f(x)=-f(-x).
y = ax3
Le funzioni dispari sono simmetriche rispetto
all’origine.
Funzioni periodiche
Una funzione si dice periodica di periodo T se
f(x)=f(x+kT).
y = sin x
ye
sin x
sin x
y
1  cos x
T=2π
Funzione crescente
Una funzione si dice crescente se x1, x2 D,
x1 > x2  f(x1) > f(x2)
y 3
x 1
Funzione decrescente
Una funzione si dice decrescente se x1, x2 D,
x1 > x2  f(x1) < f(x2)
1
y
x
Funzioni monotòne
Una funzione si dice monotòna in un intervallo
ID se è sempre crescente o decrescente in I.
Una funzione si dice monotòna se è sempre
crescente o decrescente in D.
Funzioni monotòne
Una funzione si dice costante in un intervallo
ID se f(x)=c, xI, cR.
Una funzione si dice costante se f(x)=c, xD.
y=3
retta parallela
all’asse delle x.