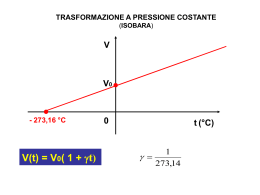
GAS PERFETTI E GAS REALI ALL’EQUILIBRIO
IDEAL VS REAL GAS
Antonio Ballarin Denti
[email protected]
LA LEGGE DI BOYLE
(Robert Boyle 1627-1691)
Le variabili di stato che descrivono le proprietà di un gas sono:
volume (V), pressione (P) e temperatura (T)
Il volume occupato da una data massa di gas, a temperatura
costante, è inversamente proporzionale alla pressione
P
La trasformazione da
A(pA, VA) a B(pB, VB)
è isoterma e la curva
PV = k è un’iperbole
A
B
V
I LEGGE DI GAY-LUSSAC
(p = cost)
Trasformazione isobara
Relazione lineare
II LEGGE DI GAY-LUSSAC
(V = cost)
Trasformazione isocora
Relazione lineare
P
P0
T
Anche le superfici si espandono con T
Sia A0 = L0 × L0 a T0. Alla temperatura T si avrà:
Trascuriamo
poiché α << 1
Posto T0 = 0
Posto 2α = β
β è il coefficiente di espansione planare
Per i volumi si definisce un coefficiente di dilatazione volumetrica γ
(per T0 = 0)
(per 3α = γ)
Per i gas (a pressione costante) vale la I legge di Gay Lussac:
[K-1]
I GAS PERFETTI – EQUAZIONE DI STATO
PROPRIETÀ DEI
GAS PREFETTI
-IL NUMERO DELLE SUE MOLECOLE è GRANDE
-IL GAS È RAREFATTO (NO INTERAZIONI TRA MOLECOLE)
-LA SUA TEMPERATURA È >> DELLA T DI LIQUEFAZIONE
Troviamo l’equazione di stato. Nella I legge di Gay-Lussac si ha:
Passando alla temperatura assoluta (t = T-273)
AB
P
P
C
B
P0
*
A
BC
V
V0’
V0
**
Sostituendo * in ** 
Il prodotto pressione-volume è proporzionale alla T assoluta
LA MOLE E IL NUMERO DI AVOGADRO
Definizioni:
I pesi atomici sono le masse degli atomi espresse
In un’unità di misura definita come la dodicesima
parte della massa del I12C
Analogamente si definiscono i pesi molecolari
Mole è la quantità di materia la cui massa espressa
in grammi è uguale al peso atomico (o molecolare)
Il numero di atomi in una mole è il numero di Avogadro
NA = 6.02 × 1023
LA LEGGE DI AVOGADRO
“una mole di gas a qualunque p e T costanti
occupa sempre lo stesso volume (volume molare)”
VM=22.414 litri
P0 e 273 sono termini fissi, V0 sarà proporzionale
al numero di moli del gas. Possiamo porre:
R è la costante dei gas perfetti:
L’equazione di stato dei gas perfetti diventa dunque:
Dove m è la massa del gas
ed M il suo peso molecolare
COMPORTAMENTO DEI GAS REALI
Scostamento della funzione pV = f(p) dal suo valore in base alla legge di Boyle
PV
Solo nei punti a derivata 0
T =500 K
(punti di Boyle) abbiamo
pV = cost.
Il gas è meno compressibile
400
ad alte pressioni. A basse T
la compressione determina
300
la liquefazione del gas
200
P (atm)
COMPORTAMENTO DEI GAS REALI
Un’isoterma reale si compone di 3 parti:
n
1. Il tratto ad (basse pressioni)
tipico della legge di Boyle
2. Il tratto orizzontale ba tipico
del processo di liquefazione
3. Il tratto bn fortemente
ascendente tipico dello
stato liquido(incomprimibile)
L+V
C è il punto di rugiada
(comincia la liquefazione)
I GAS REALI
Per un gas perfetto vale
U=T
Per un gas reale invece si ha:
U= T + V
energia interna
del gas reale
energia cinetica
del moto di
agitazione termica
un’energia potenziale,
tanto maggiore quanto
più lontane sono le sue
molecole
Inoltre le molecole di un gas reale non sono
puntiformi e hanno quindi volume non nullo
Date queste differenze possiamo vedere come
diventa l’equazione di stato per un gas reale
Consideriamo che per un gas perfetto vale:

V/M è il volume specifico VS
Van der Waals modifica questa espressione e
ottiene l’equazione di stato per i gas reali:
Effetto delle interazioni molecolari
Termine di covolume,
tiene conto del fatto
che le molecole hanno
un volume proprio
Mescolando vari gas si ha:
Con ni = numero moli dei singoli gas, i= 1,..,n
Per ogni singolo
gas vale :
pi = pressione
parziale
Sommando su tutti i costituenti:
Vale quindi la Legge di Dalton