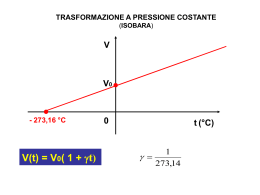
A differenza degli stati liquido e solido, quando un
corpo si trova allo stato gassoso tende a
occupare tutto il volume a disposizione
GAS
Leggi dei gas

Leggi fisiche che descrivono il comportamento
dei gas in funzione delle variabili di stato, quali
volume, temperatura e pressione.
Le particelle gassose hanno energia cinetica
maggiore dell'energia di attrazione, perciò
tendono ad occupare tutto lo spazio disponibile.
Lo
stato
gassoso
possiede
diverse
proprietà:
•Bassa viscosità
•Mancanza di forma e volume propri
•Alta comprimibilità
•Completa miscibilità tra loro
•Esercizio di una pressione sulle pareti
1 proprietà estensive: massa, volume
Le proprietà estensive dipendono dalla quantità di
sostanza
2 proprietà intensive: temperatura, pressione
Caratteristiche come composizione, struttura, stato
di aggregazione, sono dette proprietà intensive e
dipendono dalla natura delle sostanze ma non dalla
loro quantità
La Pressione è una Forza per unità di superficie,
ed è data semplicemente dal rapporto P=F/S
quando F è uniformemente distribuita su S.
Nei gas la pressione è legata agli urti delle
particelle contro le pareti del recipiente.
La pressione si valuta generalmente misurando
l'altezza di una colonna di mercurio (Hg) che il
gas riesce a sostenere contro la forza di gravità.
Al livello del mare e a 0° C, la pressione
atmosferica media fa salire la colonna di Hg a
760 mm
La pressione si misura in :
•Pascal (SI)
•Atmosfere
•mmHg o Torr
1 torr= 133,322 Pa
1 atm=101325Pa
Leggi dei gas valide per gas perfetti in cui le molecole hanno
dimensioni puntiformi e non vi sono forze intermolecolari
Relazione tra volume di un gas e
pressione a T=costante
Legge di Boyle P1V1=P2V2 ; PV = K
A pressione costante, il volume di un gas è
proporzionale alla temperatura e aumenta di
1/273(a) del volume che occupa a 0°C, per
ogni aumento della temperatura di 1°C.
V=Vo(1+at)
Da questa evidenza esigenza di definire un
valore di temperatura che corrisponda a -273° C.
In base a tale valore, detto zero assoluto, è stata
stabilita la scala della temperatura assoluta
(Kelvin).
A pressione costante il volume di un gas cresce con il crescere
della temperatura Legge di Charles
V1/V2= T1/T2 ; V/T= K
Temperatura assoluta
In °K
Analogamente, a volume costante la pressione di un
gas cresce al crescere della temperatura (legge di Gay
Lussac):
P1/P2= P/T = cost
Effettuando in successione una trasformazione isocora
ed una isoterma e applicando le relative leggi, si arriva
alla relazione valida quando cambiano tutte e tre le
variabili
PV/T = cost =R
Tale relazione è applicabile ai gas perfetti
considerando:
•Molecole puntiformi
•Assenza di interazioni
Per definire uno stato di un gas perfetto, sono necessarie e
sufficienti tre variabili macroscopiche, ciascuna suscettibile
di misura diretta: P, V, T legate tra loro dall’ equazione di
stato dei gas perfetti
PV = nRT
P è il valore della pressione del gas;
V è il volume occupato dal gas;
n è il numero di moli del gas;
R è la costante universale dei gas, il cui valore è funzione
delle unità di misura adottate per esprimere le altre
grandezze nell'equazione;
T è la temperatura assoluta del gas, generalmente
espressa in Kelvin.
dove R = 0.082 l atm mol-1 K-1 nel SI
K-1
R = 8.3143 J mol-1
Legge di Avogadro:
" Volumi uguali di gas nelle stesse condizioni di
temperatura e di volume, contengono un ugual
numero di molecole “
Una mole di qualunque gas, alle medesime
condizioni di temperatura e di pressione, occupa
lo stesso volume.
A c.n. questo volume è pari a 22,4 l/mole
La condizioni normali (c.n.) corrispondono a 1
atm e 0°C (273°K)
L'equazione di stato dei gas perfetti descrive bene il
comportamento dei gas reali per pressioni non
troppo elevate e per temperature non troppo vicine
alla temperatura di liquefazione del gas. In questi
casi, una migliore descrizione del comportamento
del gas è dato dall'equazione di stato di Van der
Waals
La legge di Van der Waals è una equazione di stato
che estende la legge dei gas perfetti
(1) PV= nRT
con l'introduzione di due valori a e b (costanti di
Van der Waals) che dipendono dalla sostanza in
esame.
La legge generale dei gas si applica
correttamente solo al gas ideale o perfetto,
costituito di particelle tutte uguali, con la stessa
massa e con volume nullo (puntiformi) e non
interagenti: è un modello che è stato costruito
per razionalizzare il comportamento dei gas.
Un gas reale è invece caratterizzato da
particelle con un volume definito; se si vuole
perciò applicare la legge dei gas a gas reali è
necessario introdurre delle correzioni.
Di un gas reale, per esempio, si può esaminare
il fattore di comprimibilità Z
La formulazione della legge di Van der Waals è la seguente:
(2)
Dove p è la pressione del gas, n la quantità di sostanza (numero di
moli),V il volume occupato, R la costante universale dei gas e T la
temperatura assoluta.
La presenza di forze attrattive tra le molecole ha l'effetto di ridurre la
pressione che il gas esercita sulle pareti del contenitore e la pressione
viene ridotta di una quantità che è proporzionale 1/V²
al volume V il "volume libero" V - n b, dove b è il volume molare
"escluso", cioè il volume propriamente occupato dalle molecole di una
mole di gas
Nel gas perfetto non esiste volume escluso, ovvero le molecole sono
immaginate come puntiformi.
Teoria cinetica dei gas
Ecin= ½ m v2
v= velocità media delle molecole
Per i gas perfetti:
PV = 1/3 N m v2
N= numero di molecole
v2 = velocità quadratica media
Per una mole di gas: PV = 1/3 NA m v2  PV = 2/3 NA (½ m v2) 
PV = 2/3 NA Ecin
PV = RT  RT = 2/3 NA Ecin  Ecin= 3/2 RT/NA  Ecin= 3/2 kT (per
una molecola)
(k= costante di Boltzmann= R/NA= 1.38 10-23 J K-1)
Ecin mol= 3/2 RT (per una mole)
L’energia cinetica di un gas ideale dipende solo dalla T assoluta ed è
indipendente da P, V e dalla natura del gas
A T=0 °K il moto di traslazione molecolare cessa
Distribuzione delle velocità
molecolari (Maxwell)
Maxwell valutò statisticamente la distribuzione delle
velocità nelle particelle di gas con la funzione di
distribuzione di velocità che esprime la frazione di molecole
DN/N che possiedono una certa velocità. A T più alte la
velocità media è + bassa e aumenta la frazione di molecole
con velocità che si avvicinano alla massima
v
v media
velocità più probabile
Un barometro a mercurio
Legge di Graham= velocità di fuoriuscita di un gas da un piccolo
foro inversamente proporzionale al suo PM
v1/v2= t2/t1 = √PM2/ √PM1
MISCELE di GAS
Se il sistema è costituito da una miscela di due o
più gas che occupano lo stesso volume V,
identificando ogni singola specie gassosa con i
simboli A, B, ..i... e considerando che tutti si
comportino come gas ideali, ognuno di essi seguirà
la legge generale.
Pressione parziale del gas i :
pressione che il gas i eserciterebbe se occupasse
da solo tutto il volume disponibile, dato che,
considerando gas ideali, le particelle sono
indistinguibili tra loro.
Dati due gas A e B
Legge di Dalton
P = PA+PB
Per i gas in miscela
P= ∑Pi = ∑ni RT/V=
Pi/P= ni/ ∑ni =i
Pi= iP
la pressione parziale di un gas i è data dal
prodotto della sua frazione molare i per la
pressione totale.
Volume parziale di un gas= volume che un
gas in miscela con altri occuperebbe se si
trovasse da solo alla stessa pressione totale
V= ∑Vi = ∑niRT/P
Vi=ni/∑ni V= iV
Il rapporto in moli equivale al rapporto in
volume in una miscela di gas
Densità dei gas
Dall’equazione di stato dei gas perfetti
PV =mRT/PM
Si può ricavare la densità di un gas di peso
molecolare PM
d (g/l) = m/V= PM.P/RT
Che è direttamente proporzionale a P e PM e
inversamente alla T
Densità relativa di 2 gas a e b
da/b= da/db= PMa/PMb
Gas reali se sottoposti ad una adeguata pressione e
portati ad una T abbastanza bassa, condensano,
diventando prima liquidi, poi solidi.
passaggio alla fase liquida di un gas reale
Portando in un diagramma P/V (diagramma di
Andrews), i dati relativi si ottengono curve diverse a
seconda delle varie T.
C è detto punto critico ed è identificato da una coppia di valori di P e di V:
PC= pressione critica
VC= volume critico
Il modello cinetico molecolare di
un gas
Tc = temperatura critica del gas al di sopra della
quale non è possibile liquefare il gas, qualunque sia
la P che si impone: il gas resta perciò sempre nel suo
stato gassoso
Le isoterme a T > TC, hanno un andamento simile a
quello dei gas ideali
Per non far reagire Na
metallico violentemente con
l’umidità presente, si aggiunge
KNO3 che produce altro azoto
reagendo con Na
KNO3 +NaK2O + Na2O+ N2
gli ossidi metallici basici
ottenuti reagiscono a loro volta
con biossido di silicio dando un
prodotto vetroso
K2O + Na2O+ SiO2  vetro