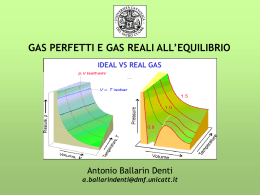
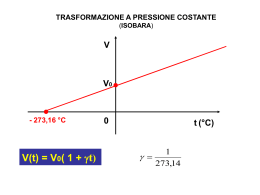
1
La lezione di oggi
Il comportamento microscopico dei gas
Il 1 principio della termodinamica
2
! 
Equazione di stato dei gas
! 
Applicazioni dell’equazione di stato
! 
La teoria cinetica dei gas
! 
Il 1 principio della termodinamica
3
Equazione di stato dei gas ideali
! 
Gas ideale: non ci sono interazioni tra le molecole
! 
Condizioni standard ( T = 20 oC, P= 1 atm )
! 
Gas reale in condizioni standard = gas ideale
Se voglio
aumentare la
pressione P…
Aumento la
temperatura a V
costante
Aumento il numero
di molecole (N)
Equazione di stato
dei gas perfetti
Diminuisco il volume
(V)
P=k
NT
V
4
Equazione di stato dei gas ideali
NT
P=k
V
Equazione di stato
dei gas perfetti
P V = N k T k = 1.38 ⋅ 10
-23
J/K
Costante di
Boltzmann
N: numero di molecole di gas ( ∝ massa)
T in K, P in Pa, V in m3
PV =nRT
n: numero di moli di gas (
T in K, P in Pa, V in m3
∝
massa)
R = kN Avogadro = (1.38⋅10-23 J/K)(6.022 ⋅1023 molecole/mole) = 8.31 J/(mole ⋅ K)
5
Moli e massa molecolare
o 
o 
o 
o 
o 
Unità di massa atomica (u, o uma) è ottenuta assegnando
arbitrariamente 12 u al 12C
1 u = 1 uma = 1.665.10-27 kg
Una mole (o grammo-molecola) ! numero di Avogadro di quantità
elementari (atomi, molecole,....)
Una mole contiene tante quantità elementari quante ce ne sono in 12
grammi di 12C
Una mole è il numero di grammi di sostanza uguale alla massa
molecolare espressa in uma
Problema
Calcolare la massa di una molecola di ossigeno O2
m=
M molecolare ossigeno
N Avogadro
-3
32.0
⋅
10
kg/mole
- 26
=
=
5.32
⋅
10
kg/molecola
23
6.02 ⋅ 10 molecole/mole
massa di 1 mole = 32.10-3 kg
6
! 
Equazione di stato dei gas
! 
Applicazioni dell’equazione di stato
! 
La teoria cinetica dei gas
! 
Il 1 principio della termodinamica
7
Trasformazioni isoterme
Parto dall’equazione di stato dei gas
PV =nRT
Ipotesi:
"  T costante (trasformazione isoterma)
"  Massa costante
Legge di Boyle
Piniziale Viniziale = Pfinale Vfinale
Nel piano PV le isoterme
sono iperboli
PV = k
8
Trasformazione isobara
Parto dall’equazione di stato dei gas
PV =nRT
Ipotesi:
"  P costante (trasformazione isobara)
"  Massa costante
Legge di Charles
Viniziale Vfinale
=
Tiniziale Tfinale
Nel piano VT le isobare
sono rette
V=k.T
#  T = 0, V = 0
#  T = 0 ! zero assoluto
9
! 
Equazione di stato dei gas
! 
Applicazioni dell’equazione di stato
! 
La teoria cinetica dei gas
! 
Il 1 principio della termodinamica
10
La teoria cinetica dei gas
Pressione e temperatura ! grandezze macroscopiche
!  Posizione o velocità di una molecola
! grandezze microscopiche
! 
Come faccio a misurarle ?
o  Macroscopiche: manometro e termometro
o  Microscopiche: ???
o  Teoria cinetica dei gas:
# 
# 
# 
# 
# 
gas ! insieme di molecole
grande numero di molecole identiche
ogni molecola ha massa m ed è
puntiforme
si muovono in modo casuale e
obbediscono alle leggi di Newton
solo urti elastici
11
Teoria cinetica e pressione dei gas
Una molecola di massa m, con velocità v, in un contenitore di volume V urta contro la
parete
Quantità di moto
p i,x = - mv x
Prima dell’urto
p f, x = mv x
Dopo l’urto
Δp x = 2mvx
Variazione
F parete su molecola
causa la Δp
Tempo necessario a fare
andata e ritorno
2mv x mv
F=
=
2L/v x
L
2
x
2L
Δt=
vx
Pressione
media
2a legge di
Newton
 Δp
∑ F = Δt

 Δp
∑ F = Δt
F mv 2x /L mv 2x
P= =
=
2
A
V12
L
Teoria cinetica e pressione dei gas
Distribuzione delle velocità delle
molecole di un gas a due
temperature
(Distribuzione di Maxwell)
Velocità più probabile
Generica velocità in 3 dimensioni
(v2 ) m = (v2x ) m + (v2y ) m + (v2z ) m
2
2
2
Non ci sono direzioni privilegiate (v x ) m = (v y ) m = (vz ) m
2
2
x m
2
y m
2
z m
2
x m
(v ) m = (v ) + (v ) + (v ) = 3 (v )
Nella pagina
precedente
avevamo
ottenuto
mv
P=
V
2
x
Per N
molecole
ovvero
1
(v 2x ) m = (v 2 ) m
3
P / Km
1 m(v2 ) m 2 N
Km
P= N
=
13
3V
3
V
Energia cinetica e temperatura
Equazione dei gas perfetti
+
PV =NkT
1
PV = Nm(v 2 ) m = NkT
3
Pressione nella teoria cinetica
dei gas
1 m(v 2 ) m
P= N
3
V
2 1
N( mv 2 ) m = NkT
3 2
L’energia cinetica media delle
molecole di un gas è proporzionale
alla Temperatura
1
K m = ( mv 2 ) m
2
3
K m = kT
2
Velocità quadratica media
v qm
= (v ) m = 3kT =
m
2
3kT
=
(M/N A )
3N A kT
=
M
3RT
M
14
Esercizio
Qual è l’energia cinetica media di una molecola di gas a 37 C ?
3
3
K m = kT = (1.38 ⋅ 10 -23 J/K)(273 + 37 K) = 6.4 ⋅ 10 −21 J
2
2
Calcolo l’energia cinetica media di una mole dello stesso gas
alla stessa temperatura.
K
1 mole di gas
m
3
= N A ( kT) =
2
(6.02 ⋅10 23 molecole/mole)(6.4 ⋅10 -21 J/molecola) = 3900 J/mole
3700 J sono tanti o pochi ? Prendiamo una pietra di 1 kg e vediamo a che
velocità devo lanciarla per avere questa K ?
2 ⋅ 3900
2K
= 88 m/s = 320 km/h
v=
=
1
m
15
Esercizio
Qual è la velocità quadratica media delle molecole presenti nell’aria
(O2 e N2) a temperatura ambiente (20 C) ?
m(O 2 ) = M O 2 ⋅ (u.m.a.) = (32)(1.66 ⋅ 10 -27 kg) =5.3 ⋅ 10 -26 kg
v qm
3(1.38 ⋅ 10 -23 J/K)(273 + 20)
3kT
= 480 m/s = 1700 km/h
=
=
- 26
5.3 ⋅ 10 kg
m
m(N 2 ) = M N 2 ⋅ (u.m.a.) = (28)(1.66 ⋅ 10 -27 kg) =4.6 ⋅ 10 -26 kg
v qm
3(1.38 ⋅ 10 -23 J/K)(273 + 20)
3kT
= 510 m/s = 1800 km/h
=
=
- 26
4.6 ⋅ 10 kg
m
16
Energia interna di un gas ideale
! 
Energia interna: somma dell’energia potenziale e cinetica
delle molecole che la compongono
! 
U = Σi (Ui + Ki)
! 
Gas perfetto: urti elastici
! 
! 
Ui = 0
Ki = 3/2 kT
3 N
3
3
N A kT = nRT
U = NkT =
2 NA
2
2
Numero di
molecole
Numero di
moli
17
La legge di Dalton (o delle pressioni parziali)
! 
! 
! 
! 
! 
Considero una miscela di due gas perfetti
I due gas non interagiscono/reagiscono tra di loro
Le molecole non interagiscono tra di loro
La pressione è data dagli urti delle molecole sulle pareti
Il contributo alla pressione totale è indipendente per i 2 gas
Gas 1
Gas 2
Gas
(1+2)
N1 k T
P1 =
V
N kT
P2 = 2
V
Ptotale =
Ptotale = P1 + P2
(N1 + N 2 ) k T
V
Legge di Dalton
In una miscela, ciascun gas esercita la pressione che
eserciterebbe se occupasse da solo tutto il volume
18
Esercizio
Un pneumatico viene gonfiato a una pressione relativa di 200 kPa a T=10 C. Dopo
un tragitto di 100 km, la T sale a 40 oC.
Qual è ora la pressione del pneumatico ?
"   n costante (non aggiungo/tolgo aria)
Condizioni a contorno
"   V costante (se varia il volume,
varia di una quantità trascurabile)
PV =nRT
Equazione di stato dei gas
perfetti
Piniziale Pfinale
=
Tiniziale Tfinale
19
Esercizio
PV =nRT
Equazione di stato dei gas
perfetti
Piniziale Pfinale
=
Tiniziale Tfinale
P e T assolute !!!
Tfinale
(273 + 40) K
5
3.01
⋅
10
Pa = 3.3 ⋅ 10 5 Pa = 330 kPa
Pfinale =
Piniziale =
(273 + 10) K
Tiniziale
ΔP Pfinale - Piniziale 3.30 ⋅10 5 - 3.01⋅10 5
29 kPa
=
=
=
≅ 0.10 = 10%
5
P
Piniziale
3.01⋅10
301kPa
La pressione è aumentata del 10% (!non trascurabile !)
20
! 
Equazione di stato dei gas
! 
Applicazioni dell’equazione di stato
! 
La teoria cinetica dei gas
! 
Il 1 principio della termodinamica
21
Il primo principio della termodinamica
! 
! 
! 
! 
Voglio applicare la legge di conservazione dell’energia
Il calore è una forma di energia che viene scambiata
Energia interna: somma di energie potenziale e cinetica di un
sistema
Caso 1: nel sistema entra una quantità di calore Q senza che venga
compiuto del lavoro
Uf = Ui + Q
t = t0
t = t1
t = t2
Convenzione importante
Il sistema acquista calore:
Il sistema cede calore:
ΔU = Uf - Ui = Q
Q>0
Q<0
Uf > Ui
Uf < Ui
22
Il primo principio della termodinamica
! 
Caso 2: il sistema compie un lavoro sull’ambiente esterno
N.B. il sistema è
termicamente isolato $ Q=0
Uf = Ui - L
t = t0
t = t1
t = t2
ΔU = Uf - Ui = -L
Convenzione importante
Il sistema compie lavoro:
Compio lavoro sul sistema:
L>0
L<0
In generale, se Q e L sono entrambi diversi da 0, vale il
Primo principio della
termodinamica
ΔU = Q - L
23
Il primo principio della termodinamica
U, Q, L
Q ! energia che fluisce
per contatto termico
L ! energia trasferita per
azione di una forza che
agisce su una distanza
U dipende dallo stato del sistema (T, P, V)
U ! FUNZIONE DI STATO
Q e L dipendono da come il sistema cambia da uno
stato all’altro
24
Trasformazioni reversibili e irreversibili
! 
! 
! 
! 
! 
Processi quasi-statici: sono molto lenti
Il sistema è sempre in equilibrio con l’ambiente circostante
Il valore di P e T è sempre uniforme in tutto il sistema
Sistemi privi di attrito e forze dissipative
Questi processi sono reversibili ! torno allo stato iniziale
Nella realtà tutti i processi sono irreversibili (attrito,.....),
ma noi faremo sempre l’approssimazione di processi reversibili
25
Trasformazione isobara P = cost
Il gas si
espande
Il gas compie un lavoro L sul pistone
L = F ⋅ (x f - x i ) =
P ⋅ A ⋅ (x f - x i ) =
P ⋅ (Axf - Ax i ) =
L = area sotto la curva che
rappresenta la trasformazione
nel diagramma PV
P ⋅ (Vf - Vi ) = P ⋅ ΔV
Primo principio della
termodinamica
Q = ΔU + P. ΔV
26
Trasformazione isocora
Il recipiente
contiene un
gas
L = F ⋅ (x f - x i ) = 0
Area = 0
Fornisco una
quantità di
calore Q
Il volume
rimane
costante
Trasformazione isocora ! L = 0
Primo principio della
termodinamica
ΔU = Q
27
Trasformazione isoterma
Espansione
isoterma
Equazione dei gas perfetti
PV =NkT
T = costante
P V = costante
costante
P=
V
& Vf
L = NkT ln$$
% Vi
Il lavoro L è l’area
sottesa dalla curva
Nel piano PV la
trasformazione è
descritta da
un’iperbole
#
& Vf
!! = nRT ln$$
"
% Vi
#
!!
"
Nota. Se comprimo il gas,
Vf/Vi<1, ln(Vf/Vi )<0,
L<0, compio lavoro sul
28
sistema
Trasformazione adiabatica
Non ho scambio di calore con l’esterno
Q=0
Compressione adiabatica
Una
compressione
veloce è una
buona
approssimazione
di adiabatica
Espansione adiabatica
P V = costante
γ
29
Il primo principio della termodinamica
Trasformazione
Grandezza costante
In base al primo
principio:
Isobara
P = costante
Q = ΔU + L=
ΔU + PΔV
V = costante
ΔV = 0
quindi L = 0
Q = ΔU
Isoterma
T = costante
ΔT = 0
quindi ΔU = 0
Q=L
Adiabatica
Q=0
ΔU = -L
Isocora
30
Esercizio
n. 72, pag. T124 Walker
Un cilindro dotato di un pistone mobile contiene 2.50 moli di argon a temperatura
costante di 295 K. Quando il gas viene compresso isotermicamente, la sua pressione
aumenta da 101 kPa a 121 kPa.
Trovare:
1.  Il volume finale del gas
2.  Il lavoro compiuto dal gas
3.  La quantità di calore fornita al gas
31
1.  Il volume finale del gas
Equazione dei gas perfetti
PV =nRT
R = 8.31 J/(mol ⋅ K)
n R T 2.5 ⋅ (8.31) ⋅ (295)
-2
3
Vf =
=
=
5.1
⋅
10
m
Pf
121 ⋅ 10 3
2.  Il lavoro compiuto dal gas
& Vf
L = nRT ln$$
% Vi
& Pi
L = nRT ln$$
% Pf
#
& Pi
!! = nRT ln$$
"
% Pf
#
!!
"
#
& 101 ⋅ 10 3
!! = (2.5) ⋅ (8.31) ⋅ ln$$
3
121
⋅
10
%
"
#
!! = - 1.1 kJ
32
"
3.  La quantità di calore fornita al gas
1 principio della
termodinamica
ΔU = Q - L#
Q = ΔU + L = 0 + (-1.1 kJ) = - 1.1 kJ
33
Riassumendo
La conservazione dell’energia
porta alla formulazione del
1 principio della termodinamica
34