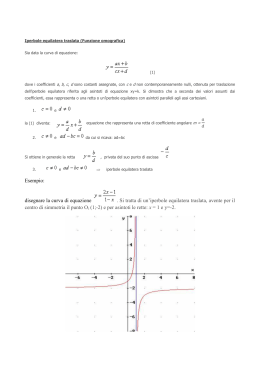
Rappresentazione delle CONICHE
Si definisce conica una curva del piano avente equazione del tipo f(x,y) = 0, dove
f(x,y) è un polinomio a coefficienti reali di secondo grado nelle variabili x e y
L’equazione generale della conica è:
ax2 + bxy + cy2 + dx + ey + f =0
dove a, b, c, d, e, f, sono numeri reali e almeno uno tra a, b, c, è diverso da zero
•
se b2 - 4ac < 0
ho un ELLISSE
•
se b2 - 4ac = 0
ho una PARABOLA
•
se b2 - 4ac > 0
ho un IPERBOLE
Rappresentazione delle CONICHE
PARABOLA (asse parallelo all’asse delle ordinate)
L’equazione generale:
•
ASSE
•
VERTICE
y = ax2 + bx + c
b
x
2a
 
 b
  ; 
 2a 4a 
•
FUOCO
 b 1  
 ;

 2a 4a 
•
DIRETTRICE
 b 1  
  ;

4a 
 2a
Rappresentazione delle CONICHE
Esempi:
y = 4x2 + 3x + 2
y = 4x2 + 2
Rappresentazione delle CONICHE
CIRCONFERENZA
L’equazione generale:
•
x2 + y2 + ax + by + c = 0
CENTRO
 a b
  ; 
 2 2
RAGGIO
1 2
 a  b
r        c 
a  b 2  4c
2
 2  2
2
•
•(x - x0)2 + (y - y0)2 = R2
CIRCONFERENZA equazione parametrica:
• x = R cost
• y = R sent
2
Rappresentazione delle CONICHE
Esempi:
x2 + y2 -25 = 0
6x2 + 6y2 - 36x - 36y – 72 =0
Rappresentazione delle CONICHE
ELLISSE
L’equazione generale:
x2 y2
 2 1
2
a
b
Equazione ELLISSE con centro diverso
b
-a
dall’origine degli assi:
a
-b
( x  x0 ) 2 ( y  y0 ) 2

1
2
2
a
b
ELLISSE equazione parametrica:
• x = a cost
• y = b sent
Rappresentazione delle CONICHE
Esempi:
x2 y2

1
25 9
Rappresentazione delle CONICHE
Esempi:
2x2 + y2 - 4x + 6 y=0
Centro (1,-3)
Semiassi
11
a
2
b  11
Rappresentazione delle CONICHE
IPERBOLE
L’equazione generale:
x2 y2
 2 1
2
a
b
Equazione IPERBOLE con centro
diverso dall’origine degli assi:
-a
a
( x  x0 ) 2 ( y  y0 ) 2

1
2
2
a
b
asintoti
b
y x
a
Rappresentazione delle CONICHE
IPERBOLE EQUILATERA
a=b
x2 y2
 2 1
2
a
a
x2  y 2  a2
asintoti
-a
y  x
a
Esempio: x 2
 y2  4
Rappresentazione delle CONICHE
IPERBOLE EQUILATERA con asintoti paralleli agli assi coordinati
xy  k