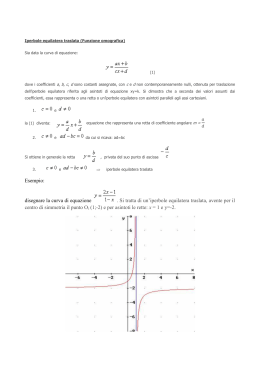
L’iperbole
Teoria e laboratorio
Lavoro di gruppo realizzato da:
Vensy Valentini
e
Roberta Salerno
Sommario

La sezione conica
 Il luogo geometrico
 Simmetrie
 L’equazione cartesiana
 Caratteristiche dell’iperbole
 Asintoti
 Eccentricità
 Iperbole equilatera
 L’iperbole in generale
 Rappresentazione grafica di una iperbole e
del suo asintoto
La sezione conica
L’intersezione tra la
superficie conica a due
falde e un piano, non
passante per il vertice,
che formi con l’asse un
angolo minore della
semiapertura
della
superficie conica è
un’iperbole.
( Apollonio di Perga (262 a.C.- 190 a.C.) )
Il luogo geometrico
Siano fissati due punti F1 del
piano (detti fuochi) ed il
parametro reale positivo a, si
dice iperbole il luogo geometrico
dei punti P del piano per i quali
la differenza (in valore assoluto)
delle distanze da F1 e F2 è
costante e uguale a 2a, ovvero
tale che sia:
| PF1 – PF2 | = 2a
La distanza tra i due fuochi è
chiamata distanza focale e
viene indicata con 2c.
( René Descartes (1596- 1650))
Simmetrie
 La
retta passante per i due fuochi e la
retta a questa perpendicolare nel punto
medio di F1F2 sono assi di simmetria
per l’iperbole
 Il punto medio del segmento F1F2 è
centro di simmetria per l’iperbole.
L’equazione cartesiana

Sulla base della definizione del
luogo geometrico, sviluppando i
calcoli, si ottiene l’equazione
cartesiana
dell’iperbole.
In
particolare
ci
occuperemo
dell’iperbole avente per assi di
simmetria gli assi cartesiani con i
fuochi sull’asse x ed equidistanti
dall’origine.
In tal caso si ottiene l’equazione
canonica o normale:
x2 – y2
a2 b2
= 1
con a = semiasse trasverso
b = semiasse non traverso
c2 = a2 + b2
Le coordinate dei fuochi sono:
F1(c,0) F2(-c,0)
Caratteristiche dell’iperbole
 L’equazione
x2 – y2 = 1
a2 b2
rappresenta un’iperbole riferita al centro e agli assi.
I punti in cui l’iperbole interseca gli assi coordinati sono detti vertici dell’iperbole.
Le coordinate dei vertici sono (+a,0). La curva è formata di due rami.
Osservando ancora la rappresentazione
grafica dell’iperbole, si vede che conducendo
le parallele all’asse y passanti per i vertici
e le rette parallele all’asse x passante per
i punti dell’asse y di ordinata b e –b
si ottiene un rettangolo: l’iperbole
è tutta all’esterno di tale rettangolo.
Asintoti

Le rette cui appartengono le
diagonali di tale rettangolo sono
dette asintoti dell’iperbole.
Le loro equazioni sono:
y=bx
a
e
y=-bx
a
I rami dell’iperbole si avvicinano ai propri asintoti a
mano a mano che il generico punto della curva si
allontana dall’origine.
Eccentricità

Il rapporto e = c/a viene detto eccentricità
dell’iperbole. E’ sempre maggiore di 1 e dà la misura
di quanto l’iperbole è aperta.
Le iperboli in figura (aventi lo
stesso fuoco) hanno
eccentricità diverse: 4, 2.81,
2.17, 1.76, 1.49, 1.28, 1.13,
1.01.
Iperbole equilatera

Se a = b l’iperbole si dice equilatera.
L’equazione è :
x2 – y2 = a2

In tal caso gli asintoti diventano:
y=x
y=-x
Se ruotiamo l’iperbole di 45° in
senso orario o antiorario, gli
asintoti vengono a coincidere
con gli assi cartesiani e
l’iperbole è ora riferita ai propri
asintoti. La sua equazione
diventa
xy = k
con |k| = a2 /2
k>0
L’iperbole in generale

L’iperbole si può trovare in posizioni diverse rispetto agli assi cioè avere
un qualsiasi punto del piano come centro di simmetria e rette diverse
dagli assi coordinati come assi di simmetria. L’equazione dell’iperbole
diventa:
ax2 + bxy + cy2 + dx + ey + f = 0
con Δ = b2 – 4ac > 0

Con opportune rotazioni e traslazioni
l’equazione dell’iperbole può essere
ricondotta alla forma normale.
Rappresentazione grafica di una
iperbole e del suo asintoto
Testo dell’esercizio da risolvere utilizzando il Programma Excel:
Rappresentare graficamente
l’iperbole y = 2x + 30/x
e
l’asintoto y = 2x
Fase di realizzazione 1:
 Creare
una nuova cartella di lavoro
All’interno di un foglio di lavoro si deve
creare una tabella con tre colonne non
attigue,
nella
prima
colonna
indicheremo i valori delle x, compresi
nell’intervallo -10 e 10 e con un passo
1. Nelle altre due colonne calcoleremo
con le formule i corrispondenti valori
della y appartenenti alla parabola e
all’asintoto
Fase di realizzazione 2:

Inserire il testo
Fase di realizzazione 3:

Inserire le formule
Cella
Valore da inserire
Risultato
A4
-10
-10
A5
=A4+1
-9
C4
=2*A4+30/A4
-23
E4
=2*A4
-20
Fase di realizzazione 4:

Copiare la formula della cella A5 nella zona
A6:A24
 Copiare la formula della cella C4 nella zona
C5:C24
Copiare la formula della cella E4 nella zona
E5:E24
Aspetto del foglio di lavoro:
Fase di realizzazione 5:

Eliminare la formula presente nella cella
C14 perché non si può effettuare una
divisione per zero, infatti Excel visualizza il
messaggio d’errore “#DIV/0!” e se si
lasciasse
questo
valore
la
rappresentazione
grafica
risulterebbe
errata
Fase di realizzazione 6:
Costruire il grafico
Per costruire il grafico in Excel devi selezionare la
zona contenente i dati utilizzando il tasto CTRL
dato che le zone non sono adiacenti. Selezionare
il pulsante Autocomposizione Grafico. Selezionare
il tipo di grafico “Dispers.(XY)”, e di questo tipo la
terza scelta “Dispersione con coordinate unite da
linee smussate e senza indicatori di dati”. Inserire
un titolo. Nell’ultima finestra di dialogo denominata
Posizione Grafico selezionare l’opzione “Come
Oggetto in” e infine il pulsante “Fine”
Aspetto del grafico:
Conclusioni:
Il foglio di lavoro che abbiamo predisposto può essere utilizzato per
la risoluzione dello stesso tipo di esercizio quante volte si vuole.
Infatti basterà modificare il titolo e le formule nelle celle C4 ed E4,
ricopiare le formule modificate nelle zone previste ed
automaticamente il grafico verrà aggiornato in base ai nuovi valori.
In questo modo si sfrutta una delle potenzialità di Excel che consiste
nell’aggiornamento automatico dei risultati al modificarsi dei dati di
origine.
In altre parole, se io predispongo un foglio di lavoro per la risoluzione
di un tipo di problema, al modificarsi dei dati di origine Excel mi
visualizza sempre il risultato corretto.