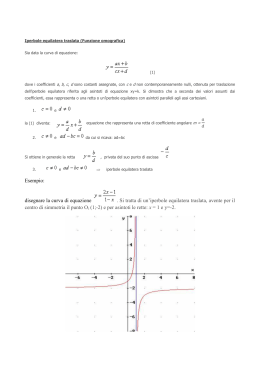
L’iperbole: problemi ed
equazioni
1
Bruna Cavallaro, Treccani Scuola
Tutto quello che sappiamo sull’equazione cartesiana
dell’iperbole con centro O e fuochi sull’asse x
Asintoti
c>a
a, b, c sono legati dal
teorema di Pitagora:
a2 = b2 + c2
c
Eccentricità e =
a
EQUAZIONE
x 2 y2
" 2 =1
2
a b
!
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
!
2
Elementi di simmetria dell’iperbole con centro O e
fuochi sull’asse x
EQUAZIONE
x 2 y2
" 2 =1
2
a b
!
A, A’ vertici dell’iperbole
L’equazione rimane inalterata se:
- cambio segno all’ascissa x;
- cambio segno all’ordinata y;
- cambio segno ad x e ad y.
Perciò l’iperbole è simmetrica
rispetto:
- all’asse y;
- all’asse x;
- all’origine O.
Che cosa succede se opero una simmetria rispetto alla bisettrice
del I e III quadrante, cioè se scambio x con y?
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
3
Equazione di iperbole con centro O e fuochi sull’asse y
Scambio x con y ed ecco che cosa ottengo.
c>a
EQUAZIONE
a, b, c sono legati dal
teorema di Pitagora:
c2 = a2 + b2
y2 x 2
" 2 =1
2
a b
c
Eccentricità e =
a
!
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
A, A’ vertici dell’iperbole
!
4
Attività 2. Equazione e grafico dell’iperbole
1%&2"*33/4%&%5(/67&8/&9"#22*&3%"7&8-8/.%6%&%&"/3*)(-"-&
2"*:)-4/&3#&-;#%</*$-&-&9"%=.*&8-))>/2-":*)-?&
@/(/8-6-(/&/$&9"#22/&8/&A&B&C&2-"3*$-D&%8&*9$/&9"#22*&
(/-$-&8%6%&#$%&3.E-8%&8/&)%(*"*&8%&.*42)-6%"-?&
!"#$#%&'%()*+,%-)%$#(./0%%
5
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
Che cosa abbiamo trovato
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
6
Riconoscere equazioni di iperbole con fuochi,
eccentricità ed asintoti
Una simmetria rispetto alla bisettrice del I e III quadrante scambia le
ascisse con le ordinate e trasforma la curva C nella D.
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
7
Risolvere problemi
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
8
Risolvere problemi
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
9
Risolvere problemi
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
10
Come sono stati realizzati i grafici di
iperbole di questa presentazione?
Con un software di geometria dinamica
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
11
Equazione e grafico di iperbole con un software
di geometria dinamica
Animazione ‘Iperbole_Geogebra_Presenta2’
Bruna Cavallaro, Treccani Scuola
12
Disegnare un’iperbole di equazione data
con un software di geometria dinamica
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
13
Iperbole: una curva tante equazioni
In questa lezione abbiamo ritrovato da un altro punto di
vista l’equazione dell’iperbole: è proprio la stessa curva
ottenuta alla fine di un lungo percorso che è cominciato
alla scuola secondaria con lo studio della
proporzionalità inversa.
Ecco una mappa sintetica del percorso.
Bruna Cavallaro, Treccani Scuola
14
L’iperbole: una curva, tante equazioni
Bruna Cavallaro, Treccani Scuola
15
Rivediamo alcune tappe del
percorso
Bruna Cavallaro, Treccani Scuola
16
Proporzionalità inversa e grafico di un ramo di iperbole
Rettangoli equivalenti
Capillarità
PROPORZIONALITÀ INVERSA
x, y lati di rettangoli di area 16
PROPORZIONALITÀ INVERSA
y altezza del liquido, x
diametro del capillare
Bruna Cavallaro, Treccani Scuola
17
Funzioni e grafico di un’iperbole
PROPORZIONALITÀ INVERSA
x, y lati di rettangoli di area 16
Legge: y = 16/x
Dominio: l’insieme R0+
Codominio: l’insieme R0+
Bruna Cavallaro, Treccani Scuola
GEOMETRIA ANALITICA
Iperbole
Equazione: y = 16/x
Campo di esistenza della
formula: l’insieme R0 dei
numeri reali diversi da 0
18
Simmetrie e grafico di funzioni del tipo y = k/x
Con la simmetria rispetto ad O trovo che una funzione del tipo y = k/x
ha per grafico un’iperbole con le caratteristiche indicate qui sotto.
k
y=
x
con k > 0
IPERBOLE EQUILATERA
RIFERITA AGLI ASINTOTI
A’ e B’ simmetrici di
A e B rispetto ad O
!
Bruna Cavallaro, Treccani Scuola
19
Rotazioni attorno ad O e iperbole equilatera
IPERBOLE EQUILATERA RIFERITA
AGLI ASSI DI SIMMETRIA
La curva è simmetrica rispetto a:
- asse delle x;
- asse delle y;
- origine O.
AA’ asse trasverso
A(a, 0) A’(!a, 0)
Vertici
Equazione
x2 ! y2 = a2
Bruna Cavallaro, Treccani Scuola
Asintoti d’equazione
y = x , y = !x
20
Trasformare un’iperbole con una dilatazione
Iperbole equilatera con:
- centro di simmetria O(0; 0);
- assi di simmetria gli assi cartesiani;
- asintoti y = x e y = -x;
- equazione x2 - y2 = 1.
Dilato il
piano Oxy
Iperbole che non è più equilatera,
ma ha sempre centro O(0; 0) e gli assi
cartesiani come assi di simmetria.
E l’equazione dell’iperbole e dei suoi asintoti?
Bruna Cavallaro, Treccani Scuola
21
Equazione dell’iperbole dopo la dilatazione
Bruna Cavallaro, Treccani Scuola
22
L’equazione di un’iperbole riferita agli assi di simmetria
‘Dimentico’ la dilatazione eseguita e gli apici nelle lettere
per concludere che:
2
2
Un’equazione del tipo x " y = 1
a2 b2
descrive un’iperbole con le caratteristiche indicate qui sotto.
Asintoti
!
Assi di simmetria
gli assi cartesiani
Centro O
Vertici A(a, 0) e A’(-a,0)
AA’ asse trasverso
Daniela Valenti, Treccani Scuola
23
Equazione dell’iperbole come luogo di punti
Bruna Cavallaro, Treccani Scuola
24
Tutto quello che sappiamo sull’equazione cartesiana
dell’iperbole con centro O e fuochi sull’asse x
Asintoti
c>a
a, b, c sono legati dal
teorema di Pitagora:
a2 = b2 + c2
c
Eccentricità e =
a
EQUAZIONE
x 2 y2
" 2 =1
2
a b
!
!"#$%&'%(%))%"*+&,"-..%$/&0.#*)%&
!
25
Iperbole nella realtà e nelle scienze
L’iperbole è una curva molto ricca di proprietà, studiate
già dagli antichi greci e perciò è diventata sempre più
importante nella realtà e nelle scienze.
Bruna Cavallaro, Treccani Scuola
26