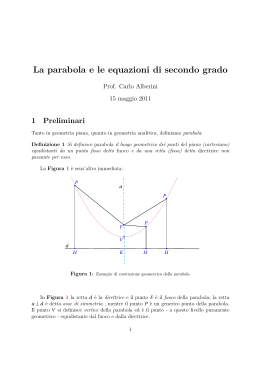
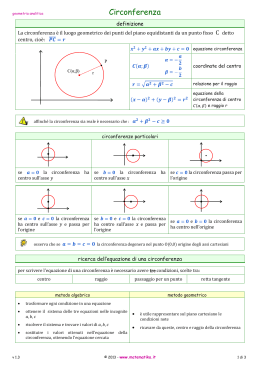
Problemi risolvibili con la regola
di Cardano
Le equazioni di terzo grado in cui manca il termine di
secondo grado(z3=± pz+q) possono essere risolte
mediante una particolare regola, la regola di Cardano.
Queste equazioni possono essere risolte anche
supponendo un cerchio NQPV i cui archi NQP e NVP sono
divisi in tre parti uguali.
La somma di NQ, cioè la corda
sottesa alla terza parte di NQP,
e NV, cioè la corda sottesa alla
terza parte di NVP, corrisponde
alla radice dell’equazione.
Questo metodo può essere
utilizzato per risolvere anche
le equazioni che vanno fino al
quadrato del quadrato.
Problemi solidi
1.
2.
I problemi solidi non possono essere costruiti senza
che si utilizzi qualche linea più composta della
circonferenza.
Questi sono riducibili a due costruzioni:
Una in cui si richiedono insieme i due punti che
determinano due medie proporzionali tra due linee
date;
Un’altra in cui si richiedono i due punti che dividono in
tre parti uguali un arco dato.
Le curvature delle coniche, dato che dipendono
sempre da due elementi diversi, possono servire anche
a determinare due differenti punti.
Per questa ragione è impossibile che problemi che sono
di un grado più composti di quelli solidi e che
presuppongono di trovare quattro medie proporzionali o
la divisione di un angolo in cinque parti uguali possono
essere costruiti utilizzando queste coniche.
Per costruire, quindi, tali problemi bisogna utilizzare la
curva che si descrive mediante l’intersezione di una
parabola con una retta.
Problemi ridotti ad un’equazione
di sesto grado
Alcuni problemi possono essere risolti
riconducendoli all’equazione:
y6-py5+qy4-ry3+syy-ty+u=0
in cui la quantità q sia maggiore del
quadrato della metà di quella p.
Dal grafico si può vedere che la parabola
con la circonferenza si intersecano in tanti
punti quante sono le radici dell’ equazione.
In questo modo le perpendicolari condotte
da tali punti sulla retta, come CG, NR, QO,
saranno le radici cercate.
Medie proporzionali
Se vogliamo trovare quattro medie
proporzionali tra le linee a e b, cioè
quattro segmenti x,y,z,k, posto x per la
prima abbiamo:
a:x = x:y = y:z = z:k = k:b
Risolvendo queste proporzioni si otterrà:
x5-a4b=0
Come si può notare dal disegno la circonferenza taglia la
parabola nei due punti C ed N: da questi punti si
conducono le perpendicolare NR e CG, togliendo poi
dalla maggiore CG la minore NR, il resto sarà x, cioè la
prima delle quattro medie proporzionali cercate.