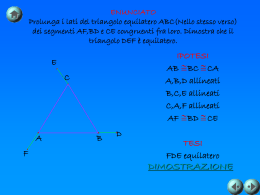
IL TEOREMA DEL
TRIANGOLO ISOSCELE
(Prof. Daniele Baldissin)
Euclide, Libro 1 - Proposizione 5
In epoca medievale, quando la geometria rappresentava
uno dei quattro soggetti del Quadrivium, questo teorema
assunse la reputazione di una difficile prova per un
principiante, chi non avesse la padronanza della sua
dimostrazione non sarebbe stato in grado di procedere con
degli studi più avanzati. Forse per questo il teorema divenne
noto come il pons asinorum o ponte degli asini. Questo
termine è usato come metafora per una prova che permetta
una selezione tra chi è più dotato in una materia e chi meno.
PROPOSIZIONE
Se un triangolo è isoscele allora gli angoli alla base sono
congruenti.
Dimostrazione
Si considerino i triangoli ABD e ACE:
per ipotesi
I due triangoli sono congruenti per il
primo criterio di congruenza e, di conseguenza BD è congruente a CE
Si considerino i triangoli BDC e BCE.
Si ha che:
BC è in comune ai due triangoli
perchè dimostrato prima
b
g
I due triangoli sono congruenti per il
∧
terzo criterio di congruenza e, di conseguenza l’angolo EBC è congruente
∧
all’angolo BCD. I loro supplementari b e g (angoli alla base) saranno di conseguenza
congruenti.
C.V.D.