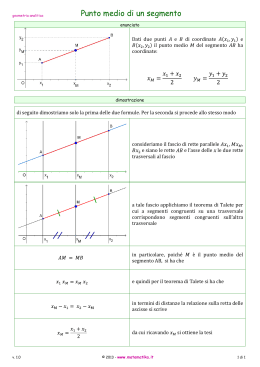
ITCG Mosè Bianchi
Autore: Beretta Andrea
Classe A2 Geometri
Dato un fascio di rette parallele,
tagliato da due trasversali a
segmenti congruenti sull’una
corrispondono segmenti
congruenti sull’altro
Un fascio di rette parallele...
r
...è tagliato da due trasversali.
a
A
b
B
c
d
C
D
r’
A’
B’
C’
D’
IPOTESI:
TESI:
ABCD
A’B’C’D’
a//b//c//d
r
a
A
A’
b
B’
B
c
d
r’
E
C’
C
D’
D
F
Dobbiamo dimostrare che A’B’C’D’ sapendo che ABCD
Conduciamo da A
e C le parallele
AE,CF alla retta r’
che risultano
perciò parallele fra
loro (per teorema)
r
a
r’
A’
A
b
B
c
d
E
B’
C’
C
D’
D
F
r
Consideriamo i
triangoli ABE e CDF.
a
r’
A’
A
b
Essi hanno
c
•AB  CD per ipotesi
• BAˆ E  DCˆ F perché angoli d
corrispondenti formati dalle
parallele AE e CF tagliate da r
ˆ F perché angoli
• ABˆ E  CD
corrispondenti formati dalle
rette parallele b,d tagliate da r
B
E
B’
C’
C
D’
D
F
r
Consegue che
i triangoli
ABE e CDF
sono
congruenti
per il secondo
criterio di
congruenza
dei triangoli
a
r’
A’
A
b
B
c
d
E
B’
C’
C
D’
D
F
Dall’uguaglianza dei due triangoli si deduce che:
AE  CF
ma AE  A’B’ e CF  C’D’
perché segmenti
paralleli compresi
fra rette parallele,
perciò, per la
proprietà transitiva
della congruenza,
A’B’ C’D’
Come volevasi
dimostrare
r
a
r’
A’
A
b
B
c
d
E
B’
C’
C
D’
D
F