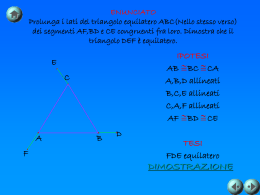
Europa 2013
QUESITO 1
Dato un triangolo ABC, si indichi con M il punto medio del lato BC. Si dimostri che
la mediana AM è il luogo geometrico dei punti P del triangolo, tali che i triangoli ABP e ACP
hanno aree uguali.
Sia P un punto della mediana AM.
Si deve dimostrare che i triangoli ABP e ACP hanno aree uguali
Se P
la tesi è dimostrata in quanto i triangoli sono entrambi degeneri e
hanno area nulla
Se P
ABM e ACM hanno aree uguali avendo in comune l’altezza ( il
segmento AH) e le basi BM e CM tra loro congruenti.
Se P è interno al segmento AM i triangoli MBP e CMP hanno aree uguali
avendo in comune l’altezza ( il segmento PK) e le basi BM e CM tra loro congruenti.
Allora le aree dei due triangoli ABP e ACP sono uguali perché differenza di aree uguali.
Viceversa
Sia P un punto interno al triangolo tale che i triangoli ABP e ACP abbiano aree uguali , si deve
dimostrare che P appartiene ad AM
Essendo comune la base AP, le due altezze BJ e CI sono necessariamente
congruenti.
Prolungando la semiretta AP fino ad incontrare in M’ il segmento BC, si
osserva che anche i due triangoli ABM’ e ACM’, hanno uguale area , avendo
in comune la base AM’e le altezze BJ e CI tra loro congruenti
Per quanto dimostrato prima , M’ deve coincidere con M e, di conseguenza
Soluzione di Adriana Lanza