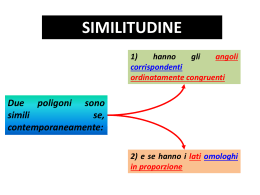
Trasformazioni non isometriche
LA SIMILITUDINE
Vi sono coppie di figure simili?
Quando due figure sono simili
IN MATEMATICA?
C
B
D
G
F
A
H
- GLI ANGOLI CORRISPONDENTI
CONGRUENTI
- I LATI CORRISPONDENTI
PROPORZIONALI:
il rapporto costante è
la COSTANTE DI SIMILITUDINE
E
AB BC CD DA
k



EF FG GH HE
ESEMPIO
I triangoli
NON SONO SIMILI
nonsono
hanno simili?
i lati in proporzione.
I triangoli
ABC perché
e DEF
C
D
6
F
13
12
5
A
10
B
7
E
ABC è simile a DEF se i lati corrispondenti sono in proporzione.
10 ? 12 ? 13


5
6
7
2 sì 2 no 13


1
1
7
ESEMPIO
I trapezi sono simili: calcola la misura del lato FG
.
C
G
B
6
x
D
2
A
H
2 6

4 x
2:4  6: x
46
x
 12
2
4
E
F
ESEMPIO
I triangoli isosceli sono simili:
calcola la misura dell’angolo A
.
F
C
30°
30°
x
A
Â @ D̂
B
D
D̂ = (180°-30°) : 2 = 150° : 2 = 75°
Â = 75°
E
Proprietà di figure simili
 Il rapporto tra i perimetri
è uguale alla costante
di similitudine.
 Il rapporto tra le aree è
uguale al quadrato
della costante di
similitudine.
2 p'
2p
A'
A
2p
k
2 p'
A
 k2
A'
Criteri di similitudine dei
triangoli
PER I TRIANGOLI ESISTONO DELLE
PROPRIETÀ CHE TI PERMETTONO DI
STABILIRE SE DUE TRIANGOLI SONO SIMILI:
LE PROPRIETÀ SONO TRE E VENGONO DETTE
CRITERI DI SIMILITUDINE.
1° Criterio di
similitudine
Due triangoli
sono simili se
hanno gli
angoli
ordinatamente
congruenti.
10º
50º
120º
120º
10º
50º
5
9 1


15 27 3
2° Criterio di
similitudine
Due triangoli
sono simili se
hanno un
angolo
congruente e i
lati che lo
delimitano in
rapporto
costante.
5
50º
9
15
50º
27
5
3° Criterio di
similitudine
Due triangoli
sono simili se
hanno i lati in
rapporto
costante.
4
6
15
12
18
5
6
4 1



15 18 12 3