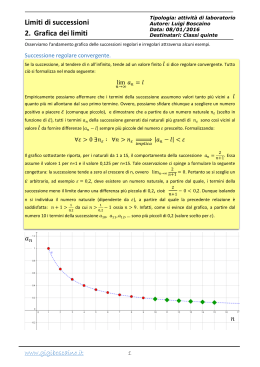
Successioni
Chiamiamo successione una funzione f : ℵ0 → ℜ che associa ad ogni numero naturale
diverso da zero un numero reale.
1
a1
2
3
a3
a2
Ad esempio la funzione matematica definita dalla legge: f (n) = n 2 + 1 origina la
successione che ha come elementi i numeri: 2; 5; 10; …………..
Limiti di successioni convergenti
•
Diciamo che la successione a1 , a 2 , ....., a n ha limite l per n → +∞ , quando, scelto ad
arbitrio un numero positivo ε , è possibile determinare in corrispondenza ad esso un
numero nε tale che ∀ n > nε sia verificata la disuguaglianza: a n − l < ε , ossia:
l − ε < a n < l + ε e scriveremo:. lim a n = l (1)
n → +∞
In tal caso diremo che la successione è convergente.
Esempio 1
n +1
= 1 equivale a dimostrare che esistono dei valori di n per i quali è
n → +∞ n
n +1
1
soddisfatta la disequazione:
− 1 < ε ⇒ < ε (2)
n
n
1
1 1
1
1
Poiché n > 0 ⇒
> 0 e che
= , la (2) può essere scritta < ε ⇔ n > .
n
n n
n
ε
1
Ponendo nε = abbiamo verificato che esistono elementi della successione aventi indice
Verificare che lim
ε
n > nε
che verificano la disequazione
n +1
= 1.
n → +∞ n
lim
n +1
− 1 < ε .Possiamo quindi affermare che:
n
Per meglio capire la definizione di limite supponiamo di aver scelto ε =
Poiché
1
ε
1
.
10
= 10 , scegliamo il dodicesimo termine (n>10) della successione a12 =
osserviamo che 1 −
1 13
1
<
< 1+
10 12
10
⇔
13
e
12
9 13 11
<
<
⇔ 0,9 < 1,08 < 1,1.
10 12 10
Esempio 2
3n 2
= 3 (1)
n → +∞ n 2 + 1
3n 2
−3
equivale a dimostrare che 2
< ε. ⇔
− 3 < ε . Osserviamo che: 2
n +1
n +1
Verificare che lim
questa ha come soluzioni: n < −
3
ε
−1 e n >
3
ε
− 1 . (con
3
ε
− 1 > 0 ).
Poiché la prima disuguaglianza è impossibile, deve essere n >
Ponendo nε =
3
ε
3
<ε e
n +1
2
3
ε
−1 .
− 1 ∃ n > nε per i quali vale la (1).
Se ε = 0,1 per n > nε = 29 , scegliamo il sesto termine della successione a 6 =
verifichiamo che: 2,90 < 2,91 < 3,1 .
39
e
37
Limiti di successioni divergenti
• Diciamo che la successione a1 , a 2 , ....., a n ha limite + ∞ per n → +∞ , quando, scelto
ad arbitrio un numero M>0, grande a piacere, è possibile determinare in
corrispondenza ad esso un numero nM tale che per ogni n> nM si ha an > M.
Si dice in tal caso che la successione è positivamente divergente e si scrive
lim a n = +∞ .
n → +∞
Esempio 3
n2 +1
= +∞
n → +∞
n
Verificare che lim
(1)
n2 +1
> M (2).
n
Poiché n>0 consideriamo solamente n 2 − Mn + 1 > 0 (con ∆ = M 2 − 4 > 0) .
Equivale a dimostrare che esistono elementi della successione per cui
Osserviamo che la (2) è verificata per n <
M− ∆
M+ ∆
∨ n>
.
2
2
M + M2 −4
la (1) è verificata ∀ n > n M .
2
10000 + 1
> 100.
Infatti se M=100 si ha: nM=99,98 e, per n=100
100
Posto: n M =
•
Diciamo che la successione a1 , a 2 , ....., a n ha limite − ∞ per n → +∞ , quando, scelto
ad arbitrio un numero M>0, grande a piacere, è possibile determinare in
corrispondenza ad esso un numero nM tale che per ogni n> nM si ha an < -M.
Si dice in tal caso che la successione è negativamente divergente e si scrive
lim a n = −∞ .
n → +∞
Verificare che lim (n − 2n 2 ) = −∞
n → +∞
equivale a dimostrare che esistono elementi della successione per cui: n − n 2 < − M (2).
1 + 1 + 8M
Risolvendo si ha: n >
= n M . Per M=100 ed nM=30 risulta (30-1800)< -100.
4
NOTA
Esistono successioni che non ammettono né limite finito né limite infinito e non sono né
convergenti né divergenti. Esse si dicono
indeterminate. Ad es. an=(-1)n.
Il numero e
n
 1
lim 1 +  = e
n → +∞
 n
Sviluppando la potenza del binomio mediante la formula di Newton otteniamo:
n
0
n 0 1
 n  n −0  1   n  1  n  1
 1
1 +  =   1   +   1 +   1 2 + ......... +   1 n =
 n  1  n  2  n
 n
n n
0
= 1+ n
1 n(n − 1) 1
1
+
+ ............... + n .
2
n
2! n
n
Essendo vera l'uguaglianza:
1
1 n −1 n − 2
n − (n − 1)
= ⋅
⋅
⋅ ............. ⋅
=
n
n! n
n
n
n
=
1  1  2
 n −1
⋅ 1 −  ⋅ 1 −  ⋅ ............ ⋅ 1 −
 si ha:
n!  n   n 
n 

n
1  1  1  1  2 
1  1  2
 1
 n −1
1 +  = 1 + 1 + 1 −  + 1 − 1 −  + ........... + ⋅ 1 −  ⋅ 1 −  ⋅ .... ⋅ 1 −
.
2 !  n  3!  n  n 
n!  n   n 
n 
 n

All'aumentare di n il secondo membro dell'uguaglianza cresce perché cresce il numero dei
termini che sono tutti positivi. La successione è crescente e quindi esiste il limite per n che
tende a + ∞ .
Poiché le quantità tra parentesi sono tutte minori di 1 ed essendo
1 1 1
1
1
1
< ; < 2 ; ....; < n −1 possiamo scrivere:
2! 2 3! 2
n! n
n
1 
 1
 1 1
1 +  < 1 + 1 + + 2 + ......... + n −1  .
n 
 n
 2 2
Osservando che la quantità tra parentesi è la somma dei primi n termini di una
1
1− qn
progressione geometrica di ragione q = e ricordando che S n = a1
si ha:
2
1− q
n
1
1−  
n
1 
1 
2
 1



= 21 − n  Quindi 2 < 1 +  < 1 + 21 − n  < 3.
Sn =
1
 2 
 n
 2 
1−
2
La successione data ha per limite un numero compreso tra 2 e 3. Detto numero è
irrazionale ed è la base dei logaritmi naturali o neperiani. Il suo valore è 2,71828…..
Ad Eulero è dovuta la dimostrazione della sua irrazionalità.