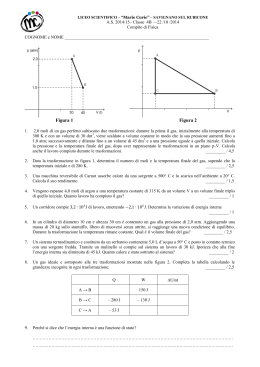
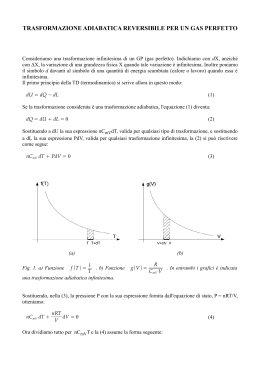
Esercizio n.21 di pagina 98.
m = 90 g
tA = 10 °C
tB = 100 °C
pa = 1.013105 Pa
massa di azoto N2 (gas biatomico)
temperatura iniziale nello stato termodinamico A
temperatura finale nello stato termodinamico B
pressione atmosferica (costante)
calcoliamo dapprima le temperature assolute:
Determiniamo la variazione di energia interna U e il lavoro L con le seguenti relazioni:
(si noti il valore 5 invece del valore 3 tipico dei gas monoatomici)
Per entrambe è necessario determinare il numero di moli partendo dalla massa e dalla massa molecolare
Otteniamo quindi:
Per il calcolo di Q ricorriamo all’equazione della prima legge della termodinamica:
Per esercizio si può determinare Q applicando l’equazione fondamentale della calorimetria espressa in
funzione del numero di moli e del calore specifico molare a pressione costante:
Esercizio n.23 di pagina 98.
n = 2 moli
 = 1.40
L=?
U = ?
Q=?
quantità di gas ideale (espressa in moli) sottoposta al processo ABC
rapporto tra Cp e Cv del gas
lavoro totale compiuto durante il processo
variazione di energia interna
calore totale scambiato durante il processo
Le due trasformazioni cui è sottoposto il gas A Y B e B Y C non sono catalogabili tra quelle tipiche (isocora;
isobara; isotermica; adiabatica) per cui non possiamo utilizzare nessuna delle relazioni conosciute; possiamo
però considerare che il lavoro compiuto o subito dal sistema durante una trasformazione termodinamica è
uguale all'area sottesa al cammino della trasformazione nel diagramma P-V (piano di Clapeyron). L'area
sottesa ai segmenti AB e BC è scomponibile in un triangolo e un rettangolo, per cui si ha:
La variazione di energia interna complessiva dipende solo dalle temperature nello stato finale C e nello
stato iniziale A.
K è ricavabile dall'espressione
poiché  = 1.4 ricaviamo K= 5. (cfr. pag.77 del libro di testo)
La variazione di temperatura si determina scrivendo l'equazione di stato dei gas perfetti per lo stato A e per
lo stato C, sottraendo membro a membro quella in C da quella in A, ed ottenendo:
Sostituendo quest'ultima nella (1) si ha
Per il calcolo di Q ricorriamo all’equazione della prima legge della termodinamica:
Relativamente al segno, L, U e Q sono tutti e tre positivi. Il lavoro, in una trasformazione in cui vi è
aumento di volume, è positivo (si noti il verso di percorrenza della serie di trasformazioni). La variazione di
energia interna è positiva in quanto vi è un aumento di temperatura.
Esercizio n.26 di pagina 98.
V0 = 16000 cm3
n = 1.1 moli
t0 = 30 °C
V1 = 1600 cm3
t1 = ?
L=?
volume occupato dal gas prima della compressione
quantità di gas CO2 sottoposta a compressione adiabatica
temperatura iniziale del gas
volume occupato dal gas dopo la compressione
temperatura del gas dopo la compressione
lavoro compiuto sul gas
In una trasformazione adiabatica si hanno le seguenti relazioni tra pressione e volume e tra temperatura
assoluta e volume:
Dalla (2) determiniamo T1 dopo aver calcolato T0 in kelvin:
In cui  = 1.3 (tabella 3.1 pagina 77)
Dalla relazione della prima legge della termodinamica, considerando che non vi è scambio di calore con
l'ambiente essendo la trasformazione adiabatica, la quantità di calore è zero:
Considerando che il gas è poliatomico K assume il valore 7, e quindi: