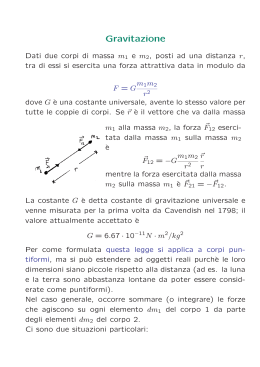
Forza gravitazionale
Terra
Pianeti interni
Marte
Mercurio
Venere
Plutone
Urano
Nettuno
Giove
Saturno
Sistema solare
Il moto dei pianeti descritto dalle 3 leggi di Keplero
Di qui Newton ricavò la legge di gravitazione universale: 1a forza fondamentale
1a Legge di Keplero
i pianeti si muovono su orbite piane ed ellittiche, aventi il sole in uno dei fuochi
se si estende al moto di un corpo qualsiasi, la condizione
è che sia una conica (ellisse, iperbole o parabola)
a
2a Legge di Keplero
la velocità areolare è costante
5,5
5,0
Legge di Keplero
Il quadrato del tempo di rivoluzione è
proporzionale al cubo del semiasse maggiore
Verifica con dati presi da internet:
T ∝a
2
3
log T = 1.5 log a + k
Solo se (Msole >> Mpianeta)
y = 1,4999x + 2,5626
4,5
4,0
log(T(d))
3a
3,5
3,0
2,5
2,0
1,5
-0,5
0
0,5
log(a (AU))
1
1,5
2
Legge di Gravitazione Universale
m1 m 2
F =G
r2
G = 6.6742.10-11 m3/(kg s2)
♦ Forza sempre attrattiva
La costante G è “piccola”.
♦ Interazione fra 2 corpi + principio di sovrapposizione.
♦ Rigorosamente vera per corpi puntiformi ma …
♦ … anche per corpi sferici se si considera la distanza dal centro
M
m
m
manubrio mobile
M
Misurata in laboratorio da Cavendish
nel 1798 con bilancia a torsione
Gravitazione in prossimità della superficie terrestre
La forza peso è la forza di attrazione gravitazionale da parte della Terra.
Se ne deducono alcune proprietà come la dipendenza di g dall’altezza.
Nota g e la legge di gravitazione universale si può ricavare la massa terrestre.
mg
mT
R
mg = G
m
mT m
R2
gR 2
⇒ mT =
= 5.97 ⋅10 24 kg
G
essendo R = 6371 km il raggio medio terrestre
Come varia g con l’altezza?
GmT
g (h ) =
(R + h )2
2
GmT
GmT  R 
 R 
g (h ) =
=
=
g
(
0
)




(R + h )2 R 2  R + h 
 R+h
h=32km per riduzione dell’1%
2
Gravitazione in prossimità della superficie terrestre
perché l’accelerazione “di gravità” non è costante sulla superficie terrestre?
1. Rotazione
quanto varia N all’equatore, per la rotazione terrestre?
r
mg
r
N
Che succede alle altre latitudini?
equatore
9,8065 m/s2 non è la «vera» accelerazione di gravità!
2. Deformazione
In prima approssimazione la terra è un ellissoide
di rotazione:
R EQ = 6378,137 km
R POL = 6356,752 km
la cui superficie è ortogonale a
r
g eff
accelerazione di gravità o campo gravitazionale?
agente su un corpo
La quantità
Forza gravitazionale
massa
si chiama anche Campo gravitazionale
del corpo
è la stessa cosa dell’accelerazione di gravità. Cambia però il modo di vedere
Due Teoremi
il campo gravitazionale generato da una distribuzione sferica di massa, all’esterno,
è uguale a quello che sarebbe generato dalla stessa massa, puntiforme, posta al centro
il campo gravitazionale generato da una distribuzione superficiale sferica di massa
(un guscio sferico), all’interno è nullo.
che succede all’interno della Terra?
Orbite circolari.
In generale le orbite dei pianeti sono ellittiche e seguono le leggi di Keplero.
Noi ci limiteremo ad orbite circolari (moto circolare uniforme).
Es. pianeta in orbita circolare intorno al sole.
v
mP
r
m m
v2
mP
= m Pω 2 r = G P 2 S
r
r
 4π 2  3
2
 r
T = 
3a legge di Keplero
 Gm S 
ecco la costante
di proporzionalità!
Nota G e i parametri dell’orbita terrestre,
o di altri pianeti, si ricava la massa del sole
mS = 1.99 ⋅1030 kg
Per un satellite in orbita intorno alla terra, a distanza r dal centro:
T
2
 4π 2
= 
 Gm T
 3
 r

Se l’orbita è geostazionaria:
T=24h => h = 35800 km
Lavoro della forza gravitazionale. Caso generale.
Se gli spostamenti sono grandi e non è lecito considerare costante l’accelerazione
di gravità. Bisogna utilizzare l’espressione generale che, per due corpi, vale:
FG = G
Anche in questo caso si trova che il lavoro non dipende dal percorso
in uno spostamento infinitesimo:
r
r1
F1
r
r2
dL = 0
r
r
dL = FG ⋅ d s ⇒
F2
dL = − G
m1 m 2
dr
2
r
quindi il lavoro è pari a:
1 1
L = Gm1m2  − 
 r2 r1 
O
m1m2
r2
Energia Potenziale Gravitazionale
A) Approssimazione di forza costante (es. in prossimità della superficie terrestre)
U B − U A = mgy B − mgy A
da cui si ricava
U = mgy
+ cost
dove y è la posizione lungo l’asse verticale orientato in su. Di solito si pone cost=0
(equivale a prendere U(y=0)=0: si assume un livello di riferimento y=0)
B) Caso generale (Legge di gravitazione di Newton)
Gm 1 m 2 Gm 1 m 2
U B −U A = −
+
rA
rB
da cui
U =−
Gm 1 m 2
r
+ cost.
di solito si pone cost = 0 (U nulla a distanza infinita)
Il secondo caso mette in evidenza che l’energia potenziale è l’energia potenziale del
sistema di due masse m1 e m2: ad esempio del sistema Terra + palla
Per corpi estesi ma sferici vale la stessa formula, dove r è la distanza fra i centri.
Energia potenziale gravitazionale
La forza di gravitazione universale è conservativa. L’energia potenziale è:
Gm 1 m 2
U =−
r
assumendo U=0 a distanza infinita
0
grafico dell’energia
EM
U
Applicazioni:
Stimare la velocità al suolo di un
meteorite (da grande distanza)
Calcolare la velocità di fuga dalla terra.
Forza gravitazionale. Conservazione dell’energia
Un oggetto è lanciato verso l’alto, dalla superficie terrestre,
con velocità v0. Calcolare l’altezza massima raggiunta
(trascurando la resistenza dell’aria)
In approssimazione di g costante si aveva:
Ma g varia con l’altezza!
m 2
v02
v0 = mgh ⇒ h =
2
2g
V0 (m/s)
h (g cost) (km)
h esatto (km)
∆h/h (%)
Usando l’espressione esatta:
1000
50,97
51,38
0,8
m 2 GMm
GMm
v0 −
=−
2
R
R+h
2000
203.9
210,6
3,2
5000
1274
1593
20
8000
3262
6682
51
per
h→∞
Mm m 2 
+ v 
R
2 ⇒ v =
E F = E PF + E KF = 0 
E I = −G
Velocità di fuga
2GM
R
Velocità minima affinché si un corpo
si allontani indefinitamente
per la Terra vF= 11180 m/s = 40250 km/h
Osservazioni
Mm
FG = G 2
r
è la stessa cosa, se si considera che
presso la superficie terrestre
g è praticamente costante:
GMm
U =−
r
?
FG = mg
o
o
M
g (r ) = G 2
r
r = R+h≅ R
U = mgy
M
g0 = G 2
R
?
l’espressione a destra vale solo nel limite di g costante, ovvero in una regione limitata
r = R+ y
con
y << R
GMm  GMm 
 GM 
≅ −
U =−
 + m 2  y
R+ y 
R 
 R 
U ≅ cost + mgy