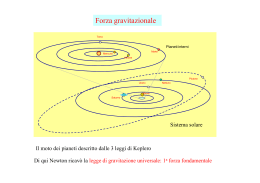
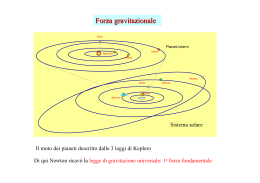
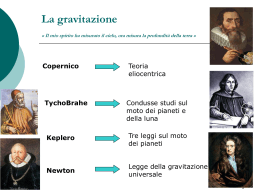
Legge di Gravitazione Universale e Leggi di Keplero Legge di gravitazione universale (Newton): →
Due masse puntiformi M ed m si attraggono sempre con una forza F il cui modulo è direttamente proporzionale alle masse stesse ed inversamente proporzionale al quadrato delle loro distanze: F =G
M ⋅m
d2
G è una costante universale detta costante di gravitazione universale ( il suo valore dipende dunque esclusivamente dalle unità di misura scelte). Nel S.I.: G = 6,67 ⋅ 10
−11
N ⋅ m2
Kg 2
⎡ F ⋅ d 2 ⎤ ⎡ m a l 2 ⎤ ⎡ l ⋅ t −2 ⋅ l 2 ⎤
−1 3 − 2
Equazione dimensionale di G: [G ] = ⎢
⎥=⎢
⎥=⎢
⎥= m l t ⎣ M ⋅ m ⎦ ⎣ m⋅ m ⎦ ⎣ m ⎦
[
]
Ricordando che in prossimità della Terra il peso P coincide con la forza gravitazionale applicata ad m quando M=MT e R=RT : P = mg , F = G
MT ⋅ m
RT2
ma
P=F
⇒
mg = G
MT ⋅ m
G ⋅ MT
⇒ g =
2
RT
RT2
Essendo MT=5.98∙1024Kg e RT=6,4∙106m → g=9,8m/s2 (come del resto era a noi noto). Massa gravitazionale e massa inerziale Distinguiamo due tipi di massa: •
•
Massa gravitazionale: è la proprietà che possiede una massa M di determinare una regione circostante dove una qualunque massa spia m risente di una forza di tipo gravitazionale. In altri termini è la proprietà che possiede la massa M di generare un campo gravitazionale. Massa inerziale: è una grandezza che misura l’attitudine che possiede la massa M a conservare il proprio stato d’inerzia (cioè di quiete o di moto). N.B.: pur essendo concettualmente diverse, le due masse in precedenza introdotte sono equivalenti per uno stesso corpo e cioè ammettono la stessa misura. E’ questo il motivo per cui generalmente si parla di massa senza specificare se ci si riferisca all’una o all’altra(cosa questa affidata al contesto). Leggi di Keplero 1° legge I pianeti, nel loro moto intorno al Sole, descrivono orbite ellittiche di cui i Sole stesso occupa uno dei fuochi. 2° legge Definito raggio vettore la congiungente un assegnato pianeta al Sole, il raggio vettore spazza (descrive) nel tempo una certa superficie. La seconda legge di Keplero afferma che le aree descritte dai raggi vettori sono direttamente proporzionali ai tempi impiegati a descriverli e dunque il rapporto S/Δt è costante. A Attraverso questa legge si possono determinare D informazioni circa la velocità dei pianeti. Se, con riferimento alla figura, S1=S2 allora S1 S 2 Δt1=Δt2 e dunque i due archi AB e CD vengono descritti nello stesso tempo e ciò implica che la C velocità v1 nel primo tratto è maggiore della B velocità v2 nel secondo tratto. Detti perielio il punto dell’orbita più vicino al Sole e afelio il punto dell’orbita più lontano dal Sole, da quanto detto segue che la velocità lineare lungo l’orbita ellittica è massima al perielio e minima all’afelio. 3° legge Indichiamo con T il periodo di rivoluzione di un pianeta, ovvero il tempo impiegato a descrivere l’intera orbita. la terza legge di Keplero mette in relazione la forma dell’ellisse con il tempo impiegato a descriverla. Essa afferma che: T2
= cos t. dove a è il semiasse maggiore dell’ellisse stessa. a3
In particolare ciò comporta che all’aumentare della distanza dei pianeti dal Sole, aumenta il loro periodo di rivoluzione. Qualche Test 1. Se MT è la massa terrestre, RT il raggio terrestre, G la costante di gravitazione universale, G MT
allora ci fornisce: RT2
A. La forza peso B. L’accelerazione centripeta C. La forza di gravitazione universale D. L’accelerazione di gravità g E. Nessuna delle risposte precedenti è esatta 2. Se la distanza tra due masse M e m raddoppia, allora: A. La forza gravitazionale raddoppia B. La forza gravitazionale si dimezza C. La forza gravitazionale aumenta di 4 volte D. La forza gravitazionale diminuisce di 4 volte E. La forza gravitazionale resta invariata 3. Relativamente al moto di un pianeta intorno al Sole: A. La velocità è la stessa in modulo sia all’afelio che al perielio B. La velocità è maggiore al perielio C. La velocità è maggiore all’afelio D. Il perielio è il punto di massima distanza dal Sole E. Il Sole occupa il centro dell’orbita 4. In base alla terza legge di Keplero: A. Il tempo di rivoluzione del pianeta è direttamente proporzionale al quadrato del semiasse maggiore dell’orbita B. Il quadrato del tempo di rivoluzione è direttamente proporzionale al cubo del semiasse maggiore dell’orbita C. Il cubo del tempo di rivoluzione è direttamente proporzionale al quadrato del semiasse maggiore dell’orbita D. Il tempo di rivoluzione è direttamente proporzionale al semiasse maggiore dell’orbita E. Non esiste alcuna proporzionalità tra il tempo di rivoluzione e il semiasse maggiore dell’orbita 5. Un corpo ha una certa massa M. Se viene portato sulla Luna, la sua massa: A. non varia B. diminuisce C. aumenta D. si annulla E. raddoppia 6. Il peso di un corpo: A. È una grandezza che dipende sia dalle caratteristiche del corpo che dalla sua posizione B. È una caratteristica del corpo che si può stabilire una volta per tutte C. È una grandezza che caratterizza un corpo solo se è in quiete D. Per la legge di gravitazione universale dipende quadraticamente dalla massa del corpo E. Quesito senza soluzione univoca o corretta 7. Un corpo sulla Terra ha una certa massa e un certo peso. Se esso fosse portato sulla Luna cosa cambierebbe? A. Il valore della massa B. Il valore del peso C. Cambierebbero entrambi ma non il loro rapporto D. Non cambierebbe alcuna grandezza E. Cambierebbe il prodotto della massa per il peso 8. Un satellite ruota intorno alla Terra su un’orbita circolare. Se il raggio dell’orbita viene fatto triplicare, la forza con la quale la Terra attrae il satellite: A. Rimane invariata B. Diminuisce di tre volte C. Dipende dalla massa del satellite D. Diminuisce di nove volte E. Aumenta di nove volte 9. L’accelerazione di gravità sulla Luna è circa 1/6 di quella sulla Terra. La massa di un uomo che si trova sulla Luna è: A. 1/6 di quella che ha sulla Terra B. 6 volte quella che ha sulla Terra C. Uguale a quella che ha sulla Terra D. 1/36 di quella che ha sulla Terra E. 1/9,8 volte quella che ha sulla Terra 10. Il peso di un corpo sulla Luna è minore del peso dello stesso corpo sulla Terra perché: A. La Luna è priva di atmosfera B. Il raggio della Luna è minore della massa della Terra C. La massa della Luna è minore della massa della Terra D. Il rapporto tra la massa e il quadrato del raggio è minore per la Luna che per la Terra E. La massa del corpo è minore sulla Luna 11. Le forze di attrazione Terra – Luna e Luna – Terra: A. Sono uguali in modulo ma opposte B. Sono uguali in modulo, direzione e verso C. La prima è maggiore della seconda D. La seconda è maggiore della prima E. Quesito senza soluzione univoca o corretta 12. La legge di gravitazione universale vale: A. Solo per masse puntiformi B. Solo per sistemi Terra – Sole C. Solo nel vuoto D. Solo per il sistema Terra – Luna E. Quesito senza soluzione univoca o corretta