La
legge
Gravitazione
Universale
di
Portfolio
a cura di Angela Maria De Santis
Specializzanda SSIS IX Ciclo I anno
Indirizzo FIM AA 2007-2008
La legge di Gravitazione Universale
Introduzione
Sono certa che se mi fossi trovata a lavorare in una scuola prima di frequentare la SSIS avrei
impostato ed affrontato l’intervento didattico in modo differente; mi sarei concentrata
esclusivamente sui contenuti disciplinari studiati nei corsi di fisica universitari cercando il
modo di adattarli per poterli sviluppare nella scuola superiore. Avrei svolto prevalentemente
lezioni frontali prive di una certa interattività, prive di illustrazioni sperimentali, prive di
metodologie didattiche alternative.
Ma grazie a questi due anni di SSIS scopro che l’allievo, centro del processo di
insegnamento-apprendimento, deve essere protagonista e responsabile del suo
apprendimento; mentre il docente è “solo” il facilitatore, il tramite. Il compito del docente è
quello di rielaborare il sapere, trasformarlo ed adattarlo alla realtà, unica e singolare della
propria classe, preparando l'ambiente per una situazione capace di produrre effettivamente
l’apprendimento di concetti disciplinari.
Adottare come metodologia esclusivamente la lezione di tipo frontale non stimola gli
allievi, non li aiuta a diventare delle parti attive di questo processo, non li conduce alla
riflessione attiva, bisogna indurre negli allievi delle rotture cognitive che attivino il loro
bisogno di raggiungere determinati obiettivi visti e sentiti come propri.
Dopo questo interessante percorso durato due anni, dove ho potuto studiare e scoprire la
didattica, la pedagogia e la psicologia, voglio e devo cambiare il mio punto di vista, cercherò
quindi di mettere il destinatario al centro, cercando, per quanto mi è possibile, di trasmettere
i contenuti in modo attivo, trovando situazioni che gli allievi possono sperimentare in modo
da sentirsi coinvolti e che li aiutino a tenere vivo il livello della comunicazione.
L’idea è di guidare gli allievi alla scoperta dei contenuti adottando una metodologia che
li stimoli attraverso semplici analogie, esempi, riflessioni, gli affascinanti esperimenti ideali e
realizzando dove possibile dei semplici esperimenti con l’ausilio di oggetti facilmente
reperibili.
Contenuti
La pubblicazione, nel 1687, dei Philosophiae Naturalis Principia Mathematica di Newton
segnano l’inizio di una fase di grandi scoperte che, per quasi due secoli, si muoveranno entro
uno schema dominato dal modello newtoniano. Solitamente, per ragioni di tipo prettamente
didattico, nei libri di fisica si segue uno schema entro il quale si “costruisce” quasi tutta la
meccanica (descrizione del moto, cause dei cambiamenti nel moto, leggi della dinamica) e poi, al
termine, si parla della gravitazione. Anche se tale modo di procedere da un lato risulta più
semplice, perché le difficoltà di comprensione del significato di alcune grandezze fisiche vengono
diluite, dall’altro non è corretto sul piano storico. Tuttavia ritengo che sia preferibile presentare
la legge newtoniana di gravitazione solo dopo aver sviluppato i fondamenti della meccanica
poiché in questo modo gli studenti hanno modo di assimilare le nozioni di meccanica proprio
perché diluite.
UNITÀ 1
•
•
•
•
•
•
•
•
•
La gravità Newtoniana
Moti del Sole
La prima soluzione geocentrica
La teoria eliocentrica
Le Leggi di Keplero e la Gravitazione Universale
La determinazione di G
Concetto di campo
Lavoro della forza gravitazionale
Energia nel moto planetario
Che altro possiamo fare con la legge di gravitazione ?
UNITÀ 2
La gravità di Einstein
2
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
•
•
•
•
•
•
Due postulati fondamentali della relatività ristretta
Trasformazioni di coordinate in meccanica relativistica - Trasformate
di Lorentz
Dilatazione dei tempi e contrazione delle lunghezze
Il principio di equivalenza
Conseguenze del principio di equivalenza - Effetto della gravità sulla
luce
Fisica e geometria
Prerequisiti:
Per trattare l’argomento credo sia essenziale come prerequisiti base:
la forza e il moto
o i principi della dinamica,
o massa e peso,
o equazioni del moto circolare uniforme,
o forza centripeta e moto circolare,
o principi della dinamica,
o moto dei proiettili;
lavoro ed energia
o lavoro di una forza,
o concetto di energia, energia cinetica, energia potenziale,
o conservazione dell’energia meccanica,
o forze conservative e dissipative.
Competenze:
Conoscere le varie soluzioni date storicamente al problema del moto dei pianeti, in
particolare il modello tolemaico e il modello copernicano.
Conoscere gli sviluppi moderni del problema del moto dei pianeti e i contributi dovuti a
Tycho Brahe, Galileo e Keplero.
Conoscere il significato e l'importanza della legge di gravitazione universale.
Saper applicare la legge di gravitazione universale alla soluzione di problemi relativi alla
massa dei pianeti, all'accelerazione di gravità e al moto dei pianeti e dei satelliti.
Conoscere il concetto di campo gravitazionale e, a grandi linee, la spiegazione eisteiniana
della gravità.
3
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
UNITÀ 1
La gravità Newtoniana
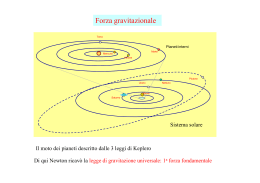
Newton arriva a postulare l’esistenza della gravitazione universale come causa dei moti celesti
nello stesso istante in cui afferma che le accelerazioni sono l’effetto di forze. I maggiori successi
della meccanica newtoniana si ebbero infatti nella definitiva comprensione del moto dei pianeti
nel Sistema Solare. Prima quindi di approfondire ulteriormente il problema della gravità, alla
luce della Legge di Gravitazione Universale di Newton, facciamo un passo indietro e vediamo
come erano descritti i moti dei pianeti nei principali sistemi pre-newtoniani.
Moti del Sole
I fenomeni celesti, si svolgono anche oggi nella stessa maniera che al tempo dei Greci; una
caratteristica affascinante di questa parte della fisica è il fatto che voi potete osservare a occhio
nudo la maggior parte di quello che i primitivi scienziati videro e annotarono, e potete scoprire
alcuni di quei cicli e cambiamenti ritmici conosciuti da così lungo tempo: il cambiamento
stagionale dell'altezza del Sole a mezzogiorno, le fasi mensili della Luna e il maestoso spettacolo
del lento ruotare del cielo notturno.
Per un osservatore sulla Terra, il più importante ciclo celeste è indubbiamente quello del
susseguirsi del giorno e della notte. Ogni giorno il Sole sorge al di sopra dell’ orizzonte locale,
nella parte del cielo rivolta a Est e tramonta verso Ovest. Nel suo moto quotidiano, il Sole
descrive un arco attraverso il cielo, simile a quello rappresentato nel disegno in figura 1.
Figura 1.
Oltre al Sole e alla Luna, è possibile osservare cinque corpi alquanto luminosi che si muovono in
mezzo alle stelle, chiamati pianeti. Sono: Mercurio, Venere, Marte, Giove e Saturno. Con l'aiuto
del telescopio ne sono stati scoperti in seguito altri tre: Urano, Nettuno e Plutone.
La prima soluzione geocentrica
Fin dall'antichità si riteneva che la Terra fosse al centro dell'universo e che le stelle ruotassero
intorno ad essa. Aristotele sostenne che la forma dei corpi celesti, così come quella delle loro
traiettorie, dovesse essere la più perfetta, cioè quella circolare.
Nell'applicazione di tale teoria al moto dei pianeti, sorsero però delle difficoltà che furono
superate con l'impegno degli scienziati in circa due millenni. Il moto dei pianeti osservato dalla
Terra, infatti, descrive sulla volta celeste orbite complesse, con velocità e direzioni variabili: moto
retrogrado (figura 2). Le traiettorie dei pianeti erano perciò in contraddizione con la teoria del
moto circolare e furono escogitate varie teorie che spiegavano la forma di tali traiettorie come
combinazione di opportuni moti circolari.
Figura 2. Moto retrogrado di un pianeta rispetto alla Terra.
La teoria più completa di tipo geocentrico, con la Terra cioè al centro dell'universo, fu quella di
Tolomeo. Analizzando la traiettoria annuale del Sole, ci si rende conto che qualsiasi soluzione
basata su un semplice sistema circolare con velocità uniforme è da scartare.
4
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Come si spiega la variazione di velocità nel moto dei pianeti e il moto retrogrado?
Tolomeo credeva che la Terra fosse al centro dell'Universo, tuttavia non riteneva che fosse al
centro esatto; egli propose invece che il centro C di un cerchio potesse non coincidere con il
centro della Terra; cioè che la Terra fosse in posizione eccentrica. Perciò, un moto che in realtà
era uniforme rispetto al centro C, osservato dalla Terra sarebbe apparso non uniforme.
Anche se l'eccentrico spiegava piccole variazioni della velocità, certo non era in grado di
spiegare cambiamenti così radicali come quelli che si osservano nel moto retrogrado dei pianeti.
Per rendere conto anche del moto retrogrado, Tolomeo ricorse a un altro accorgimento: l’epiciclo.
Il pianeta si muove a velocità costante sulla circonferenza di un piccolo cerchio, chiamato
epiciclo; nel frattempo, il centro dell'epiciclo si muove attorno alla Terra a velocità costante sul
cerchio più grande, chiamato deferente.
Quando la velocità del pianeta sull'epiciclo è più grande della velocità sul cerchio maggiore, il
pianeta descrive degli anelli caratteristici, che hanno il massimo risalto se visti dall'alto.
Guardando da una posizione vicina al centro, gli stessi anelli appariranno analoghi ai moti
retrogradi osservati in realtà per i pianeti.
Illustrazione sperimentale:
Non è possibile imparare la fisica senza prendere contatto con qualche attività pratica che ti
permetta di “scoprire” oltre che di “capire”, quindi credo sia necessario che lo studio sia integrato
con l’esecuzione di esperimenti. Con modeste attrezzature è possibile costruirsi una macchina
per simulare il modello degli epicicli. Basta forare due bacchette di legno, come indicato nello
schema e inserire nei fori due tondini metallici che fungono da assi di rotazione.
Se si applica una piccola sorgente luminosa sulla bacchetta più corta, facendo ruotare il
deferente (la bacchetta più lunga) e, di conseguenza l'epiciclo, in un ambiente oscurato si vedrà
la lampadina descrivere un moto epicicloidale. La cosa è più evidente se la velocità di rotazione è
elevata.
La teoria eliocentrica
II modello geocentrico fu accettato quasi universalmente per un periodo di circa duemila anni
dall'epoca di Platone e Aristotele. Eppure un modello radicalmente diverso, basato su ipotesi
assai differenti, era stato proposto nel terzo secolo a.C. L'astronomo Aristarco suggerì che una
più semplice spiegazione del moto nei cicli sarebbe scaturita dal considerare il Sole al centro, e
la Terra, i pianeti e le stelle in rotazione attorno al Sole stesso. Una soluzione così concepita,
che pone cioè il Sole al centro dell'Universo, è denominata concezione eliocentrica.
5
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Si potevano inoltre spiegare i moti retrogradi dei pianeti, facendo l'ipotesi che la Terra e i
cinque pianeti visibili ruotassero attorno al Sole (moto di rivoluzione).
Dal disegno si può capire come questo sistema eliocentrico fosse in grado di spiegare i moti
retrogradi di Marte, Giove e Saturno (nel disegno si suppongono orbite circolari).
Nonostante tutto questo, la proposta di Aristarco fu completamente trascurata nell'antichità;
anzi fu severamente criticata per diversi motivi. Una critica veniva dal fatto che le osservazioni
dirette sembravano contraddire Aristarco. Se infatti la Terra fosse stata in moto su un'orbita
circolare attorno al Sole, essa si sarebbe mossa avanti e indietro rispetto alle stelle fisse; ma gli
astronomi greci non avevano osservato nulla di simile. Questo fatto imbarazzante poteva essere
spiegato in due maniere: o la Terra non gira attorno al Sole, oppure la Terra gira attorno al
Sole, ma le stelle sono talmente lontane che lo spostamento è troppo piccolo per essere
osservato. I Greci compresero che in quest’ultimo caso le stelle avrebbero dovuto essere
spaventosamente lontane da noi.
Quando la Terra sorpassa un pianeta, nella
sua corsa attorno al Sole, sembra che il
pianeta si sposti nel cielo in senso contrario.
Le frecce indicano le linee visuali del pianeta
per varie posizioni della Terra,
contrassegnate con numeri successivi. I
cerchietti numerati che compaiono in basso
danno le corrispondenti posizioni apparenti
del pianeta sullo sfondo delle stelle lontane.
L'astronomo Nikolaus Kepperlingk (1473-1543), che poi latinizzò il suo nome in Copernico,
riprese una teoria di Aristarco (III sec. a.C.) e fu il divulgatore della teoria eliocentrica, in base
alla quale il Sole è ritenuto immobile al centro dell'universo, mentre la Terra e i pianeti ruotano
su orbite circolari intorno ad esso. La teoria di Copernico provocò una crisi profonda nella
concezione dell'universo, sembrando inconciliabile con l'assunto filosofico e religioso della
centralità dell'uomo.
Dal punto di vista strettamente scientifico, il modello copernicano, che pure semplificava
notevolmente la descrizione del sistema solare, non si conciliava in maniera precisa con le
osservazioni astronomiche. Per trovare un miglior accordo con i dati sperimentali, anche
Copernico dovette ricorrere agli epicicli, giungendo a un modello altrettanto complicato e
artificioso come quello tolemaico.
La disputa tra i sostenitori delle due teorie divenne sempre più accesa, soprattutto quando
l'intervento di Galileo a sostegno della teoria eliocentrica, mirato a convincere gli esponenti della
Chiesa cattolica ad accettarla e propagandarla, sortì l'effetto opposto. Infatti ben presto le opere
a favore dell'eliocentrismo furono considerate eretiche e condannate dalla Chiesa.
Le Leggi di Keplero e la Gravitazione Universale
Le resistenze ad accettare il sistema eliocentrico sono testimoniate dal grande Tycho Brahe che
fu un acutissimo osservatore ed accrebbe notevolmente la precisione delle misure ad occhio
nudo prima che Galileo usasse il cannocchiale.
L'importanza dell'opera di Tycho Brahe risiede soprattutto nella sua imponente raccolta di dati
sperimentali, frutto di osservazioni astronomiche di estrema precisione.
Keplero fu assunto nel 1600 come assistente di Tycho con il compito di verificare i dati
sull’orbita di Marte; egli cercava conferme della teoria eliocentrica; i dati sperimentali di Tycho
Brahe diedero la possibilità al suo assistente Keplero di determinare, dopo una lunga
elaborazione, le effettive orbite dei pianeti intorno al Sole senza ricorrere agli epicicli; Keplero si
accorse che queste orbite non erano circolari ma ellittiche.
Egli formulò così quella che è nota come Ia Legge di Keplero: I pianeti descrivono intorno al Sole
delle orbite ellittiche, di cui il Sole occupa uno dei fuochi.
6
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Nell'orbita di un pianeta (fìg. 3), il punto più lontano e quello più vicino al Sole sono detti
rispettivamente afelio e perielio.
Figura 3.
L’opera di Keplero fa sorgere una domanda: “perché le orbite planetarie sono ellissi?”; tale
domanda rimase senza un’adeguata risposta per circa ottant’anni, fino a quando Newton
mostrò che le orbite ellittiche derivano di necessità da una legge più generale.
La prima legge di Keplero indicava la forma generale delle orbite dei pianeti ma non
consentiva di giustificarla, Keplero cercò comunque di risalire alla relazione tra la posizione di
un pianeta e la sua velocità. Inizialmente egli stabilì che la velocità di un pianeta è maggiore
quando la sua orbita è più vicina al Sole (perielio) e minore quando è più distante (afelio) ed
infine giunse alla IIa Legge di Keplero: II raggio vettore tracciato dal Sole a uno qualsiasi dei
pianeti descrive aree uguali in intervalli di tempo uguali.
La seconda legge di Keplero può essere formulata in modo equivalente dicendo che l'area
descritta dal raggio vettore di ogni pianeta nell'unità di tempo, detta anche velocità areolare,
è costante durante il moto del pianeta sull'orbita.
Nella figura 4 sono rappresentate l'area descritta dal raggio vettore in un certo intervallo
di tempo quando il pianeta si muove intorno all'afelio e quella descritta in un intevallo di
tempo uguale intorno al perielio. Poiché le due aree sono uguali, è evidente che il pianeta
percorre, nell'intervallo di tempo dato, un cammino più breve in prossimità dell'afelio e più
lungo in prossimità del perielio. Da questo segue che la velocità lineare con cui il pianeta
percorre l'orbita ellittica è minima nell'afelio e massima nel perielio.
Figura 4.
Per parecchi anni Keplero si dedicò a cercare una terza legge che ponesse in relazione tutte le
orbite planetarie, e guidato dalla sua fiducia nella rappresentazione matematica della natura,
si ostinò a confrontare i dati astronomici relativi ai diversi pianeti arrivando così alla legge dei
periodi che lega i periodi dei pianeti alla loro distanza dal Sole. IIIa Legge di Keplero: I
quadrati dei tempi di rivoluzione dei pianeti intorno al Sole sono proporzionali ai cubi dei
semiassi maggiori delle rispettive orbite.
dove la costante K ha lo stesso valore per tutti i pianeti.
Le leggi di Keplero descrivono compiutamente il moto dei pianeti, ma non ne risalgono alle
cause. La definitiva accettazione, nella seconda metà del’600 del principio di inerzia, pose il
problema in termini diversi: una traiettoria chiusa, circolare o ellittica, richiede l’esistenza di
una forza diretta verso il centro dell’orbita. Nel caso dei pianeti suggerisce l’esistenza di una
forza attrattiva diretta verso il Sole.
L'idea di una proprietà inerente alla natura dei fenomeni si era comunque affermata
quando Newton (1642-1727) elaborò la teoria della gravitazione universale.
Newton riconosce un debito culturale solo nei confronti della III legge di Keplero perché in
virtù di essa, cioè della regolarità tra periodo e distanza al cambiare del pianeta, può
affermare il carattere unitario della forza di interazione tra Sole e pianeti. A questo punto
7
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
passa alla generalizzazione ed afferma che si tratta della stessa forza che spiega il moto del
sistema Terra Luna e del sistema di Giove e dei suoi satelliti.
Ma Newton come ci arriva?
Per dare un’idea del tipo di ragionamenti condotti da Newton supponiamo che, in prima
approssimazione, i pianeti ruotino intorno al Sole di moto uniforme in orbite che differiscono
molto poco da circonferenze.
Ma se il moto del pianeta è circolare uniforme esiste un’accelerazione centripeta diretta
verso il centro dell'orbita, cioè verso il Sole. Dalla II legge della dinamica sappiamo che una
tale accelerazione è dovuta all'azione di una forza; dunque il Sole agisce su ogni pianeta con
una forza diretta verso di sé. Dalla validità della III legge della dinamica segue inoltre che il
Sole subisce a sua volta l'azione di una forza opposta alla precedente ed esercitata dal
pianeta. In base alla III legge di Keplero il rapporto tra il raggio orbitale al cubo e il quadrato
del periodo è costante, cioè:
La forza necessaria per mantenere un pianeta sulla sua orbita è data da:
Ed essendo l’orbita circolare:
Per la legge dei periodi e quindi:
4 4 1
Con C costante uguale a 4π /k. Poiché la quantità tra parentesi è costante, cioè è la stessa per
tutti i pianeti, si ha che la forza è direttamente proporzionale alla massa del pianeta e
inversamente proporzionale alla sua distanza dal Sole.
Ma la forza che attira i pianeti verso il Sole è la stessa che fa cadere i corpi sulla
Terra?
Inoltre Newton si chiese se la forza che attira i pianeti verso il Sole non potesse essere la
stessa che fa cadere i corpi sulla Terra. In un primo tempo mise alla prova questa sua
congettura considerando l'attrazione della Terra sulla Luna. Dai dati allora disponibili,
Newton sapeva che la distanza del centro della Terra dal centro della Luna era circa 60 volte il
raggio terrestre. Dallo studio dei gravi si conosceva già da lungo tempo che l'accelerazione di
gravità alla superficie terrestre vale circa 9,8 !. Newton calcolò che l’accelerazione della Luna
dovuta alla gravità terrestre dovesse essere pari a 1/60 1/3600 delll’accelerazione di gravità
sulla superficie terrestre, quindi con l'accelerazione di 9,80/3600 2,72 x 10( m/s . Newton
basandosi sulla conoscenza del periodo orbitale della Luna, della distanza Terra Luna e sulle
leggi del moto circolare uniforme ottenne per il valore dell'accelerazione: 2,74 + 10( /, .
Dunque, la forza che tiene la Luna sulla sua orbita diventa, proprio alla superficie della
Terra, uguale alla forza di gravità di cui noi possiamo osservare gli effetti sui corpi
pesanti. E perciò la forza che tiene la Luna sulla sua orbita è proprio la stessa forza che
noi chiamiamo comunemente gravità.
Questo è veramente un risultato eccezionale. La stessa forza che provoca la caduta di
una minuscola mela dall'albero è capace di mantenere la Luna sulla sua orbita!
Il discorso sul confronto tra l’accelerazione di gravità sulla Terra con l’accelerazione
della Luna è un discorso che bisognerebbe fare, e se non si fa, si perde il sapore di che cosa è
la fisica.
Vera o immaginaria che fosse la folgorazione dovuta alla caduta della mela, Newton intuì che
la caduta dei gravi è dovuta ad una forza di attrazione della Terra e gli parve ragionevole
supporre che questa forza non si limitasse ai rami di un albero, ma si estendesse al di là di
8
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
essi a quote sempre maggiori, fino alla Luna. D'altra parte, il principio di azione e reazione, da
lui stesso stabilito, imponeva allora che anche la mela, o la Luna esercitassero a loro volta
sulla Terra una forza uguale e contraria. Estendendo questo ragionamento, gli parve naturale
pensare che tutti i corpi dell'universo si attraessero tra loro con una forza della stessa natura.
Il terzo principio della dinamica ci dice che non vi è un corpo che attrae e uno che viene
attratto, ma che l'attrazione deve essere reciproca: sul Sole deve agire una forza identica a
quella che agisce sul pianeta; e diretta in senso opposto.
F./ C 1
M
R
e per il principio di azione e reazione F./ F/. la forza di attrazione reciproca diventa allora:
FG
Mm
R
Quando una persona tiene in mano un sasso a una certa altezza e poi lo lascia cadere, il
sasso accelera verso il suolo. Le nostre leggi del moto ci assicurano che deve esistere una
forza agente sul sasso che lo fa accelerare verso la Terra. Conosciamo la direzione di tale
forza, e siamo in grado di trovare la sua intensità moltiplicando la massa del sasso per
l'accelerazione. Possiamo contraddistinguere questa forza con il nome di peso o di attrazione
gravitazionale terrestre, ma ciò non risolve il problema del perché esista questa interazione
tra i corpi.
Newton non si limitò ad affermare che una sola, semplice legge descriveva tutte le forze
esistenti tra il Sole e i pianeti: egli riteneva infatti che non vi fosse niente di speciale o di
eccezionale nel caso dei corpi del sistema solare, o della Terra e della mela: perciò, un'identica
relazione doveva valere per quasiasi altra coppia di corpi, posti a una distanza notevole
rispetto alle loro dimensioni, e in qualsiasi parte dell'Universo si trovassero. Egli propose cioè
una legge generale della gravitazione universale, che può essere così espressa:
F5678 G
m9 m
R
La trattazione precedente non può essere considerata come una deduzione della legge di
gravitazione universale, ma serve solo ad illustrare la linea di ragionamento seguita da
Newton. Tra l’altro, alcune delle pause nel lavoro di Newton sono proprio legate alla necessità
cruciale di dimostrare in maniera inoppugnabile quello che per noi appare quasi una ovvietà,
ma che tale non è, e cioè il fatto che dal punto di vista gravitazionale gli effetti di una sfera di
dimensioni finite o quelli di una massa puntiforme, siano identici. Il fattore G nella legge di
gravitazione universale è detto costante di gravitazione universale; il suo valore è pari alla
forza di interazione tra due masse unitarie che si trovino a distanza unitaria e può essere
determinato per via sperimentale.
La determinazione di G
Nel 1798 lo scienziato inglese Henry Cavendish (1731-1810) eseguì un esperimento per
misurare in laboratorio l’attrazione gravitazionale e quindi determinare la costante di
gravitazione. L'apparato sperimentale era costituito da una bilancia di torsione il cui
funzionamento è schematizzato in figura 5.
Il valore determinato fu di 6.675 < 10(99
=!
>5!
. Si osservi che, nel caso della bilancia di
torsione, si fa esplicito uso di un risultato già determinato da Newton, quello secondo cui i
corpi sferici e omogenei sono sempre assimilabili a puntiformi anche quando le loro
dimensioni, rispetto alle distanze in gioco, non consentirebbero tale affermazione.
Conoscendo G da questo esperimento possiamo indirettamente conoscere il valore della
massa della Terra.
Perché nella vita quotidiana non rileviamo gli effetti della legge di gravitazione?
9
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
A questo punto farei osservare che il valore della costante G fa sì che la forza gravitazionale
che si esercita tra corpi di dimensioni e massa ordinari sia difficilmente rilevabile.
Figura 5. Schema del dispositivo di Cavendish per la misura della costante di attrazione gravitazionale.
Concetto di campo
Dopo il 1800 incominciò a farsi strada il concetto di campo. In questo caso una o più masse
generano nello spazio un campo gravitazionale e un'altra massa m, chiamata massa di prova
posta in un punto dello spazio, risente dell'azione di una forza F. II campo gravitazionale
generato in un punto da un sistema di masse è il vettore g=F/m dato dal rapporto fra la forza
gravitazionale F, agente sulla massa di prova m posta in quel punto, e la massa m. È
importante sottolineare che il campo gravitazionale esiste indipendentemente dalla presenza
della massa di prova. Essa è solo un mezzo atto a rivelare l'esistenza del campo gravitazionale
in un determinato punto dello spazio tramite la forza F agente su di essa.
Analogia
Per chiarire meglio il concetto facciamo un esempio:
supponiamo di essere in prossimità di uno specchio di acqua nel quale sta galleggiando un
sughero. Potremmo far muovere il sughero, inizialmente fermo, iniziando a colpire l’acqua con
un altro sughero in un punto anche relativamente distante dal primo. Se guardiamo solo i
due sugheri possiamo concludere che l’uno si muove dopo un certo tempo in risposta al moto
dell’altro. Tra i due corpi vi è dunque un’interazione; ovviamente noi non abbiamo fatto altro
che perturbare l’acqua la quale a sua volta ha interagito con l’altro sughero. L’acqua in
questo esempio, fa le veci del campo.
Consideriamo la Terra e usiamo una piccolo corpo di massa m come sonda del campo
gravitazionale, se questo corpo si trova in prossimità della Terra subirà una forza che ha
modulo, direzione e verso ben definiti in ciascun punto dello spazio. Il modulo è mg e la
direzione è radiale verso il centro della Terra. A ciascun punto in prossimità della terra
possiamo associare un vettore g che rappresenta l’accelerazione subita da un corpo lasciato
libero in tale punto. Si definisce intensità del campo gravitazionale in un punto come g=F/m.
Indicando con M? la massa della Terra, il campo gravitazionale a distanza r dal suo
A
centro, è diretto verso il centro della Terra e ha intensità g G !B
6
L'intensità del campo dipende dalla massa della Terra e dalla distanza. In particolare per
r R ? , raggio terrestre, dall'equazione scritta sopra otteniamo l'accelerazione di gravità sulla
superficie della Terra, che qui indichiamo con g D :
EF G
HI
JKI
(1)
il cui valore ben noto è uguale a L, MN O/P K . Eseguendo il rapporto membro a membro delle
due equazioni precedenti ricaviamo:
JKI
E EF K
Q
che ci permette di confrontare l'accelerazione di gravità g in un punto a distanza r dal centro
della Terra con l'accelerazione E F sulla superficie terrestre. In funzione dell'altezza h dal
suolo, l'accelerazione di gravita è espressa dalla relazione:
g
g D R?
R ? R h
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
10
Ottenuta ponendo r R ? R h . Si comprende facilmete il motivo per cui l’accelerazione di
gravità per piccoli dislivelli può ritenersi con ottima approssimazione costante, ad esempio ad
un’altezza da terra di 100, g diminuisce soltanto di circa 0.2 /, .
C'è inoltre un altro aspetto interessante da esaminare: l'azione del campo si propaga nello
spazio a una velocità finita, uguale a quella della luce.
Supponiamo che il Sole esploda, che cosa succederà alla Terra?
Secondo la teoria del campo gravitazionale di Einstein, nessun corpo o segnale può viaggiare
a una velocità superiore a quella della luce; quindi per 8 minuti circa (il tempo che impiega la
luce a percorrere la disianza Sole-Terra) noi continueremmo a vedere il Sole e la Terra
continuerebbe regolarmente la sua orbita, come se niente fosse successo, e in effetti per noi
sulla Terra nulla sarebbe (ancora) successo. Dopo 8 minuti vedremmo e percepiremmo la
catastrofe e la Terra uscirebbe dall'orbita lungo la tangente. Effettivamente, il campo si
propaga nello spazio come un'onda nel mare o l'onda d'urto di un'esplosione, raggiungendo a
una velocità finita e in un tempo finito, ma diverso da zero, tutti i punti dello spazio. Il campo
quindi ha un'esistenza per così dire "autonoma" anche dalla sua sorgente: la perturbazione
gravitazionale continuerebbe a propagarsi nello spazio anche dopo che il Sole avesse cessato
di esistere, così come possiamo vedere la luce emessa da stelle lontane anni luce e che
potrebbero essere ormai scomparse quando la loro luce giunge fino a noi.
Lavoro della forza gravitazionale
Calcolando l’energia potenziale U di un corpo posto ad un’altezza h rispetto ad una
qualsisi quota di riferimento si ottiene il risultato T UV che è corretto nell’ipotesi in cui
g si mantenga costante, cosa che è sicuramente vera se rimaniamo in prossimità della
superficie terrestre. Poiché come abbiamo visto il valore di g dipende dal valore di r
(distanza dal centro della terra)
ci chiediamo quanto sia la variazione dell’energia
potenziale nel caso più generale di un corpo che venga spostato, lungo la verticale, da un
punto ad un altro nello spazio a distanze non trascurabili rispetto al raggio terrestre.
Se un corpo di massa m cade verticalmente dalla posizione A alla posizione B, a distanze
WX ed WY , rispettivamente, dal centro della Terra, per calcolare la variazione di energia
potenziale bisogna valutare il lavoro fatto per portare la massa m da A in B; dividiamo lo
spostamento WX – WY in tanti piccoli intervalli in modo da poter considerare costante la forza
gravitazionale. Si calcola il lavoro e si ottiene:
[ \]^ _
1
1
` a.
WY WX
Si può dimostrare anche che il lavoro è sempre lo stesso per una fissata coppia di punti A
e B, dipende soltanto dalle distanze WX e WY dal centro della Terra; la forza gravitazionale è
conservativa. Ricordiamo che, per ogni forza conservativa, il lavoro compiuto dalla forza
quando il suo punto di applicazione si sposta da A a B, indipendentemente dal cammino
percorso, è [ TX ` TY . Dal confronto di questa equazione con la precedente deduciamo
che
1
1
bT `[XY \]^ _ ` a
WX WY
Se ora immaginiamo che il punto A si trovi ad una distanza da B sufficientemente grande
(in teoria a distanza infinita) e stabiliamo che a tale distanza il valore dell'energia
potenziale sia zero allora nell'espressione che dà il lavoro avremo:
[ `\
]^
`TY
WY
Potremmo dunque definire l'energia potenziale in un punto come il lavoro che le forze del
campo devono eseguire per portare il corpo in quel punto.
11
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Il segno meno indica che, con questa scelta della configurazione di riferimento e del
corrispondente valore dell’energia potenziale, l’energia potenziale è negativa per qualsiasi
distanza finita tra i due corpi, questo significa che essa è nulla all’infinito e diminuisce al
diminuire della distanza. Ciò corrisponde al fatto che la forza gravitazionale esercitata da
] su è attrattiva.
A questo punto ci interessa mostrare come sia possibile ricondursi all’espressione
T UV se V c . Calcoliamo la variazione di energia potenziale di un oggetto la cui
posizione varia dall’altezza h sopra la superficie terrestre della Terra alla superficie stessa.
Otteniamo:
R V ` 1
1
\] \]
R
\] _ `
a \] d
e·
bT `
RV
R V
RV
Se vale l’ipotesi V c , allora R V g . Inoltre, dalla relazione ( 1 ) sappiamo che
hA
g ! per cui, sostituendo nella relazione precedente si ottiene
i
h
ΔU g R m gmh
R
che, coincide con l’usuale espressione dell’energia potenziale gravitazionale.
Energia nel moto planetario
Illustrazione sperimentale: l’interazione gravitazionale potrebbe far ruotare il Sole
attorno alla Terra?
Qualche studente potrebbe chiedere, come mai noi dovremmo immaginare la Terra in
rotazione attorno al Sole quando l’interazione gravitazionale potrebbe far ruotare il Sole
attorno alla Terra. Qui è nascosta una fenomenologia fisica di grande importanza e
bisognerebbe stimolare questa domanda nel caso in cui non nascesse spontaneamente.
È possibile gestire questo problema in maniera del tutto qualitativa: inizialmente si
potrebbe partire chiedendo come mai crediamo che la Terra e i pianeti compiano delle
rivoluzioni attorno al Sole e non viceversa. Qualche giorno dopo aver proposto la questione
e aver dato modo agli studenti di pensarci, proporrei agli studenti di prevedere quale sarà
la posizione del centro del moto circolare di due dischi identici legati tra loro e a cui ho
impresso una spinta (possibilmente su un tavolo a cuscino d’aria) in modo da farli tendere
a muoversi di moto circoalre con la minima traslazione possibile. Dopo aver stabilito il
comportamento dei dischi identici passo a porre un peso su uno dei due dischi e chiedo
ancora di prevere il comportamento. Successivaemnte passo a porre un peso molto più
pesante sul disco sperando che ora emerga chiaramente l’aspettativa di un centro di
rotazione che sia molto vicino al centro del disco più pesante e che gli studenti vedano
chiaramete l’analogia con la Terra e il Sole.
Se indichiamo con la massa di un corpo in movimento con velocità nel campo
gravitazionale terrestre e con W la sua distanza dal centro della Terra, per il principio di
conservazione dell'energia meccanica possiamo scrivere:
9
` \
lmn
o
pq,rsrt
(2)
cioè la somma dell'energia cinetica e dell'energia potenziale del corpo si mantiene costante
durante il moto. Supponiamo ora che il corpo in esame sia un satellite in orbita circolare
di raggio r intorno alla Terra (figura 6).
Figura 6.
12
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Per la seconda legge della dinamica, l'accelerazione centripeta v /r cui è sottoposto il
satellite, moltiplicata per la sua massa m, deve essere uguale alla forza gravitazionale
esercitata su di esso dalla Terra, cioè:
M? m
v
G m
r
r
Ne segue che l'energia cinetica del satellite è:
Ew G
M? m
2r
Pertanto l'energia totale E = Ec + U diventa:
E `G
AB 6
(3)
II risultato fondamentale che a questo punto si vuole evidenziare è che il satellite ha
energia totale negativa; ciò significa che il sistema si trova in uno stato legato, il corpo m
rimane legato al corpo M che lo attrae senza sfuggirgli.
La condizione che deve essere rispettata, affinchè a un sistema di due masse possano
essere applicate equazioni come la ( 2 ) o la ( 3 ), è che la massa del corpo che genera il
campo sia molto maggiore della massa m in movimento nel campo. In questo caso, allora,
la massa più grande può essere ritenuta immobile nella posizione che occupa in un
sistema di riferimento inerziale e la sua enegia cinetica può essere perciò trascurata. In
caso contrario, nello scrivere l'energia totale del sistema, dovremmo includere anche
l'energia cinetica di questa massa.
Nel caso della Terra, la condizione ]^ x è certamente verificata se m è la massa di un
satellite artificiale. Relativamente al sistema Terra-Luna, le due masse differiscono solo
per due ordini di grandezza e la condizione è verificata più debolmente. Tuttavia, anche in
questo caso, l'approssimazione di considerare ferma la Terra è accettabile e comporta un
errore trascurabile.
Che altro possiamo fare con la legge di gravitazione ?
C’è infine un altro aspetto importante da mettere in risalto e cioè il potere predittivo della
teoria che culmina con la scoperta di Nettuno. Questo è per esempio un aspetto di cui si
parla poco, spiegare perché i pianeti non seguono esattamente le leggi di Keplero; quando
nel 1820 si soprì il carattere anomalo di Urano, gli astronomi si divisero tra quelli che
pensavano che doveva esserci un altro pianeta e quelli che credevano che forse la legge di
gravità a grandi distanze non era più esatta. Anni di lavoro produssero una previsione,
doveva esistere un altro pianeta e dopo aver calcolato dove avrebbe dovuto trovarsi un
pianeta simile per produrre le perturbazioni osservate, fu scoperto Nettuno. Questa è la
conferma che la legge di gravitazione funziona, perché il pianeta c’è e con la presenza di
quel pianeta si spiega il moto di Urano.
Penso che questa storia debba essere raccontata perché fa capire che la fisica non è pura
induzione dagli esperimenti, né formulazione di principi seguita da una deduzione logica;
è un intreccio di entrambe le cose.
13
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
UNITÀ 2
La gravità di Einstein
Lo sviluppo della gravità newtoniana, ha avuto applicazioni di notevole successo; ad
esempio ci fornisce gli strumenti per determinare con notevole precisione il moto dei corpi
nei campi gravitazionali. Il superamento di essa si ebbe agli inizi del XX esimo secolo con
Einstein e la Relatività Generale (RG). Arrivati a questo punto della trattazione la grossa
tentazione che si ritrova anche in acuni libri è quella di dare direttamente dei cenni della
senza parlare di Relatività ristretta (RR); così facendo però si corre il rischio di dare agli
studenti delle misconcezioni perché non si mostra loro l’inadeguatezza del nostro concetto
di tempo e di spazio; ci sono infatti dei fenomeni che non possono essere spiegati dalla
fisica newtoniana per cui è indispenasbile parlare di RR la quale ha la reputazione di
essere una materia molto difficile; probabilmente l’aspetto più impegnativo della RR sta
proprio nel fatto che bisogna cambiare le nozioni di spazio e tempo acquisiti dalla nostra
“esperienza quotidiana”. Senza entrare nel dettaglio di una teoria fisico-matematica tanto
complessa indichiamo alcuni dei punti principali su cui essa è basata.
Relatività e senso comune
Mentre nella meccanica newtoniana ogni mutua azione si manifesta istantaneamente,
qualunque sia la distanza fra i corpi interagenti, le forze elettromagnetiche descritte nella
teoria di Maxwell si propagano con una velocità finita, corrispondente a quella della luce.
Proprio per questo, si comprese ben presto la necessità di elaborare una teoria che riunisse sotto una stessa logica i principi della meccanica e dell'elettromagnetismo e che
avrebbe rivoluzionato la fisica classica; tale teoria è la relatività einsteiniana.
Nel 1905 Albert Einstein pubblicò la teoria della relatività ristretta o speciale, che tratta di
come gli oggetti e gli eventi siano osservati da sistemi di riferimento inerziali, modificando
nella logica e nelle conseguenze il modo in cui lo stesso argomento era stato affrontato da
Galileo e da Newton. Nel 1916 Einstein completò la sua opera con la pubblicazione della
teoria della gravitazione, o teoria della relatività generale.
Ma anche in meccanica classica si parla di relatività:
Il principio di relatività classica afferma che in tutti i sistemi di riferimento inerziali i
fenomeni meccanici avvengono con identiche modalità. Inoltre, quando uno stesso evento
è visto da sistemi inerziali differenti, le osservazioni sono messe in relazione mediante la
composizione vettoriale delle velocità e degli spostamenti: se v è la velocità di un corpo in
un certo sistema di riferimento inerziale, e v' è la sua velocità in un secondo sistema in
moto con velocità di trascinamento costante v, rispetto al primo, allora si ha:
v vy R v
(4)
Questa equazione, insieme all'analoga legge di composizione degli spostamenti, è
senz'altro appropriata per piccole velocità. Quando invece le velocità in gioco si avvicinano
a 3,00 • 10{ m/s, velocità della luce nel vuoto, si entra nel campo della fisica relativistica,
con conseguenze sorprendenti e in netto contrasto con l'esperienza di ogni giorno.
Anche se lontana dal senso comune, la relatività eisteiniana non è tuttavia una teoria
astrusa. A prescindere dal fatto che le sue previsioni hanno trovato dirette conferme
sperimentali, essa è di per sé un argomento affascinante, che ci offre un modo nuovo di
guardare le cose che ci circondano, questo è un motivo importante per cui si dovrebbe
parlare di relatività anche nelle scuole superiori.
Nella seconda metà del XIX secolo, Maxwell aveva dimostrato che la luce si propaga con
una velocità finita pari a c 3 • 10{ m/s.
Maxwell aveva previsto che viaggiano alla velocità di 300 000 km/s. Ma misurata
rispetto a che cosa? a quale riferimento?
Esperiemto ideale: in che modo questo risultato può essere interpretato in termini di
relatività classica?
Supponiamo di trovarci all'interno di un vagone ferroviario che viaggia alla velocità di 100
14
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
km/h e lanciamo in avanti una palla alla velocità di 20 km/h. Un osservatore che si trova
fuori del treno vedrà la palla muoversi alla velocità di 120 km/h.
Invece di lanciare la palla, accendiamo una torcia (figura 7). Chiunque, fino alla fine
del XIX secolo, avrebbe assegnato alla velocità di propagazione del fascio di luce la
velocità c + 100 km/h. (Per merito di Einstein ora sappiamo che questo presupposto è
completamente errato.)
Figura 7.
Dando tuttavia per scontato che le velocità (compresa quella della luce) si compongano
secondo la relazione ( 4 ), sorge immediatamente il problema di stabilire in quale sistema
di riferimento la velocità della luce presenti proprio il valore previsto dalla teoria di
Maxwell.
Questo riferimento assumerebbe il carattere di un sistema privilegiato, escludendo così
la possibilità di estendere la relatività galileiana ai fenomeni elettromagnetici. In epoca
prerelativistica i fisici, erano convinti che la luce potesse propagarsi solo in presenza di
un mezzo. Non potendo ritenere che il mezzo in questione fosse l'aria, perché la luce del
Sole giungeva sulla Terra attraverso lo spazio, i sostenitori più intransigenti del
meccanicismo inventarono un ipotetico mezzo di propagazione, chiamato etere.
Questo fluido, che pervadeva tutto lo spazio, doveva essere l'unica cosa rigorosamente
priva di movimento nell'universo, cioè il sistema di riferimento privilegiato in cui la luce si
propagasse alla velocità c prevista dalla teoria di Maxwell.
A causa del principio di relatività galileiana (RGal), allora, la luce dovrebbe essere vista
arrivare in ogni sistema di riferimento inerziale con una velocità pari a c più (o meno) la
velocità del detto sistema di riferimento inerziale rispetto all'etere. Furono fatti diversi
esperimenti molto accurati per rilevare queste differenze di velocità della luce (fra tutti
menzioniamo quello di Michelson e Morley del 1881) ma tutti non rilevarono alcuna
differenza.
Due postulati fondamentali della relatività ristretta
Tutte le contraddizioni alle quali conduceva il modo di ragionare della fisica classica
furono spazzate via nel 1905, quando Einstein pubblicò la teoria della relatività speciale o
ristretta, valida nel caso di sistemi in moto rettilineo uniforme l'uno rispetto all'altro. Egli,
con la semplicità propria di tutti i grandi geni, per uscire dalla situazione di disagio venutasi a creare, propose due postulati, noti appunto come postulati della relatività
ristretta.
Primo postulato: il principio di relatività: Le leggi della fisica sono le stesse in tutti i
sistemi di riferimento inerziali.
Questo enunciato rappresenta l'estensione del principio di relatività anche ai
fenomeni elettromagnetici; esso include tutte le leggi della fisica e quindi va oltre il
principio di relatività di Galileo-Newton che riguarda solo le leggi della meccanica. Nel
postulato è insita una verità assiomatica: il presupposto einsteiniano che debbano
esistere, da sempre e per sempre, alcune leggi della natura rigorosamente valide in
qualsiasi luogo della Terra e, più in generale, dell'universo.
I risultati sperimentali portavano ad un assurdo dal punto di vista della RGal
perchè contraddicevano la regola di sommabilità delle velocità. Per risolvere il problema si
ipotizzò che la velocità della luce fosse la stessa in ogni sistema di riferimento inerziale e
che la RGal fosse valida solo per velocità piccole rispetto a c, come sono del resto le
velocità rilevabili nell'esperienza quotidiana. Si abbandonò quindi il concetto di etere e si
cercarono allora nuove trasformate per esprimere le relazioni fra le coordinate ed i tempi
in due diversi sistema di riferimento inerziali che soddisfacessero il principio di costanza
di c ed avessero come caso limite, per velocità piccole rispetto a c, le trasformate di
15
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Galileo.
Secondo postulato: la costanza della velocità della luce: La velocità della luce nel vuoto
è p 3,00 • 10{ /, in tutti i sistemi di riferimento inerziali, indipendentemente dal moto
della sorgente rispetto all'osservatore.
Trasformazioni di coordinate
Trasformate di Lorentz
in
meccanica
relativistica
-
Sappiamo che uno stesso oggetto può essere contemporaneamente in moto o fermo se a
osservarlo sono due soggetti diversi. Un albero si muove per il viaggiatore che osserva la
campagna dal finestrino di un treno in movimento. Lo stesso albero è fermo se a
osservarlo è un uomo seduto per terra, sotto la sua ombra. Diciamo cioè che le proprietà
del moto di qualsiasi corpo dipendono da chi osserva il movimento.
Lo scopo di questo paragrafo è quello di esaminare come devono essere messe in
relazione le descrizioni che due osservatori in moto relativo uniforme danno di uno stesso
evento secondo la teoria della relatività ristretta. Nel 1904, l'olandese Hendrick A. Lorentz
elaborò nuove equazioni di trasformazione fra le coordinate spazio-temporali di uno stesso
evento descritto in due sistemi di riferimento in moto relativo uniforme, per cercare di
giustificare l'esito negativo dell'esperimento di Michelson e Morley.
Queste relazioni, note come trasformazioni di Lorentz, trovarono la loro piena
giustificazione fisica con Einstein, in quanto deducibili dai due postulati fondamentali
della relatività ristretta. Esse hanno validità generale, qualunque sia il valore della
velocità relativa fra i due sistemi di riferimento, da zero a c. Consideriamo due sistemi di
riferimento inerziali (K e K') di cui K' si muove di velocità costante v rispetto a K:
Dovendo essere c = costante, le leggi di trasformazione di spazio e tempo non potranno
più seguire le regole dettate dall'esperienza quotidiana. Dobbiamo abbandonare i concetti
di spazio e tempo come di entità assolute, separate. Dobbiamo addirittura modificare il
concetto stesso di simultaneità. Le trasformate che soddisfano le condizioni suddette
legano matematicamente le misure di spazio e tempo relativi a due sistemi di riferimento
inerziali partendo dal presupposto che la velocità della luce sia costante nei due sistemi.
Le trasformate di Lorentz sono:
 ` r
€ y ~
‚1 ` ~
p
~
ƒ1 ƒ
…
„1 „

r` 
~ 1
p
~r ~
‚1 ` }
p
Le trasformate di Lorentz, per velocità v << c diventano identiche alle trasformate di
Galileo così come previsto. Analizzando le trasformate di Lorentz si deduce
immediatamente un risultato fisico fondamentale. Se v = c, i denominatori si annullano.
Ciò significa che la velocità della luce non è fisicamente raggiungibile da nessun sistema
di riferimento inerziale rispetto ad un altro. Nessun corpo può raggiungere la velocità
della luce che rappresenta quindi un limite naturale invalicabile. Le trasformazioni di
Lorentz presentano tuttavia notevoli differenze rispetto alle trasformazioni di Galileo. La
più significativa riguarda la coordinata temporale: mentre nelle trasformazioni classiche è
t 1 t , cioè il tempo rappresenta una grandezza assoluta, indipendente dal sistema di
16
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
riferimento, nelle trasformazioni di Lorentz t e t' assumono valori diversi. Questa
conseguenza rivoluzionaria determina una totale diversità fra la relatività Galileana (RGal)
e la RR. Precisamente, il valore t' assegnato alla coordinata temporale di un evento nel
sistema K' dipende sia dal tempo t, sia dalla coordinata x misurati in K. In altre parole,
spazio e tempo sono grandezze correlate, sono legate matematicamente fra loro e possono
essere considerati come facenti parte di una unica entità, lo spazio-tempo.
Dilatazione dei tempi e contrazione delle lunghezze
Assodato che il tempo non è assoluto, questa fondamentale grandezza fisica non può
scorrere con lo stesso ritmo in tutti i sistemi di riferimento. Con molta probabilità, se per
un osservatore un fenomeno dura un certo intervallo di tempo Δt per un altro, che si trovi
in movimento rispetto al primo, dovrà durare un tempo diverso Δty. Analogamente, anche
le lunghezze e le distanze, come gli intervalli dì tempo, sono delle grandezze relative, la cui
misura dipende dal moto dell'osservatore.
Consideriamo i nostri soliti sistemi di riferimento inerziali (K e K'). Consideriamo ora due
eventi che avvengono in un punto fisso rispetto a K' ma in due istanti diversi.
Quanto dura il medesimo intervallo di tempo visto da K?
Semplici calcoli a partire dalle trasformate di Lorentz portano al seguente risultato:
br bry
‚1 ` p
si osserva facilmente che a velocità piccole rispetto a c le durate praticamente coincidono. A
velocità via via maggiori l'intervallo temporale viene visto da K durare sempre di più.
Come affrontare questo argomento in una scuola superiore? Esperiemto ideale:
In una scuola superiore si può svolgere questo argomento attraverso un
esperimento ideale: consideriamo un'astronave, nel cui interno si trovi
l'osservatore O'. Nel momento in cui l'astronave passa a velocità v davanti
all'osservatore terrestre O, una sorgente, a bordo dell'astronave, emette un
lampo di luce che viene riflesso da uno specchio. La luce, tornata indietro,
viene assorbita da un rivelatore, posto in prossimità del punto da cui era
stata emessa. L'osservatore nel veicolo spaziale misura allora, con un
proprio orologio, l'intervallo di tempo impiegato dal raggio luminoso per
percorrere il tragitto di andata e ritorno. Per l'osservatore O sulla Terra, la
luce percorre un cammino più lungo rispetto a quello osservato dall'astronauta O'. Poiché la
velocità della luce è c per entrambi, l'intervallo di tempo br valutato da O fra l'emissione e
l'assorbimento della luce è maggiore dell'intervallo bry misurato da O'.
Supponiamo che in K' vi sia un segmento rigido immobile rispetto ad esso ed adagiato
sull'asse delle x. La sua lunghezza rispetto a K' sia ‡y.
Quale sarà la lunghezza l dello stesso segmento rispetto a K ?
Secondo il senso comune e le trasformate di Galileo (che ne sono la forma matematica) la
risposta sarebbe ‡ ‡y, ovvero il segmento viene visto della stessa lunghezza rispetto ad
entrambi i sistemi di riferimento inerziali.
Invece, semplici calcoli applicati alle trasformate di Lorentz portano ad un
risultato sorprendente: l risulta minore di ly secondo la relazione
‡ ‡y‰1 `
p
17
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Solo a velocità prossime a quella della luce si ha una deviazione apprezzabile dal valore ‡y. Se la
velocità di K' tende a c il segmento viene visto da K con una lunghezza sempre minore, tendente
a 0. Se v = c, il segmento diventa (rispetto a K) di lunghezza nulla.
Questi sorprendenti risultati ribadiscono il fatto che a velocità piccole rispetto a c le trasformate
di Lorentz coincidono con le trasformate di Galileo.
Questi fenomeni ci sembrerebbero del tutto normali se entrassero nella nostra esperienza
quotidiana, ciò invece non accade per una ragione molto semplice: questi fenomeni diventano
evidenti quando si viaggia a velocità molto vicine a quelle della luce e tali velocità sono sono fuori
dalla nostra portata. Basta pensare che l’oggetto più veloce che che l’uomo ha costruito può
raggiungere i 20 km/s e la luce è 15 mila volte più veloce. Ma perché avvengono solo in
prossimità della velocità della luce? In realtà essi si producono sempre anche a bassa velocità
ma gli effetti sono troppo piccoli perché ce ne accorgiamo.
Analogia:
Prendiamo un oggetto di metallo e avviciniamolo pian
piano a una calamita. Quando è a 1m l’effetto di
attrazione non si avverte anche se in teoria esiste. Man
mano che ci avviciniamo, questa attrazione si comincia
a sentire e aumenta sempre più fino a che diventa
molto forte e quasi irresistibile.
Per gli effetti relativistici avviene la stessa cosa. Gli
effetti relativistici esistono ma sono inavvertibili, solo se
disponessimo di astronavi capaci di avvicirnarsi alla
velocità della luce entreremmo nel campo degli effetti
molto evidenti.
Massa inerziale e massa gravitazionale
Prima di andare avanti vorrei far notare che nella fase iniziale, quando gli studenti stanno
ancora formando le distinzioni tra i concetti di peso e massa, può essere utile mantenere
una separazione tra le unità di misura, parlando di massa in chilogrammi e di peso in
newton; tuttavia è impossibile difendere gli studenti dall’uso che si può trovare nella
lingua comune: certamente sentiranno dire “un peso di 3 chilogrammi”.
La legge della gravitazione universale descrive quantitativamente l'interazione tra due
masse 9 ed che possiamo considerare puntiformi al variare della distanza tra i loro
centri. Indistintamente possiamo considerare ciascuna delle due masse come esercitante
sull'altra l'azione gravitazionale, in quanto detta azione è perfettamente simmetrica rispetto
alle masse che interagiscono. Studiando i principi della dinamica, la massa è usata per
definire la tendenza di un corpo a mantenere lo stato di quiete o di moto rettilineo ed
uniforme (ossia l'inerzia), mentre ora viene usata ora per rappresentare l'entità
dell'interazione tra due corpi qualsiasi.
Chiariamo il concetto con un esempio:
Supponiamo di voler spingere un blocco di ghiaccio inizialmente fermo su una superficie
orizzontale priva di attrito. Se vogliamo accelerare il blocco ci accorgiamo che occorre
applicare ad esso una forza il cui valore è dato dalla seconda legge di Newton.
In questo caso la gravità non entra in alcun modo nelle nostre considerazioni; anzi possiamo concludere dicendo che anche in uno spazio privo di gravità occorrerebbe sempre la
stessa forza per imprimere al blocco uguale accelerazione. Ciò che rende necessaria una
forza per cambiare lo stato di moto di un corpo viene da noi chiamata massa inerziale m
ed è misurata dal rapporto tra forza F applicata ed accelerazione a prodotta.
Supponiamo ora di tenere lo stesso blocco fermo e sollevato da terra. Chiaramente per
mantenerlo in questa posizione abbiamo bisogno di una forza senza la quale il corpo cadrà
verso terra con moto accelerato. L'intensità di questa forza è data dalla legge della
gravitazione universale ossia:
]1
\ W
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
18
dove m' rappresenta ora la massa gravitazionale.
Per uno stesso corpo abbiamo ora due definizioni di massa. Ciò che ci chiediamo è se m
ed m' siano la stessa cosa.
Consideriamo due corpi A e B di masse gravitazionali Š1 ed ‹1 sotto l'azione di un terzo
corpo C di massa gravitazionale 1 . Supponiamo che C si trovi ad uguale distanza r da A e
da B per cui segue:
Š1 1
‹1 1
Š \
t
\
‹
W
W
II rapporto tra le due forze è:
Š Š1
‹ ‹1
Se supponiamo ora che il corpo C sia la terra si ha Š ŒŠ (peso del corpo A) ‹ Œ‹
(peso del corpo B) da cui
ŒŠ Š1
Œ‹ ‹1
Questo risultato significa che i pesi dei corpi sono direttamente proporzionali alle loro
masse gravitazionali.
Immaginiamo ora di misurare le masse inerziali dei corpi A e B e di trovare mediante
esperimenti di dinamica (come ad esempio quello usato in precedenza per il blocco) che i
loro valori sono Š ed ‹ . Una volta determinati questi valori lasciamo cadere questi corpi
verso terra. Noteremo che nonostante Š sia diverso da ‹ , entrambi i corpi cadranno con
la stessa accelerazione g dovuta all'interazione gravitazionale con la terra ovvero dovuta al
peso. Applicando la seconda legge della dinamica possiamo scrivere ŒŠ Š U t Œ‹ ‹ U.
Ossia:
ŒŠ Š
Œ‹ ‹
Questo significa che i pesi dei corpi sono proporzionali pure alle masse inerziali. Allora
possiamo concludere che massa inerziale e massa gravitazionale sono sicuramente
proporzionali tra loro.
Newton dimostrò con un esperimento da lui progettato che i due tipi di massa non
solo sono proporzionali ma addirittura uguali. L'equivalenza tra massa gravitazionale e
massa inerziale è considerata in fisica classica un fatto del tutto accidentale che non trova
spiegazioni di natura teorica. Al contrario nella fisica moderna, ed in particolare nella
teoria della relatività generale, l'uguaglianza tra massa inerziale e massa gravitazionale
risulta fondamentale per l'interpretazione della gravitazione.
Il principio di equivalenza
La logica concettuale della relatività generale è fondamentalmente espressa dal cosiddetto
principio di equivalenza.
Per illustrare questo principio cominciamo con la constatazione che, poiché la massa
inerziale e la massa gravitazionale sono uguali, tutti i corpi, in un campo gravitazionale
uniforme, cadono con la stessa accelerazione. Perciò, in un laboratorio collocato
all'interno di un campo gravitazionale uniforme, il comportamento degli oggetti materiali è
identico al comportamento degli stessi oggetti quando si trovano, in assenza di gravità, in
un laboratorio sottoposto a un'accelerazione costante. In un dato punto dello spazio, la
gravità e un'opportuna accelerazione del riferimento producono dunque effetti del tutto
equivalenti.
Per giustificare questa affermazione, descriviamo ora uno fra i più famosi esperimenti
mentali einsteiniani.
Esperiemto ideale:
Consideriamo un osservatore dentro un ascensore, sospeso a un cavo e fermo rispetto alla
Terra. Ogni corpo, indipendentemente dalla sua natura, è soggetto alla stessa
19
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
accelerazione di gravità g (fig. 8a). Supponiamo che, a causa della rottura del cavo di
sostegno, l'ascensore precipiti in caduta libera. Durante il volo lo sperimentatore constata
che tutti i corpi, e lui stesso, galleggiano privi di peso (fig. 8b). Trasportato da
un'astronave, immaginiamo poi il nostro ascensore localizzato nello spazio dove i campi
gravitazionali sono trascurabili. Anche in questo caso lo sperimentatore non avverte il
peso degli oggetti, né la reazione del pavimento dell'ascensore sotto i suoi piedi. Egli non
riesce a distinguere questa situazione da quella precedente, nel senso che nessuna
esperienza fatta all'interno dell'ascensore gli permette di capire se sarà destinato a
precipitare al suolo o a galleggiare eternamente nello spazio.
Figura 8. a) In un ascensore immobile rispetto alla Terra ogni corpo è soggetto all'accelerazione di gravita g. b) Se l'ascensore è in caduta
libera i corpi galleggiano privi di peso.
Se, infine, l'ascensore, spinto dai motori dell'astronave, si muove verso l'alto con
un'accelerazione pari, in modulo, all'accelerazione gravitazionale che si avverte sulla
superficie della Terra, l'osservatore stima di trovarsi nelle stesse condizioni illustrate in
figura 8a.
È l'ascensore che sta accelerando nello spazio, o è un effetto gravitazionale?
Nessuna esperienza eseguita dentro l'ascensore può avvalorare una delle due alternative a
scapito dell'altra. Possiamo dunque affermare che, con un opportuno riferimento accelerato, è possibile eliminare o simulare un campo gravitazionale reale. Perciò enunciamo
il principio di equivalenza come segue:
Equivalenza fra un campo gravitazionale e un sistema di riferimento accelerato:
Ogni sistema di riferimento inerziale, immerso in un campo gravitazionale uniforme, è del
tutto equivalente a un sistema di riferimento uniformemente accelerato (rispetto al primo) nel
quale non agisca alcun campo gravitazionale.
Illustrazione sperimentale
L'importanza del fatto che nell’ascensore che cade le cose sono “senza peso” è tale che è
opportuno dare qualche illustrazione sperimentale. Una che si può fare con mezzi
semplicissimi è quello della bottiglia bucata. Si prende una bottiglia di plastica (di acqua
minerale); si riempie d'acqua e si fanno dei forellini sulla parete, vicino al fondo, si
osserva che l'acqua zampilla dai forellini. Ora si lascia cadere la bottiglia, o la si lancia a
un compagno: si constata che durante il volo l'acqua non esce. Dunque quando la
bottiglia è in volo (caduta libera) nel suo rif. la gravità non c'è più.
Riferimenti in caduta libera
Attenzione: quando parliamo di rif. in caduta libera non intendiamo dire solo in moto
verticale (questo è già mostrato dalla bottiglia, che può essere lanciata "a parabola"). In
generale, intendiamo che il rif. si muove sotto l'azione della sola gravità. Il laboratorio può
essere ad es. in orbita attorno alla Terra (satellite artificiale). È per questo che in un
satellite "i corpi sono senza peso"; non perché siamo lontani dalla Terra. C’è in proposito
un errore molto comune fra gli studenti che consiste nel credere che l’apparente assenza
di peso in una stazione spaziale orbitante sia dovuta al fatto che il satellite sia fuori del
20
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
campo gravitazionale terrestre; a questo si può fare obiezione: il campo si estende anche
molto lontano dalla Terra, com'è provato, tra l'altro, dal moto della Luna.
Analogia
La situazione dell’astronauta all’interno della navicella spaziale è del tutto analoga a
quella di un osservatore che si trova all’interno dell’ascensore in caduta libera.
Un modo equivalente di formulare il principio di relatività di Einstein è affermare che la
massa inerziale e la massa gravitazionale sono equivalenti. Se ci fosse la possibilità
operativa di distinguere le due masse, si potrebbe infatti riconoscere un sistema
accelerato in assenza di gravità da un sistema inerziale immerso in un campo
gravitazionale. Notiamo inoltre che, poiché l'universo fisico descritto da un riferimento
accelerato è equivalente a un universo soggetto a un campo gravitazionale, la teoria della
relatività generale è al tempo stesso una teoria della gravità.
Nota didattica
Vorrei sottolineare che per seguire Einstein nel suo ragionamento bisogna imparare a fare
una certa ginnastica mentale: vedere cose vecchie in modo nuovo. Il che non implica
ancora necessariamente di vedere cose nuove; ci sono anche queste, ma prima bisogna
imparare a rivedere le cose che ci sono familiari, interpretandole in un modo diverso.
Conseguenze del PE - Effetto della gravità sulla luce
Dopo aver formulato il PE, per comprenderne il significato fisico occorre esplorarne le
conseguenze sperimentalmente verificabili. L’importanza del PE sta infatti in primo luogo nel
gran numero di previsioni originali e sorprendenti che discendono.
Esperiemto ideale:
Una notevole conseguenza del principio di equivalenza riguarda la
propagazione della luce, come suggerito dall'esperimento mentale illustrato in figura 9. Facciamo nuovamente l'ipotesi che una cabina di
ascensore sia trasportata da un'astronave, insieme all'ignaro
passeggero chiuso al suo interno, in un punto dello spazio in cui il
campo gravitazionale sia trascurabile. Supponiamo inoltre che l'uomo,
mentre la cabina è in moto accelerato verso l'alto, invii un lampo
luminoso in direzione orizzontale verso la parete destra.
Durante il tempo in cui la luce si propaga, la cabina accelera; di conseguenza il punto in cui la luce colpisce la parete si trova a un'altezza
minore, rispetto al pavimento, del punto dal quale il lampo è partito.
Nel sistema accelerato dell'ascensore, la traiettoria della luce risulta
dunque piegata verso il basso. Per il principio di equivalenza, in un
ascensore fermo sulla Terra, soggetto alla forza di gravità, il fascio di luce deve essere ugualmente
piegato verso il basso dal campo gravitazionale.
Fisica e geometria
La relatività generale è essenzialmente una teoria geometrica, nella teoria di Einstein, la
materia curva lo spazio e l'effetto di una massa su un'altra è rappresentato dal moto della
seconda massa nella geometria distorta dalla prima. La figura 10 mostra un'analogia
bidimensionale per la curvatura dello spazio. Si immagini un foglio di gomma con un sistema
di coordinate a griglia steso su esso. Tutto il moto è confinato nel sistema di coordinate steso
sul foglio. Si immagini ora una palla che provoca sul foglio un avvallamento, deformando così
il foglio. La minima distanza tra due punti non è più un segmento di retta; di fatto, nella
nuova geometria, bisogna ridefinire con precisione che cosa si intende con il termine «linea
retta».
21
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis
Vi sono delle situazioni sperimentali molto famose che hanno permesso la verifica diretta delle
conseguenze e della validità della teoria della relatività generale.
La precessione del perielio di Mercurio:
Questo comportamento "strano" di Mercurio fu spiegato da
Einstein come conseguenza delle sue equazioni, appena
trovate, e senza bisogno di nessuna ipotesi addizionale. Purtroppo una spiegazione del modo come la precessione risulta
dalla RG è decisamente al di fuori delle possibilità di una
presentazione elementare, quindi dobbiamo rinunciare a
descriverla. Questo non vuoi dire però che l'argomento debba
essere ignorato: al contrario, si tratta di un esempio
straordinario per capire che cos'è una teoria scientifica e il
suo potere predittivo. Einstein non costruì la RG per spiegare
il moto di Mercurio: seguì una linea di ragionamento del tutto
diversa. Ma una volta arrivato alle equazioni che collegavano
la massa del Sole e la curvatura dello spazio-tempo nel suo
intorno, quel comportamento di Mercurio ne seguiva con
inderogabile necessità!
La deflessione dei raggi luminosi
Probabilmente la più famosa verifica della della teoria è la
deflessione della luce stellare in prossimità del Sole che fu
fatta nel 1919 in occasione di una eclissi totale di sole:
grazie ad essa è possibile osservare la deviazione apparente di
Figura 10 a) La “rete nello spazio” è
stelle molto vicine al bordo del disco solare.
un'immagine in due dimensioni
Il 29 maggio del 1919, durante un eclissi di sole e quindi con
della
geometria
tridimensionale
una netta o quasi completa diminuzione dell’irraggiamento
dello spazio ordinario. In assenza di
solare, alcuni illustri astronomi inglesi riuscirono a
masse esso segue la geometria
fotografare e poi a calcolare la posizione di queste stelle.
euclidea. b) La presenza di un
Sapendo la posizione reale, che è stata calcolata mesi prima
oggetto massiccio produce una
(o dopo) l’eclissi quando il Sole era dalla parte opposta e
“deformazione” della rete dello
quindi quando la deviazione dei raggi luminosi, causato dal
spazio, creando una sorta di buca.
campo gravitazionale di quest’ultimo, era trascurabile; è stato
Gli altri oggetti che si muovono
possibile calcolare l’angolo con cui i raggi sono stati deviati. I
nelle vicinanze subiranno pertanto
delle perturbazioni nel loro moto,
dati ricavati dall’esperienza si accordavano, ovviamente con
tanto più forti quanto più si
un leggero margine di errore, con quelli predetti dalla teoria
avvicinano all'oggetto causa della
della relatività generale.
deformazione.
Secondo quanto stabilito dalla teoria della relatività, la luce
rappresenta il più rapido segnale che può congiungere due posizioni A e B: il percorso spaziotemporale compiuto dalla luce per andare da A a B costituisce dunque un tratto di geodetica
spazio-temporale (è questa infatti la definizione di geodetica). Poiché tale percorso, in
presenza di campo gravitazionale, è curvo, possiamo dire che il campo gravitazionale incurva
lo spazio.
La geometria sferica (necessaria per descrìvere ad
esempio il moto di un oggetto sulla superficie
terrestre, su cui le geodetiche sono archi di cerchio) è
una geometria non euclidea. Analogamente, in
relatività generale è non euclidea la geometria dello
spazio-tempo.
Nota didattica
Nella scuola secondaria superiore la deflessione gravitazionale della luce può essere affrontata
piuttosto presto: è un fatto abbastanza elementare che non presenta punti critici. È
sufficiente che gli allievi abbiano capito il principio di equivalenza.
22
Portfolio – La legge di Gravitazione universale | Angela Maria De Santis