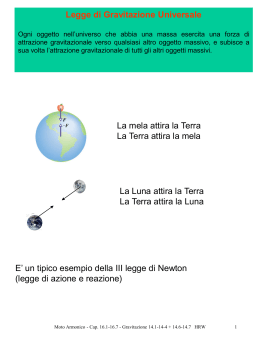
Anno 2008/2009
Classe IV E
Gagliardi Gabriele, Marchi Lorenza,
Rossi Maddalena, Valmarin Sergio,
Voltini Giulia
La Leggenda
 Caduta della mela dall’albero:
 Se la mela fosse caduta da
un’altezza pari alla distanza
tra la Luna e la Terra?
 Teorie di Platone e Aristotele
 Teorie di Keplero
 Conclusione di Newton
Isaac Newton
(1642-1727)




Filosofo, matematico, fisico e
alchimista inglese
Dimostrò che le leggi della natura
governano il movimento della terra e
degli altri corpi celesti
Rivoluzione scientifica e teoria
eliocentrica
Sistematizzazione matematica delle
leggi di Keplero
La deduzione newtoniana della legge di
gravitazione Universale

Newton scoprì che le masse dei corpi
celesti si attraggono con una forza
direttamente
proporzionale
al
prodotto delle masse e inversamente
proporzionale
al
quadrato
delle
distanze; tale attrazione prese il nome
di gravità.
1 2
2
mm
F G
R
Come Newton giunge alla legge di Gravitazione
Universale

Sapendo che nel moto circolare
uniforme l’accelerazione centripeta è
v2
ac 
 2R
R
e che
2

T
4
ac  2 R
T
2
Terza Legge di Keplero
3
R
R  kT  T 
k
3
2
2
3
18
2
m
Dove k = 3
,
38

10
s
Sostituiamo
T
2
4
ac  2 R
T
2
nella formula
4
4
ac  3 kR  2 k
R
R
2
2
4 k
2
è una costante quindi posto
4 k  C S
2
ricaviamo che:
CS
ac  2
R
Tenendo conto della II Legge della dinamica F = ma
andando a sostituire l’accelerazione centripeta, si
potrà affermare che sul pianeta P esiste una forza
orientata verso il Sole:
FSP
mP C S
 mP a 
2
RSP
ma Newton mirava a una espressione universale della forza
agente fra i corpi
FPS
principio di
azione e reazione
mS C P

2
RPS
Le due forze appena espresse devono
essere uguali
FSP  FPS
Sostituendo ad
FSP
e ad
e semplificando
il temine comune
R
FPS
le loro espressioni
m P C S mS C P
 2
2
RSP
RPS
2
PS
mS C P  m P C S
Da cui dividendo entrambi i membri per l’equazione
per
mS mP
:
CS CP

mS m P
 Questo procedimento si può ripetere
per tutti i pianeti del Sistema Solare
 Allora il rapporto fra la costante C m di
un generico centro attrattore e la sua
massa risulta uguale per qualunque
corpo
considerato
come
centro
dell’attrazione
e
rappresenti
la
costante G, che è la costante di
Gravitazione Universale.
C S C P Cm
G


mS m P
m
 Tornando alle forze FSP - F
possiamo
PS
ora sostituire in entrambe la costante G
ricordando che C  Gm
P
P
e C S  GmS
Così otteniamo:
FSP
mS mP
G 2
RSP
FPS
mP mS
G 2
RPS
 Siccome le formule sono identiche la legge
si può definire valente per qualsiasi coppia
di corpi nell’Universo
Gravitazione Universale
m1m2
F G 2
R
Legge di
CONSIDERAZIONI SULLA LEGGE DI
GRAVITAZIONE UNIVERSALE
Unificazione di Terra e Cielo

La deduzione di Newton è valida
per qualsiasi massa, celeste o
terrestre,
quindi
è
in
contrapposizione con la concezione
filosofica greca.
IL PROBLEMA DELLA NATURA DELLA
FORZA GRAVITAZIONALE
Newton
si
rifiuta
di
spiegare
l’attrazione
fra
due
corpi
con
l’esistenza dell’”attrattività”
 Grazie alle ultime scoperte possiamo
affermare che ogni forza, anche quella
Gravitazionale, si sviluppa in un
campo in virtù di un mediatore, in
questo caso il gravitone

La gravitazione: una forza
fondamentale




Forza
Forza
Forza
Forza
gravitazionale
nucleare debole
elettromagnetica
nucleare forte
MASSA INERZIALE e MASSA
GRAVITAZIONALE
Fino al 1600 la massa corrisponde
all’inerzia → massa inerziale
Dopo
Newton
e
la
legge
di
gravitazione la massa corrisponde alla
capacità di un corpo di attrarre e
essere attratto da altri corpi → massa
gravitazionale
Definiamo:
mi la massa inerziale
m g la massa gravitazionale
Considerando la seconda legge
della dinamica e l’espressione
del peso di un oggetto:
F  mi a
P  mg g
mi e m g hanno lo stesso valore?
Se i valori fossero
diversi la legge del
pendolo
cambierebbe.
Infatti si avrebbe:
F//  mi a
P  m g g
E per la similitudine dei
triangoli:
F// : P  x : l  F// l  Px
E sostituendo:
mi al  mg gx  a  
mg g
mi l
x
Confrontando con la legge:
ax
2
Si riconosce che si tratta di un
moto oscillatorio:
m
g
g
2

m
l
i
Da cui:


m
g
g
m
l
i
Ricordando che:
2

T
Si ha:
2

mi l
T
mg g
Da cui:
mi l
T  2
mg g
 Pendoli della stessa lunghezza,
costituiti da corpi aventi lo stesso
peso, cioè m g , ma mi diversa,
oscillerebbero con periodi diversi.
m g = mi
 Anche Newton stesso verificò
, postulato base della teoria della
relatività generale di Einstein

Conclusioni
► Massa
inerziale massa gravitazionale
sono due termini diversi per indicare
due
proprietà
identificate
in
fenomeni diversi, ma riconducibili ad
un unico concetto di massa.
IL VALORE DELLA COSTANTE G
Esperimento di Cavendish


1771:
Henry
Cavendish,
esperimento valore G.
Usò: bilancia di torsione per
misurare forza di attrazione
gravitazionale tra masse note m
e M.

Le sfere grandi di
massa M attirano la
sferette più vicina
con
una
forza
gravitazionale F
coppia di forze che
provoca
una
rotazione dell’asta
(α)

La rotazione raggiunge
l’equilibrio quando la
reazione con cui il filo si
oppone alla torsione
uguaglia l’azione
gravitazionale fra le masse


La resistenza del filo alla torsione
è proporzionale all’angolo di
direzione α.
Dalla
misura
dell’angolo
di
torsione si può risalire al
momento torcente del filo e alla
forza F.
Considerazioni:

Detta r la distanza fra il centro della
sfera piccola (m) e quello della sfera
grande (M) alla quale si è avvicinata.
Dalla legge di gravitazione universale
si ha:
mM
F G 2
r
da cui
2
Fr
G
mM

Newton aveva dimostrato che la
legge di gravitazione universale vale
anche se uno dei corpi può essere
considerato
puntiforme
all’altro che è sferica
rispetto

Con la bilancia torsione di Cavendish si riesce ad
ottenere il valore G, detto Costante di
Cavendish:
G  6,67 10
11
2
Nm / kg
2
La costanza dell’accelerazione di gravità
in prossimità della superficie terrestre

L’applicazione della legge di gravitazione
porta a:
MT
g  G 2  9,8m / s 2
RT

Il valore g in prossimità della superficie
terrestre non dipende dalla massa del corpo
tutti i corpi in prossimità della
superficie terrestre cadono con la stessa
accelerazione

Accelerazione
sulla Luna
MT
aL  G 2
RTL
 Tenendo
conto del fatto che in questo
caso il raggio orbitale della Luna è 60
volte quello terrestre
 Quindi il rapporto tra le due
accelerazioni è:
2
R
g
TL


3
2
a
R
L
T
La massa della Terra
• Conoscendo la costante di Cavendish G e il
valore sperimentale g
g
9
,
8
m
/
s
(
6
,
4

1
m
)
M



6

1
K
G
6
,
6

1
N
/
K
2
2
6
2
2
T
T

1
2
2
• Il valore ottenuto è quasi doppio di quello
stimato da Newton, non avendo tenuto della
composizione interna della Terra.
La massa del Sole

Noto il periodo T di rivoluzione della
7
3
,
16

10
s
)
Terra intorno al Sole (
e il raggio RTS
1
,
5

10
m
)l’accelerazione
della sua orbita (
centripeta aC della Terra risulta data da:
11
2
(
a


R
)
c

2
TS
2
4
R
a

c
T
 La
forza che fa ruotare la Terra intorno
al Sole è allora:
4 mT RTS
FC  mT aC 
2
T
2
 Che
può anche essere espressa così:
M S mT
FC  G
2
RTS
 Uguagliando
allora i termini di destra
delle equazioni delle forze centripete
si ottiene:
4 R
4 (1,5 10 m)
30
MS 

 2 10 Kg
11
2
2
7 2
GT
6,67 10 Nm / Kg (3,16 10 s)
2
2
TS
2
2
11
3
La massa dei pianeti
 In
questo modo si può calcolare la
massa di un qualsiasi pianeta dotato
di un satellite
 In assenza di esso, si utilizza il
metodo delle perturbazioni
La costante di Keplero
E’ relativa al centro attrattore M C e un
suo qualunque satellite di massa m S
M
m
4

CS
G2 
m
R
S 2 CS
R
T
CS
2
► Semplificando
riscrivere:
e riordinando possiamo
2
CSC
2
2 C

RM

G

k
T4
► Nel

caso del sistema Terra – Sole si
ottiene:
N
2

1
K
m
k

6
,
6

1

3
,
3

1
K
4
s
2
3
3

1
1
S
2
2
2
PERIODO DI ROTAZIONE DI
UN SATELLITE ARTIFICIALE


Intorno alla Terra ruotano migliaia di
Satelliti e ne possiamo calcolare il
periodo di rotazione quando questi
seguono un’orbita circolare
Impostiamo la relazione:
M T mS
4
G

m
R
S
TS
2
2
RTS
T
2
Da ciò si ha:
4 R
R
T 
 T  2
GM T
GM T
2
2
3
TS
3
TS

Sostituendo i valori numerici:
(6,9 10 m)
T  2

11
2
2
24
6,67 10 Nm / Kg 6 10 Kg
6
 5,69 10 s  95 min
3
3