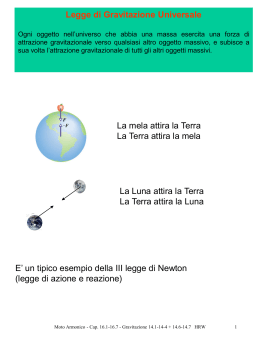
Leggi di Keplero Gravitazione Gravitazione Prima legge: I pianeti percorrono orbite ellittiche intorno al sole che occupa uno dei fuochi dell’ellisse Seconda legge: La velocità areale con cui il raggio vettore che unisce il sole ad un pianeta descrive l’orbita è costante Terza legge: Politecnico di Bari Ingegneria Elettrica Il quadrato del periodo di rivoluzione di ogni pianeta è proporzionale al cubo del semiasse maggiore dell’ellisse: T 2 = kr 3 Corso di Fisica Sperimentale I Prof. G. Iaselli 1 Forza gravitazionale Gravitazione Gravitazione Ipotizzando orbite circolari, se la velocità areale è costante il moto di un pianeta è circolare uniforme 1 2d d θ A= r 2 dt dt se A ed r sono costantiθ è costante La forza che agisce sul pianeta, permettendogli di percorrere una traiettoria circolare con velocità costante deve essere esclusivamente centripeta F = mω 2 r 2 2π 2 π ⎛ ⎞ ⇒ F = mω 2 r = m⎜ ⎟ r ma ricordando ω = T ⎝T ⎠ T= periodo di rivoluzione m= massa pianeta r= raggio dell’orbita del pianeta Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 2 Forza gravitazionale Gravitazione Gravitazione Utilizzando la terza legge di Keplero T 2 = kr 3 confondendo il raggio della circonferenza con il semiasse maggiore dell’ellisse, la forza sarà: 4π 2 m F= k r2 La forza esercitata dal Sole sui pianeti è inversamente proporzionale al quadrato della distanza dal Sole Consideriamo il sistema Sole-Terra: 4π 2 mT la forza esercitata dal Sole sulla Terra: FS ,T = kT r 2 la forza esercitata dalla Terra sul Sole: FT , S Politecnico di Bari Ingegneria Elettrica 4π 2 mS = kS r 2 Corso di Fisica Sperimentale I Prof. G. Iaselli 3 Forza gravitazionale Gravitazione Gravitazione per il principio di azione e reazione le due forze sono uguali in modulo da cui: mT k S = mS kT 4π 2 4π 2 = Definendo la costante γ = mT k S mS kT possiamo scrivere per il modulo della forza Sole-Terra: FS ,T = γ mS mT r2 Legge di gravitazione universale: date due masse qualsiasi, di dimensioni trascurabili rispetto alla mutua distanza, tra di esse agisce una forza attrattiva diretta lungo la retta congiungente le due masse, il cui modulo dipende direttamente dal prodotto delle masse e inversamente dal quadrato della distanza. Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 4 Forza gravitazionale Gravitazione Gravitazione γ costante universale In termini vettoriali la forza gravitazionale: F1, 2 = −γ m1 m2 r 2 û1, 2 Prima verifica, ad opera di Newton: corpo di massa m posto sulla Terra (massa mT e raggio rT ) F =γ ma F = mg ⇒ g = γ mT mT m rT2 rT2 per il sistema Terra-Luna: FT , L = γ da cui γ mT = ω L2 rL3 mT mL rL2 = mLω L2 rL dal periodo di rotazione della Luna attorno alla Terra e dalla distanza Terra-Luna si può calcolare il prodotto γ mT e quindi g Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 5 Forza gravitazionale Gravitazione Gravitazione Misura diretta di γ , ad opera di Cavendish: per mezzo di una bilancia di torsione misurò la forza di attrazione tra due masse sferiche F1, 2 = −γ γ = 6.67 ⋅10 −11 m3 kg s 2 m1 m2 r 2 û1, 2 mT = 5.98 ⋅1024 kg solo conoscendo γ si possono determinare le masse dei corpi celesti Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 6 Energia potenziale gravitazionale Gravitazione Gravitazione Abbiamo dimostrato che Ug = − Inoltre per una particella in moto circolare uniforme 1 E = mv 2 + U g 2 mv 2 GmM = 2 r r ricordando che ⇒ GmM r 1 GmM E=− 2 r2 Energia totale negativa ! Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 7 Gravitazione Gravitazione Energia totale gravitazionale (E<0) E r E Ug Con l’energia cinetica disponibile ci si può arrivare sino ad r Ec Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 8 Energia totale gravitazionale (E=0) Gravitazione Gravitazione E E Ec Ug Politecnico di Bari Ingegneria Elettrica r In questo caso l’energia cinetica disponibile è sufficiente per arrivare ad r=∞ Corso di Fisica Sperimentale I Prof. G. Iaselli 9 Energia totale gravitazionale (E>0) Gravitazione Gravitazione E E Ec r Il corpo può arrivare ad r=∞ ed ha ancora energia per continuare il moto Ug Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 10 Orbite Gravitazione Gravitazione r vo E>0 h E=0 R E<0 Per mettere in orbita un corpo è necessario anche che L≠0 a seconda dell’energia totale si avranno diversi tipi di orbite GmM 1 E = mv02 + 2 R+h Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 11 E le orbite? Gravitazione Gravitazione dipende solo da r 1 2 E = Ec + U (r ) = mv + U (r ) 2 (forza centrale) Ricordiamo che r vr ûr r vϑ ϑ d r d v = r uˆr + r ϑ uˆϑ dt dt r d v = r uˆr + ωr uˆϑ dt ûϑ r 2 ⎛d ⎞ ⎛d ⎞ Allora v 2 = vr2 + vϑ2 = ⎜ r ⎟ + r 2 ⎜ ϑ ⎟ ⎝ dt ⎠ ⎝ dt ⎠ Politecnico di Bari Ingegneria Elettrica 2 Corso di Fisica Sperimentale I Prof. G. Iaselli 12 Orbite Gravitazione Gravitazione Abbiamo dimostrato che 2 ⎛d ⎞ ⎛d ⎞ v2 = ⎜ r ⎟ + r 2 ⎜ ϑ ⎟ ⎝ dt ⎠ ⎝ dt ⎠ 2 Ricordiamo la definizione di momento angolare r r r r r r L = r ∧ p = r ∧ m(vr + vϑ ) r r d r r r L=rmr ϑ L = r ∧ mvr + r ∧ mvϑ dt =0 d ϑ L=mr dt 2 Poiché la forza è centrale L = costante Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 13 Orbite Gravitazione Gravitazione 2 2 d d L ⎞ ⎛ L = m r2 ϑ ⇒ r2⎜ ϑ ⎟ = dt ⎝ dt ⎠ (mr )2 2 2 2 L2 2 ⎛d ⎞ 2⎛ d ⎞ 2 ⎛d ⎞ v = ⎜ r⎟ + r ⎜ ϑ⎟ ⇒ v = ⎜ r⎟ + ⎝ dt ⎠ ⎝ dt ⎠ ⎝ dt ⎠ (mr )2 Quindi l’energia totale è 1 2 E = mv + U g 2 Politecnico di Bari Ingegneria Elettrica 2 L2 1 ⎛d ⎞ E = m⎜ r ⎟ + +Ug 2 2 ⎝ dt ⎠ 2mv Corso di Fisica Sperimentale I Prof. G. Iaselli 14 Orbite Gravitazione Gravitazione 2 1 ⎛d ⎞ L2 E = m⎜ r ⎟ + +Ug 2 2 ⎝ dt ⎠ 2mv energia cinetica per il moto radiale L2 2mv 2 energia potenziale + U g = U eff energia potenziale effettiva 2 1 ⎛d ⎞ E = m⎜ r ⎟ + U eff (r ) 2 ⎝ dt ⎠ Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 15 Orbite Gravitazione Gravitazione soluzione del problema del moto 2 1 ⎛d ⎞ E = m⎜ r ⎟ + U eff (r ) 2 ⎝ dt ⎠ E = costante 1 ⎫2 [ ] d ⎧2 r = ⎨ E − U eff ⎬ dt ⎩m ⎭ r ∫ t dr 1 ⎤2 ⎢⎣ m (E − U eff )⎥⎦ 0⎡2 Politecnico di Bari Ingegneria Elettrica = ∫ dt 0 la soluzione da r in funzione del tempo Corso di Fisica Sperimentale I Prof. G. Iaselli 16 Orbite Gravitazione Gravitazione inoltre L d ϑ= 2 dt mr ϑ t ∫ dϑ = ∫ 0 L 0 mr 2 dt la soluzione da θ in funzione del tempo se mettiamo insieme le due equazioni precedenti troviamo l’equazione della traiettoria r ↔ϑ Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 17 Orbite Gravitazione Gravitazione si dimostra che E<0 orbite ellittiche E=0 orbite iperboliche E>0 orbite paraboliche Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 18 Orbite chiuse Gravitazione Gravitazione a semiasse maggiore dell’ellisse m M a ε eccentricità 0< ε<1 (ε =0→circonferenza) E=− 2a GmM 2a 2E ⎛ L ⎞ 2 ε = 1+ ⎜ ⎟ m ⎝ GmM ⎠ 2a l’energia determina a 2 l’eccentricità dipende da E e da L 2a orbite con la stessa energia ma con L differente Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 19 Potenziale efficace Gravitazione Gravitazione 2 E U eff = L 2mr 2 L2 2mr − 2 GmM r U eff r − GmM r Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 20 Potenziale efficace Gravitazione Gravitazione E r1 r2 orbita chiusa r l’orbita è delimitata tra r1 ed r2 E Ec Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 21 Potenziale efficace Gravitazione Gravitazione E E orbita aperta r Politecnico di Bari Ingegneria Elettrica r la particella arriva dall’infinito, passa da r e poi torna indietro Corso di Fisica Sperimentale I Prof. G. Iaselli 22 Potenziale efficace Gravitazione Gravitazione E orbita chiusa r moto circolare r=costante E Politecnico di Bari Ingegneria Elettrica Corso di Fisica Sperimentale I Prof. G. Iaselli 23
Scaricare