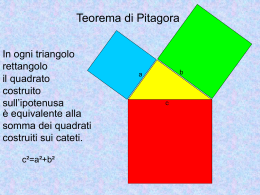
Corso per socializzare le
Indicazioni
settembre 2007
Castellaneta – I.P.S “Perrone”
Indicazioni 2007 per un curriculum verticale – unitario – interdisciplinare
Insegnamento per un apprendimento “divergente”
(parte b)
Suggerimenti per gli insegnanti
della scuola dell’infanzia

Sviluppare la competenza significa
tendere verso un crescente livello di
padronanza della capacità di
trasferire le esperienze e i saperi in
campi diversi da quelli appresi e in
tutti i contesti della vita quotidiana.
Riflessioni o Raccomandazioni!
L’apprendimento
avviene attraverso l’esperienza,
l’esplorazione,


…scoprire e vivere il proprio tempo
esistenziale senza accelerazioni
e senza rallentamenti indotti dagli
adulti.
Ancora suggerimenti per gli
insegnanti della scuola primaria


Gli insegnanti predispongono occasioni di
apprendimento orientate e strutturanti per
favorire nei bambini l’organizzazione di ciò
che vanno scoprendo.
…opportunamente guidati ad approfondire
e sistematizzare gli apprendimenti ed
avviare, processi di simbolizzazione e
formalizzazione.
Suggerimenti sui Metodi per il
concetto di misura e numero
La riflessione sulla quantità e sul
numero scaturisce da situazioni di
vita quotidiana, dal gioco..
…. dall’interagire con lo spazio in modo
consapevole e dal compiere i primi
tentativi per rappresentarlo;
avvicinarsi al numero come segno e
strumento per interpretare la realtà e
interagire con essa;

Cosa deve saper fare










Il bambino sa raggruppare e ordinare secondo criteri diversi, confrontare e
valutare quantità; utilizza semplici simboli per registrare; compie
misurazioni utilizzando semplici strumenti.
Sa collocare correttamente se stesso, oggetti, persone nello spazio.
Segue correttamente un percorso sulla base di indicazioni verbali.
Dimostra di sapersi orientare nell’ organizzazione cronologica della
giornata scolastica.
Riferisce eventi del passato recente dimostrando consapevolezza della loro
collocazione temporale e sa formulare correttamente riflessioni e
considerazioni relative al futuro immediato e prossimo.
Conosce i giorni della settimana, le ore della giornata e sa orientarsi nel
tempo della vita quotidiana e cogliere le trasformazioni naturali.
Il bambino ha imparato ad osservare sulla base di criteri o ipotesi, con
attenzione e sistematicità.
Si dimostra curioso, esplorativo, pone domande, discute, confronta ipotesi,
spiegazioni, soluzioni e azioni.
È in grado di prendersi cura di piante e piccoli animali.
Utilizza un linguaggio appropriato per descrivere le osservazioni o le
esperienze.
Formazione permanente


Più solide saranno le strumentalità
apprese nella scuola primaria,
maggiori saranno le probabilità di
inclusione sociale e culturale
attraverso il sistema dell’istruzione.
La scuola secondaria di primo grado
rappresenta la fase in cui si realizza
l’accesso alle discipline come punti di
vista sulla
Il passaggio all’apprendimento
disciplinare nella scuola secondaria
di primo grado

I problemi complessi richiedono, per
essere esplorati, che i diversi punti di
vista
disciplinari
interessati
dialoghino prestando attenzione alle
zone di confine e di cerniera tra le
discipline.
Metodo del problem solving

La comprensione di specifici temi e
problemi, infatti, non si realizza
soltanto con l’introduzione ai quadri
teorici
e
metodologici
propri
di
ciascuna disciplina, ma anche mediante
approcci integrati, atti a meglio
focalizzare la complessità del reale e a
promuovere modalità di elaborazione
progressivamente più complesse.
Competenze per vivere

Le competenze sviluppate nell’ambito
delle singole discipline concorrono a loro
volta alla promozione di competenze più
ampie e trasversali, che rappresentano
una condizione essenziale per la piena
realizzazione personale e per la
partecipazione attiva alla vita sociale
Il motore del pensiero rfazionale

Favorire l’esplorazione e la scoperta, al fine di promuovere
la passione per la ricerca di nuove conoscenze.
In questa prospettiva, la problematizzazione svolge una
funzione insostituibile:
sollecita gli alunni ad individuare problemi, a sollevare
domande, a mettere in discussione le mappe cognitive già
elaborate, a trovare piste d’indagine adeguate ai problemi,
a cercare soluzioni anche originali in direzione del pensiero
divergente e creativo.
.
Metodologia laboratoriale

Realizzare percorsi in forma di
laboratorio, per favorire l’operatività
e allo stesso tempo il dialogo e
la riflessione su quello che si fa. Il
laboratorio è una modalità di lavoro
che incoraggia la sperimentazione e
la progettualità, coinvolge gli alunni
nel pensare-realizzare-valutare
Saper leggere e scrivere

L'obiettivo primario (che non esclude il
raggiungimento di traguardi più complessi,
sempre possibili) sarà quello di portare gli
allievi a scrivere in modo chiaro, preciso e
semplice;
gli
allievi
dovrebbero
poter
controllare, oltre alle scelte lessicali e
sintattiche,
anche
gli
elementi
relativi
all'organizzazione logico-concettuale del testo,
e quindi sviluppare la capacità di ordinare,
raggruppare, esplicitare tutte le informazioni
necessarie al raggiungimento dello scopo
obiettivi dell’area linguistica
Lingua e logica

L’uso della lingua è espressione delle
facoltà intellettive e aiuterà l’alunno
a rendere rigoroso il suo pensiero. In
questa prospettiva metacognitiva,
anche la riflessione sulla lingua
servirà per sviluppare le capacità di
categorizzare, di connettere, di
analizzare.
Saper comprendere attraverso la
lingua


Seguire istruzioni scritte per
realizzare prodotti, per regolare
comportamenti, per svolgere
un'attività, per realizzare un
procedimento.
Comprendere e utilizzare il significato
di parole e termini specifici legati alle
discipline di studio
Competenze nell’area linguistica
Competenze linguistiche trasversali

Nelle attività di studio, personali e
collaborative, usa i manuali delle
discipline o altri testi di studio,
al fine di ricercare, raccogliere e
rielaborare i dati, le informazioni, i
concetti e le esperienze necessarie,
anche con l’utilizzo di strumenti
informatici.
Competenze matematicoscientifico-tecnologiche
Ad ogni livello scolastico, il risolvere problemi,
anche con strumenti e risorse digitali, offre
occasioni per acquisire nuovi concetti ed abilità, per
arricchire il significato di concetti già appresi e
per verificare l’operatività degli apprendimenti
realizzati in precedenza.
 Componenti
necessarie di questo comune
approccio sono l’impostare e il risolvere problemi,
la capacità di costruire storie e schemi
interpretativi e di sviluppare argomentazioni,
l’affinare il linguaggio naturale e la capacità di
organizzare il discorso, con una speciale
attenzione all’uso della lingua, in particolare della
lingua italiana.

Conclusioni


La costruzione del pensiero matematico è un processo
lungo e progressivo nel quale concetti, abilità, competenze
ed atteggiamenti vengono ritrovati, intrecciati, consolidati e
sviluppati a più riprese; è un processo che comporta anche
difficoltà linguistiche e che richiede un’acquisizione graduale
del linguaggio matematico.
Per questo motivo i traguardi per la terza classe della
scuola secondaria di primo grado sono presentati come
un’evoluzione di quelli per la quinta classe della scuola
primaria e gli obiettivi per ciascun livello comprendono in
ogni caso anche quelli del livello precedente, naturalmente
intesi con un grado maggiore di complessità delle situazioni
considerate e di padronanza da parte dell’alunno.
curriculum di
matematica deve essere
un curriculum
“praticabile
Pensiero convergente e divergente
Link



Questa distinzione fra le due forme di
pensiero si deve a Guilford.
La memoria fa convergere verso
un’unica soluzione (apprendimento
nozionistico)
La creatività fa divergere verso più
soluzioni originali ed efficaci quando
si affrontano problemi reali.
Inventiamo una storiella per
giocare a cercare possibili
combinazioni, disposizioni …..
Da un po’ di tempo i conigli si
dimostravano un investimento
vantaggioso e così un allevatore
intraprendente aveva preparato otto
gabbie, per ciascuna delle quali avrebbe
disposto una coppia di conigli. La notte
prima di andare al mercato qualcuno gli
rubò una gabbia, ma l’ingegnoso
allevatore riuscì a portare al mercato le
otto coppie di conigli
Esaminare le soluzioni trovate dai
bambini



Invitare ad osservare sulla quantità
di lati utilizzati
Numerare le situazioni in cui non
sono utilizzati tutti
Affermare che non è possibile creare
più di un quadrato con cinque e
proporre la soluzione con sette




Invitare gli alunni a creare quadrati
con un numero di variabile di
bastoncini
Esaminare le loro costruzioni
Far contare il numero di elementi
utilizzati
(possibili combinazioni link)
Se non sono arrivati all’idea di
affiancare i quadrati

Proporre di formare due quadrati
togliendo uno da otto bastoncini
Invitare gli alunni a cercare
contenitori per scoprire come sono
realizzati
Quali altri nodi concettuali
matematici si realizzano cercando
combinazioni possibili con questo
gioco?




Equicomposizione
Modulo
Misura
Legge matematica
Trasposizione didattica
“aree senza confini”
Far osservare che
 con quattro elementi si può realizzare un
modulo
 con un numero minimo di elementi si
possono realizzare superfici equivalenti
formate dallo stesso numero di moduli.
Invitare gli alunni
aumentando il numero di elementi a
creare superfici equivalenti di forma
diversa
Questa attività determinerà in modo
naturale relazioni tra perimetro e
superfici.
Invitiamo alla ricerca





Si potrebbe chiedere su ogni
combinazione realizzata:
Quanti moduli?
Quanti elementi esterni per formare
il contorno?
Quanti elementi interni non
appartengono al perimetro?
Quante partizioni ha la figura?
Metodo di Eudosso-Archimede Cavalieri
Concetto di tassellatura
Pavimentazione isometrica e non
Schematizziamo utilizzando tabelle per una
possibile distribuzione degli elementi
Numero di Perimetro
quadrati
1
4 u = (1+3)u
2
3
4
7 u = (4+3)u
10 u = (7+3)u
13 u = (10+3)u
Per un’altra distribuzione
2 = 2*1
6= 3*2
4=2*2
8= 4*2
6=2*3
10=5*2
Soluzione ottimale

Otto gabbie affiancate a due a due








Con
Con
Con
Con
Con
Con
Con
Con
1 quadrato è possibile una disposizione
2 quadrati si può fare una disposizione
3 quadrati è possibile fare una disposizione
4 quadrati si hanno due tipi di disposizioni
5 quadrati …..
6…..
7…..
8…..



.
.
Con quali perimetri per ciascuna disposizione?
Quale soluzione determina il minimo perimetro?
Ancora una trasposizione didattica
Un quadrato magico si costruisce
disponendo tutti i numeri interi da in
una griglia di n*n caselle in modo
tale che la somma dei numeri di ogni
riga, di ogni colonna e di ogni
diagonale sia sempre la stessa


Il numero di righe (e di colonne) si
chiama ordine del quadrato, mentre
la somma di una riga (o colonna o
diagonale) si chiama costante
magica.
Quante disposizioni di numeri in un
quadrato magico di ordine 4?


La tabella numerica di Subirachs ha una
costante magica uguale a 33, l'età di
Gesù Cristo quando fu crocifisso.
Questa tabella non è propriamente un
quadrato magico come quello du Durer
perché non contiene tutti i numeri da 1 a
16. Mancano il 12 e il 16 mentre il 10 e il
14 sono ripetuti due volte.
Il quadrato di Durer ha generato
quello di Subirachs . Come?
16
3
2
13
1
14
15
3
5
10
11
8
11
7
6
9
9
6
7
12
8
10
10
5
4
15
14
1
13
2
3
15
Composizioni di trasformazioni
geometriche nell’arte e nella natura
per condurre a scoprire isomorfismi
e a pensare per strutture come è
alla base della matematica moderna
link

Buona serata