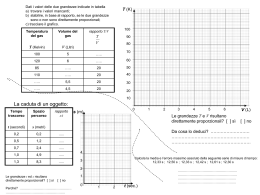
Il Metodo Scientifico
1.
2.
3.
4.
Il fenomeno d’interesse, sua idealizzazione
Le grandezze fisiche per descriverlo (unità)
Osservazione e misura (incertezze)
Formulazione di ipotesi: dal modello alla
legge fisica
5. Utilizzo della legge fisica per descrivere e
prevedere, caso falsificare l’ipotesi
Il Metodo Scientifico
h (m)
v (m/s)
t (s)
t=(1.20±0.01)× 102 s
v=(3.6±0.5)× 101 m/s
F =mg-qv !
F =mg ?
v =k t ?
v (m/s)
v =vlim(1-e-bt) !
t (s)
Il PUNTO materiale
multipli sottomultipli
Sistema Internazionale
Unità del Sistema Internazionale
Le buone maniere
GRANDEZZE DERIVATE nel S.I.
GRANDEZZE DERIVATE nel S.I.
GRANDEZZE DERIVATE nel S.I.
GRANDEZZE DERIVATE nel S.I.
Unità di misura e dimensioni
delle grandezze derivate
area = lunghezza x lunghezza
m2 = m x m
[L2]=[L]x[L]
Misure fisiche e incertezze
precisione e accuratezza di una misura
Misure fisiche e incertezze
• Numeri da matematici: 2, 3.0, √7, π, 4! …
• Numeri da fisici: 23.4 km, 23.41 km, 23,410 km, (80±1) s, …
• 3.0 = … 0003.000 … = 3
• 23.4 km ha TRE CIFRE SIGNIFICATIVE
• 23.41 km ha QUATTRO CIFRE SIGNIFICATIVE
• 0.027 s ha DUE CIFRE SIGNIFICATIVE
… 000 23.4 xxxx …
significative
incerta
non conosciute
Misure fisiche e incertezze
• d = 23.4 km
• d = [23.0 ÷ 24.0] km
• d = (23.5 ± 0.5) km
ATTENZIONE alla NOTAZIONE ESPONENZIALE
e alle CIFRE SIGNIFICATIVE
(23.5 ± 0.5) km
non diventano
• d = 23.41 km
• d = [23.40 ÷ 23.50] km
• d = (23.45 ± 0.05) km
(23500 ± 500) m
ma
(23.5 ± 0.5) x 103 m = (2.35 ± 0.05)x104 m
GUAI a USARE PIU’ CIFRE SIGNIFICATIVE di QUELLE … SIGNIFICATIVE!
(es: d=2.0; dπ=6.3 e non dπ=6.2831)
Incertezze nelle misure di lunghezza
strumento
incertezza
grandezza
inc. relativa