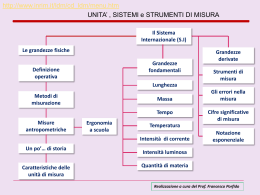
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Il Sistema
Internazionale (S.I)
Le grandezze fisiche
Grandezze
fondamentali
Definizione
operativa
Grandezze
derivate
Strumenti di
misura
Lunghezza
Metodi di
misurazione
Massa
Tempo
Misure
antropometriche
Ergonomia
a scuola
Caratteristiche delle
unità di misura
Cifre significative
di misura
Temperatura
Intensità di corrente
Un po’… di storia
Gli errori nella
misura
Notazione
esponenziale
Intensità luminosa
Quantità di materia
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
COSA SIGNIFICA
MISURARE
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Cosa significa misurare
GRANDEZZA FISICA
è tutto ciò che può essere misurato facendo ricorso
ad opportuni strumenti (distanza, peso, tempo, velocità,
temperatura, ecc.)
GRANDEZZE OMOGENEE
MISURARE
UNITÀ DI MISURA
MISURA
sono grandezze dello stesso tipo:
tutte le grandezze
fisiche con dimensione di lunghezza sono omogenee tra loro. Non
ha nessun senso confrontare una lunghezza con una massa, un
intervallo di tempo con una temperatura e nemmeno ha senso
sommarle tra loro.
Solo
le
grandezze
omogenee
tra
loro
possono
essere confrontate, sommate o sottratte.
significa confrontare la grandezza di cui voglio
conoscere la misura con un’altra che prendo come
campione, quindi significa dire quante volte l’unità
di misura è contenuta nella grandezza
è la grandezza, omogenea a quella da misurare,
scelta come campione
è il numero reale che si ottiene dal rapporto tra la
grandezza data e l’unità di misura
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Il risultato di una misurazione è sempre caratterizzato da tre parametri:
 Un valore numerico
 Una unità di misura
 Un’incertezza di misura
Per esempio, la misura della velocità che si legge sul tachimetro si scrive:
simbolo
Unità di misura
valore numerico
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
DEFINIZIONE
OPERATIVA
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Definizione operativa
Esempi di grandezze fisiche sono la lunghezza, il tempo, la velocità, la temperatura,
l’energia.
Il significato fisico di ciascuna di queste parole è fissato da una definizione operativa.
La definizione operativa di una grandezza fisica consiste di due parti:
• la descrizione degli strumenti necessari per misurare la grandezza
• la determinazione di una procedura non ambigua (detta “protocollo”) con cui utilizzare
gli strumenti di misura
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Per esempio, vediamo la definizione operativa della grandezza fisica «velocità».
L’idea intuitiva è che un oggetto più veloce percorre una distanza maggiore nello stesso tempo, oppure la
stessa distanza in un tempo minore.
Per descrivere questa intuizione con un numero, si introduce la velocità di un corpo attraverso la formula
Per misurare (e quindi definire) la grandezza fisica «velocità» (per esempio quella di un’automobile) abbiamo
bisogno di due strumenti di misura: un metro e un cronometro. Bisogna poi stabilire un protocollo:
 con il metro si misura la distanza
percorsa, individuata da due paletti
 Il cronometro parte quando il muso
dell’automobile è in corrispondenza
del primo paletto
 Il cronometro si arresta quando il
muso dell’automobile è all’altezza
del secondo paletto
Il valore indicato dal cronometro è il tempo impiegato. Avendo misurato una distanza di 90 m e un
tempo di 12 s, il valore della velocità è:
Un secondo sperimentatore che esegue la misura della
velocità della stessa auto, usando strumenti identici e lo
stesso protocollo, otterrà lo stesso risultato numerico (a
parte gli errori di misura che studieremo in seguito)
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
METODI DI
MISURAZIONE
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Metodi di misurazione
Per trovare la misura di una grandezza si possono seguire metodi diversi:
1) MISURA DIRETTA
2) MISURA INDIRETTA
3) MISURA CON STRUMENTI TARATI
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
UN PO’…
DI STORIA
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Un po’ … di storia
Inizialmente per quanto riguarda le unità di misura, quelle di lunghezza facevano per lo
più riferimento a parti del corpo umano: oltre al cubito (avambraccio), troviamo il
piede, il pollice, il passo.
Le superficie erano misurate in termini di terreno arabile da una coppia di buoi in un
giorno (iugero ≈ 2500 m²).
Sin dall' antichità per le principali unità di lunghezza e di peso si realizzarono campioni
che erano custoditi con cura religiosa, per lo più in templi o in luoghi sacri ed erano
imposti ai popoli conquistati.
Presso i Romani le unità di lunghezza erano il dito (1/16 del piede = 1,8525 cm), il
palmo (4 dita), il piede (quattro palmi = 29,64 cm), il passo (5 piedi = 74,1 cm), lo stadio
(125 passi = 185,25 m), il miglio (5000 piedi = 1,482 km) e la lega (7500 piedi = 2,223
km).
Nessuna regola particolare legava tra loro multipli e sottomultipli all'unità
fondamentale: il piede, il cui campione era custodito nel tempio di Giunone Moneta in
Campidoglio.
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Un po’ … di storia
La misura base per i liquidi era il moggio: pari a 8 ⅔
litro; l’anfora era ≈ 26 litri.
La misura base per i pesi era la libbra romana (≈ 327 g):
pari a ¾ della mina greca (≈ 436 g)
Anfora (Anphora)
Moggio (modius)
di bronzo
La groma
E' uno strumento di rilevazione per la misurazione della terra usato
nell'antica Roma sia per la definizione dei confini, che per le misurazioni
dei terreni o per l'assegnazione delle terre che venivano assegnate ai
soldati al congedo del loro servizio quale premio per il loro contributo
militare.
E' composta da un bastone di sostegno chiamato "ferramentum" che
veniva piantato al suolo e da quattro punte (cornicula) disposte a
perfetto angolo retto e che formano la croce terminale (groma) da cui
pendevano i quattro fili (nerviae) tesi da altrettanti contrappesi
(pondera). Lo strumento che raccordava il ferramentum con la
groma era il rostro che misurava esattamente un piede ("pes" 29,64 cm)
che costituiva l'unità base di lunghezza romana.
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Un po’ … di storia
Procedura per la costruzione delle città
Venivano tracciate le linee delle due strade principali
perpendicolari tra di loro all’intersezione di queste due linea c’era il
groma: in questo punto si realizzava il foro (la piazza principale
della città), mentre le estremità delle linee avrebbero coinciso con
le quattro porte della città.
Venivano tracciate delle linee parallele rispetto a questi assi
principali alla distanza di 100 actus ( uguale a 120 piedi = 3,56 km).
Il territorio veniva così suddiviso in 4 parti quadrate dette saltus .
Veniva tracciate altre strade parallele alla distanza tra loro di 20
actus (710,4 m). Le superfici quadrate così ottenute si chiamavano
“centurie” (≈ 50 ettari).
Ogni centuria era suddivisa in 10 strisce alla distanza tra loro di 2
actus (71,04 m).
La larghezze delle strade romane:
Decumano massimo: 40 piedi (11.84 mt)
Cardine massimo: 20 piedi (5.92 mt)
Limites quintarii: 12 piedi (3.55 mt)
Altre strade: 8 piedi (2.37 mt)
Realizzazione a cura del Prof. Francesco Porfido
UNITA’ , SISTEMI e STRUMENTI DI MISURA
MENU
NORD
100 actus
100 actus
DECUMANO MASSIMO 40 pes
EST
Porta
Pretoria
100 actus
OVEST
10 divisioni uguali
100 actus
saltus
centuria
20 actus
i lati della centuria
venivano divisi da linee
distanti tra loro 2 actus
(71,04 m)
CARDO MASSIMO 20 pes
20 actus
altre starde 8 pes
10 divisioni uguali
limites quintarii 12 pes
SUD
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Un po’ … di storia
Con la caduta dell'impero romano d'occidente e con il successivo
formarsi della società feudale la confusione dei sistemi di pesi e
misure fu enorme, essendo questi locali e propri di ciascun feudo.
Nel 789 Carlo Magno cercò di ovviare a questo disordine promulgando
un decreto sull'unificazione dei campioni di misura in tutto l'impero,
ma alla caduta dell'impero carolingio, con la moltiplicazione dei centri
di potere, si moltiplicarono le misure ufficiali, che si sovrapposero alle
misure locali o private che erano sopravvissute.
Lo sviluppo degli scambi marittimi e terrestri e l’interesse del fisco incrementò l'esigenza di
unificare in qualche modo i pesi e le misure e lungo i secoli furono fatti alcuni tentativi. Il
problema era avvertito anche dagli scienziati, che volevano far conoscere e confrontare i risultati
dei loro esperimenti.
Nel corso del 1700 si giunse a definire un insieme di campioni, almeno in alcuni paesi europei
come la Francia.
Infatti in Francia il 7 aprile 1795 si arrivò a pubblicare la tabella ufficiale dei multipli e
sottomultipli per quanto concerne le unità di lunghezza e massa e si costruirono i campioni (un
cilindro di platino per il kilogrammo ed un'asta pure di platino per il metro). Il presidente della
commissione che sviluppò il sistema metrico decimale, fu Joseph Louis Lagrange.
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Un po’ … di storia
• L’accademia delle Scienze
di Francia lavorò tra il 1790
e il 1799 alla scelta e alla
definizione di alcune unità
di misura: creò il S.M.D. (il
sistema metrico decimale).
• Perciò alla fine dell’800 i
sistemi più diffusi furono
due: il sistema metrico
decimale e quello
anglosassone.
• lunghezza
metro
• peso
kilogrammo
• tempo
secondo
Prevedeva anche la SUPERFICIE, il VOLUME e la
CAPACITA’
• lunghezza
• peso
• tempo
yarda
libbra
secondo
Realizzazione a cura del Prof. Francesco Porfido
MENU
entra
UNITA’ , SISTEMI e STRUMENTI DI MISURA
PROPRIETA’
FONDAMENTALI
DELLE UNITA’ DI
MISURA
Realizzazione a cura del Prof. Francesco Porfido
MENU
La Metrologia
UNITA’ , SISTEMI e STRUMENTI DI MISURA
è la scienza che studia i metodi da usare per la scelta
delle unità di misura e dei sistemi di misurazione
PROPRIETÀ
FONDAMENTALI DELLE
UNITÀ DI MISURA
1)UNIVERSALITA’
2)PERENNITA’
Hanno lo stesso valore in ogni luogo
Mantengono il loro valore fino a quando non vengono modificati
3)INDIPENDENZA
Sono fissati da accordi internazionali e i singoli Stati
non possono apportare modifiche
4)ACCESSIBILITA’
Chiunque è in grado da solo di effettuare la
misurazione di un oggetto
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
I sistemi di misura
L’insieme di varie unità di misura costituisce un
sistema di misura.
Costruire un SISTEMA DI UNITA DI MISURA ` significa essenzialmente:
• scegliere una determinata ripartizione delle grandezze fisiche tra fondamentali e derivate
• definire le unità di misura e gli eventuali campioni delle grandezze fondamentali
Un sistema di unità di misura è detto:
• completo se tutte le grandezze fisiche si possono ricavare dalle grandezze fondamentali
tramite relazioni analitiche
• coerente se le relazioni analitiche che definiscono le unità delle grandezze derivate non
contengono fattori di proporzionalità diversi da 1
• decimale se multipli e sottomultipli delle unità di misura sono tutti potenze di 10
I principali sistemi di misura adottati in passato sono:
Sistema di
lunghezza
peso
misura
cgs (1874)
MKS (1795)
.
Pratico o degli
ingegneri
tempo
Centimetri (cm)
Grammi (g)
Secondi (s)
Metro (m)
Chilogrammo-massa (kg)
Secondi (s)
Metro (m)
Chilogrammo-peso (kgp)
Secondi (s)
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
IL SISTEMA
INTERNAZIONALE
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Il sistema internazionale
I vecchi sistemi di misura sono ora
superati dal nuovo Sistema Internazionale
approvato nella Conferenza Generale dei
Pesi e delle Misure tenutasi a Parigi nel
1960.
Dal 1978 i Paesi dell’Unione Europea
sono tenuti ad adottare lo stesso sistema
di misura.
Chiamato semplicemente S.I.
Il sistema S.I. riconosce:
•7 grandezze fondamentali
•2 grandezza supplementari o secondarie
Il Sistema Internazionale è un sistema
decimale, e ha numerosi multipli e
sottomultipli in base 10.
Tutte le altre grandezze sono considerate
grandezze derivate, perché si ricavano da
quelle fondamentali mediante operazioni
di moltiplicazione o divisione.
Grandezza fondamentale Unità di misura Simbolo
Lunghezza
Metro
m
Massa
Chilogrammo
kg
Tempo
Secondo
s
Temperatura(1)
Grado Kelvin
K
Intensità corrente
elettrica
Ampere
A
Intensità luminosa
Candela
cd
Quantità di materia
Mole
mol
(1) In pratica la temperatura si misura in grado Celsius [ °C]
Grandezza
supplementare
Unità di misura Simbolo
Angolo piano (2)
Radiante
rad
Angolo solido
Steradiante
sr
(2) In pratica gli angoli si misurano in gradi sessagesimali [ °]
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Multipli e sottomultipIi del Sistema Internazionale
PREFISSO
SIMBOLO
VALORE NUMERICO
esa
E
1018
1 000 000 000 000 000 000
trilioni
peta
P
1015
1 000 000 000 000 000
biliardi
tera
T
1012
1 000 000 000 000
bilioni
giga
G
109
1 000 000 000
miliardi
mega
M
106
1 000 000
milioni
chilo
k
103
1 000
migliaia
etto
h
102
1 00
centinaia
deca
da
101
10
decine
100
1
unità
deci
d
10 -1
0,1
decimi
centi
c
10 -2
0,01
centesimi
milli
m
10 -3
0,001
millesimi
micro
μ
10 -6
0,000 001
milionesimi
nano
n
10 -9
0,000 000 001
miliardesimi
pico
p
10 -12
0,000 000 000 001
bimilionesimi
femto
f
10 -15
0,000 000 000 000 001
bimiliardesimi
atto
a
10 -18
0,000 000 000 000 000 001
trilionesimi
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
L’ortografia delle unità di misura
Le regole
Scrittura
corretta
Scrittura
scorretta
Il simbolo delle unità di misure segue il valore numerico
13,7 kg
kg 13,7
Il simbolo non va seguito dal puntino non essendo
un’abbreviazione
8m
8m.
60 W
60 Ws
60 Watts
L’unità di misura, quando non è accompagnata dal valore
numerico, si scrive per esteso
Alcuni metri
Pochi litri
Alcuni m
Pochi l
Se l’unità di misura si trova alla fine della frase si scrive per esteso
… è 10 metri.
… è 10 m.
I simboli di ora, minuto e secondo sono rispettivamente: h, min, s
8 h 9 min 3 s
8 hr 9’ 3”
I simboli monetari precedono sempre il numero a cui si riferiscono
$ 70
€ 28
70 $
28 €
Non si fa il plurale
Gli elementi che costituiscono una data in forma esclusivamente
numerica devono essere scritti nell’ordine seguente:
anno
mese
giorno
4 cifre
2 cifre
2 cifre
2012-01-01
01/01/2012
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
MISURE
ANTROPOMETRICHE
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
L'antropometria (dal greco antropos, uomo, e metron, misura)
Misure antropometriche è la scienza che si occupa di misurare il corpo umano
Il poter esprimere in parametri misurabili le caratteristiche
morfometriche individuali consente :
In età pediatrica: monitorare lo stato nutrizionale, i processi
fisiologici della crescita e le sue alterazioni (antropometria
auxologica)
In medicina sportiva: individuare le attitudini fisiche verso
specifiche attività sportive e personalizzare, ai fini del
raggiungimento delle migliori prestazioni agonistiche, le
tecniche e le metodiche di allenamento (antropometria
sportiva o chinantropometria)
In medicina legale: identificazione personale (antropometria
legale)
Nell’industria: indicazione di canoni ergonomici per la
progettazione del posto di lavoro, del posto di guida, etc.
Nell’industria dell’abbigliamento: determinazione delle taglie
corporee (antropometria ergonomica)
Uomo vitruviano di Leonardo da Vinci
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
La statura e il peso
LA STATURA e IL PESO vengono indicati come CARATTERI
FONDAMENTALI: caratteri che NON dovrebbero MAI
omettersi in rilevazioni antropometriche a qualsiasi scopo
effettuate.
STATURA:
ESPRESSIONE
SINTETICA
DELLE
MISURE
LONGITUDINALI; ad essa possono essere poi riportate le varie
dimensioni somatiche in modo da stabilire LE PROPORZIONI
CORPOREE.
PESO:
ESPRESSIONE
SINTETICA
DELLO
SVILUPPO
VOLUMETRICO ed in particolare dei SISTEMI SCHELETRICO E
MUSCOLARE.
Uomo vitruviano di Leonardo da Vinci
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
La statura e il peso
PESO OTTIMALE O DESIDERABILE:
formula usata dalle compagnie di
assicurazione
Peso [kg] = 50 + 0,75 x [statura (cm) – 150]
ESEMPIO: persona alta 169 cm
50 + 0,75 x [169-150] =
50 + (0,75 x 19) =
50 + 14,25 = 64,25 Kg
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
La statura e il peso
Il peso considerato a sé è di lieve importanza!!!!!
Da ciò l’opportunità di porlo in relazione ad altri caratteri, quali la statura stessa,
l’altezza del busto, il perimetro toracico, etc.
Modificando la formula del LIVI in Italia viene proposto L’INDICE BARICO (GiuffridaRuggeri)
dove St = Statura standard
La ricerca antropometrica ha cercato di individuare una RELAZIONE TRA PESO E ALTEZZA CHE SI
CORRELASSE MEGLIO ALLA COMPOSIZIONE CORPOREA e in particolare alla massa grassa (FM).
Tra i vari indici quello che ha incontrato il maggior consenso è L’INDICE DI QUETELET (1869) o BMI
(Body Mass Index)
VALORI BMI
FINO A 18,5
Da 18,5 - 24,9
Da 25 - 29,9
Da 30 - 34,9
Da 35 - 39,9
oltre 40
SOGGETTO
SOTTOPESO
NORMALE
SOVRAPPESO
OBESITÀ LIEVE
OBESITÀ MODERATA
OBESITÀ GRAVE
Limitazioni uso del BMI: scarsa sensibilità
nella misura dell’adiposità corporea nei
soggetti particolarmente piccoli o alti di
statura e incapacità di distinguere la
massa grassa dalla massa magra
indicando come obeso chi ha una massa
muscolare molto sviluppata.
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
La statura e il peso
In medicina dello sport si
parlerà di:
Normotipo se C = D
Brachitipo se C < D
Longitipo
se C > D
dove
C è la lunghezza delle gambe
D è la lunghezza del tronco
uomini
normotipi 51,1÷ 51,3
donne
52,5÷ 54,5
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
Taglia di un vestito
L'industria della confezione si avvale dei risultati derivati dalle analisi antropometriche che
consente la perfetta individuazione delle proporzioni di ogni soggetto, attraverso la rilevazione di
poche misure del suo corpo.
I dati raccolti confermano, senza ombra di dubbio, che la quasi totalità delle persone può essere
misurata e vestita industrialmente con ottimi risultati, rilevando tre parametri fondamentali di
misurazione: taglia, drop e statura.
TAGLIA: semicirconferenza del torace presa sopra la camicia
DROP o CONFORMAZIONE: differenza tra semicirconferenza del torace e semicirconferenza della vita
STATURA: altezza totale della persona rilevata con le scarpe
Ogni taglia può essere riferita alle seguenti conformazioni o drop che
possono cambiare a seconda della linea di stile:
• DROP 10 - conformazione extra snella – soggetto magrissimo
• DROP 7-8 - conformazione snella – soggetto magro
• DROP 6 - conformazione normale – soggetto normale
• DROP 4 - conformazione mezza forte – soggetto robusto
• DROP 2 - conformazione forte – soggetto prominete
• DROP 0 - conformazione extra forte – soggetto panciuto
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
Misura della scarpa
La misura della scarpa è una indicazione numerica delle sue dimensioni.
Per la misura delle scarpe ci sono diversi sistemi di misurazione.
I diversi sistemi differiscono sia per la nazione sia per il diverso tipo di scarpa (ad
esempio, degli uomini, delle donne, dei bambini, lo sport o le scarpe di sicurezza).
La misura della scarpa viene determinata da un numero; questo numero può essere
impresso:
 sulla suola delle scarpe: si ha un numero sulla suola delle scarpe
 sulla soletta si ha il numero dentro la scarpa, o più in generale nella zona di
contatto con il piede
 sull‘etichetta che generalmente è posta sulla tomaia
Per calcolare la dimensione in base alla lunghezza effettiva piedi,
si deve prima aggiungere una lunghezza di circa 1,5 a 2 cm :
Relazione tra altezza e lunghezza piede
• uomo lunghezza piede = 15% altezza
• donna lunghezza piede = 14,5% altezza
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Misure antropometriche
Misura della scarpa
Scale di conversione
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
LA MISURA DELLA
LUNGHEZZA
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura della lunghezza
UNITÀ DI MISURA
La lunghezza è una grandezza fondamentale del
S.I.
MULTIPLI E SOTTOMULTIPLI
Metro [ m ]
 Nel marzo 1791 il metro fu definito come la decimilionesima parte dell’arco meridiano terrestre dal
Polo Nord all’Equatore passante per Parigi (poco pratica non riproducibile).
Nel 1875 si abbandona l’idea di ancorare la lunghezza del metro alle
dimensioni della Terra e si costruisce un nuovo metro campione, costituito
di una sbarra a X in lega di platino (90%) e iridio (10%) depositato a
Sèvres presso Parigi , nei sotterranei dell’Ufficio Internazionale Pesi e Misure.
In Italia una copia del metro campione è conservata presso l’Istituto di Metrologia “Gustavo
Colonnetti” del CNR a Torino
 Dal 1983 il metro è definito come la distanza che la luce percorre nel vuoto in un intervallo di tempo
di 1/299 792 458 di secondo.
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Nome
Simbolo
Valore numerico
chilometro
km
1000
ettometro
hm
100
decametro
dam
10
metro
m
1
decimetro
dm
0,1
centimetro
cm
0,01
millimetro
mm
0,001
SI DIVIDE PER 10
SI MOLTIPLICA PER 10
Multipli e sottomultipli del
metro
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura della lunghezza
APPROFONDIMENTO
• Un sottomultiplo del metro, usato per grandezze visibili al microscopio, è il millesimo di
millimetro cioè il micrometro [μm]
1 μm = 10-3 mm = 10-3 ∙ 10-3 m = 10-6 m
• Il nanometro, il cui simbolo è nm, è 1millesimo di micron e quindi 1 miliardesimo di metro
1 nm = 10-3 μm = 10-3 ∙ 10-6 m = 10-9 m
• L’Angström, il cui simbolo è Å, è 1 decimo di nanometro e quindi 1 decimiliardesimo di
metro
1 Å = 10-1 nm = 10-1 ∙ 10-9 m = 10-10 m
Per distanze astronomiche si intendono quelle distanze tipiche tra
i sistemi stellari del nostro universo
•
L’unità astronomica (ua) è la distanza media Terra – Sole
1 ua = 149 600 000 km = 1,496 ∙ 108 km
•
•
Anno luce (a.l.) è la distanza percorsa in un anno dalla luce nel vuoto, che viaggia a circa
300 000 km/s
1 a.l. = 9 463 miliardi di km = 9,463 ∙ 1012 km
•
Parsec (pc) distanza dalla Terra di una stella che ha un parallasse di 1 secondo d’arco
1 pc = 30 900 miliardi di km = 3,09 ∙ 1013 km
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura della lunghezza
La storia del metro
Le unità astronomiche
Realizzazione a cura del Prof. Francesco Porfido
L’area è una grandezza derivata del S.I.
La misura dell’area
UNITÀ DI MISURA
MULTIPLI E SOTTOMULTIPLI
Metro quadrato [ m² ]
Il metro quadrato è l’area di un quadrato che ha il lato lungo 1 metro.
1m
1 m²
1m
La misura del volume
Il volume è una grandezza derivata del S.I.
UNITÀ DI MISURA
MULTIPLI E SOTTOMULTIPLI
Metro cubo [ m³ ]
Il metro cubo è il volume di un cubo che ha lo spigolo lungo 1 metro.
1m
1 m³
1m
1m
La misura della capacità
La capacità è il volume del recipiente che
contiene completamente un liquido e
corrisponde alla quantità di liquido che è
contenuto nel recipiente
UNITÀ DI MISURA
MULTIPLI E SOTTOMULTIPLI
Litro [ l ]
 Il litro è la quantità di acqua distillata a 4 °C che riempie completamente un cubo cavo che
ha il volume di 1 decimetro cubo.
1 dm
1 dm³ = 1 l
1 dm
1 dm
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
LA MISURA DELLA
MASSA
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura della massa e …
del peso
UNITÀ DI MISURA
Chilogrammo [ kg ]
La massa è una grandezza fondamentale
del S.I.
MULTIPLI E SOTTOMULTIPLI

Il chilogrammo campione è costituito da un cilindretto, dimensioni ø 39 mm e
h = 39 mm,in lega di platino (90%) e iridio (10%) depositato a Sèvres presso
Parigi , nei sotterranei dell’Ufficio Internazionale Pesi e Misure.
Il chilogrammo è la massa di 1 dm³ di acqua distillata alla temperatura di 4 °C.

Il peso è una forza : è la forza con cui un corpo viene attratto verso il centro
della Terra.
L’unità di misura della forza è il Newton [N].
Più il corpo si avvicina al centro della Terra e più il suo peso aumenta.

Peso e massa non sono la stessa cosa.
Quanto pesa un oggetto sulla Luna?
La quantità di materia (la massa) che costituisce l’oggetto non cambia,
mentre ciò che cambia è il peso: sulla Luna l’oggetto è sei volte più
leggero rispetto alla Terra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
Nome
Simbolo
Valore numerico
Megagrammo
Mg (t)
1000 000
quintale
q
100 000
miriagrammo
mag
10 000
chilogrammo
kg
1 000
ettogrammo
hg
100
decagrammo
dag
10
grammo
g
1
decigrammo
dg
0,1
centigrammo
cg
0,01
milligrammo
mg
0,001
SI DIVIDE PER 10
SI MOLTIPLICA PER 10
Multipli e sottomultipli del
chilogrammo
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
APPROFONDIMENTO
•RELAZIONE TRA CAPACITA’, VOLUME e MASSA
Ricorda che per l’acqua distillata a 4 °C:
1 l = 1 dm³ = 1 kg
ESEMPIO:
25 m³ = …… q
25 m³ = 25 000 dm³ = 25 000 kg = 250 q
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura del peso
Il dinamometro
Isacco Newton
La forza di gravità
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
LA MISURA DEL TEMPO
entra
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura del tempo
Il tempo è una grandezza fondamentale
del S.I.
UNITÀ DI MISURA
Secondo [ s ]
MULTIPLI E SOTTOMULTIPLI
 L’uomo primitivo si accorse che certi fenomeni naturali, come il sorgere o il calare del sole, o il
moto della Luna intorno alla Terra, si verificavano con regolarità secondo determinati periodi di
tempo: da queste osservazioni derivano i primi calendari (5000 anni fa).
 Per misurare intervalli più brevi furono inventati,dai Babilonesi, gli orologi solari o meridiane,
che indicavano l’ora durante il giorno per mezzo della proiezione dell’ombra di un’asta (gnomone)
sopra una base opportunamente orientata e graduata.
 Gli Egiziani introdussero l’uso della clessidra, formata da due recipienti che sono in
comunicazione tra loro con un forellino, attraverso il quale scorre acqua o sabbia.
 La scoperta delle leggi che regolano il moto del pendolo, l’invenzione delle molle a bilanciere
e degli ingranaggi, portarono alla costruzione di orologi sempre più precisi e perfetti, sino a
giungere agli orologi a cristallo e a quelli atomici.
 L’unità di misura della durata del tempo è basata su un fenomeno astronomico: la durata del giorno
solare.
Il GIORNO SOLARE è il tempo che intercorre tra due passaggi successivi del sole allo stesso meridiano.
Il GIORNO SOLARE MEDIO è stato suddiviso in 24 intervalli uguali: le ORE
L’ora è suddivisa, a sua volta, in 60 intervalli uguali: i MINUTI
Il minuto è suddiviso in 60 intervalli uguali: i SECONDI
 Il secondo è la 86 400 esima parte del giorno solare medio
 Nel 1971 il secondo è definito riferendolo alla durata delle oscillazioni della radiazione emessa dall’atomo del
Cesio 133.
Realizzazione a cura del Prof. Francesco Porfido
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
La misura del tempo
La storia del calendario
Realizzazione a cura del Prof. Francesco Porfido
La misura della
temperatura
UNITÀ DI MISURA
Grado Kelvin [ K ]
La temperatura è una grandezza
fondamentale del S.I.
SCALE TERMOMETRICHE
La temperatura è la misura del livello termico di un corpo, cioè ci dice quanto un corpo è
caldo o freddo, però non ci dà l’indicazione della quantità di calore contenuta nel corpo.
Lo strumento che misura la temperatura è il termometro.
Il tipo più comune di termometro è costituito da un tubicino di vetro
collegato a un bulbo. All’interno del bulbo si trova un liquido colorato
o mercurio. Di fianco al tubo di vetro si trova una scala graduata.
Il funzionamento del termometro si basa sulla dilatazione dei corpi
quando sono riscaldati.
Il calore è una forma di energia, cioè è l’energia di movimento posseduta dalle particelle
che formano un corpo, perciò è la causa che fa elevare la temperatura di un corpo.
L’unità di misura del calore è la chilocaloria [kcal]. Nel sistema SI è lo joule [J]
Una chilocaloria è la quantità di calore che deve essere fornita a 1 kg d’acqua per
fare aumentare la sua temperatura da 14,5 a 15,5° C.
La scala Celsius
Celsius
Intervallo suddiviso in 100 parti
100 Temperatura dell’acqua bollente
0
Temperatura del ghiaccio
fondente
La scala Celsius o centigrada ha preso
come riferimenti il punto di
congelamento (valore 0) e il punto di
ebollizione (valore 100) dell’acqua a
livello del mare, cioè a temperatura e
pressione standard (TPS).
L'intervallo fra questi due riferimenti
è stato suddiviso in 100 parti uguali,
dette gradi centigradi.
Il simbolo del grado centigrado è °C.
APPROFONDIMENTO
La scala Celsius prende nome dall'astronomo,
fisico e matematico svedese Anders Celsius
(1701-1744).
La scala Fahrenheit
Fahrenheit
Intervallo suddiviso in 180 parti
212 Temperatura dell’acqua bollente
32
Temperatura del ghiaccio
fondente
La scala Fahrenheit, usata nei paesi
anglosassoni, utilizza gli stessi
riferimenti della scala Celsius ma
attribuisce a questi riferimenti i valori
32 e 212.
L’intervallo tra questi due valori è di
180 gradi.
Il grado Fahrenheit è, quindi, minore
di quello centigrado.
Il simbolo del grado Fahrenheit è °F.
APPROFONDIMENTO
La scala Fahrenheit è così chiamata in onore del fisico e
ingegnere tedesco Daniel Gabriel Fahrenheit (1686 – 1736),
che la propose nel 1724. È meglio conosciuto per aver
inventato il termometro ad alcool (1709) ed il termometro a
mercurio. Scoprì che il punto di congelamento e che il punto
di ebollizione dei liquidi varia a seconda della pressione
atmosferica.
La scala Kelvin
Kelvin
Intervallo suddiviso in 100 parti
373 Temperatura dell’acqua bollente
273
Temperatura del ghiaccio
fondente
In ambito scientifico è utilizzata la
scala Kelvin. Lo zero Kelvin
corrisponde a una temperatura
teoricamente irraggiungibile (zero
assoluto).
Lo 0 assoluto Kelvin corrisponde la
temperatura di -273,15 °C. Un grado
Kelvin corrisponde a un grado
centigrado.
Il simbolo 12 K si legge 12 Kelvin.
APPROFONDIMENTO
La scala Kelvin prende nome dal fisico e ingegnere irlandese
William Thomson (Belfast, 26/6/1824 – Netherhall,
17/12/1907), nominato barone con il nome di Lord Kelvin
(nome di un fiume che scorre presso Glasgow). Inventore del
telegrafo elettrico, che gli procurò una maggiore
considerazione da parte dell'opinione pubblica e gli assicurò
fama e ricchezza.
SCALE TERMOMETRICHE
373
273
Réaumur
80
212
32
Intervallo suddiviso in 80 parti
Intervallo suddiviso in 100 parti
Intervallo suddiviso in 100 parti
100
0
Fahrenheit
Kelvin
Intervallo suddiviso in 180 parti
Celsius
Temperatura dell’acqua bollente
0
Temperatura del ghiaccio
fondente
APPROFONDIMENTO
Tk = Tc + 273
Esempio:
Tc = Tk – 273
Tc = 30 °C
Tk = 343 K
Tk = 30 + 273 = 303 K
Tc = 343 – 273 = 70 °C
Tc/100 = (Tf -32)/180
Esempio: Tc = 30 °C
Tf = 68 °F
Tf = 32 + Tcx180/100 = 32 + 30x180/100 = 86 °F
Tc = (Tf -32)x100/180 = (68 -32)x100/180 = 20 °C
Gli strumenti di misura
CARATTERISTICHE
DEGLI STRUMENTI DI
MISURA
Uno strumento di misura è un dispositivo
destinato a fare una misurazione
Lo strumento può presentarsi come un singolo
oggetto, oppure può essere composto da due o
più elementi che, opportunamente combinati,
permettono di eseguire la misura
1)PORTATA
è la misura massima che lo strumento riesce a dare
2)SENSIBILITA’
è la capacità che ha lo strumento di accertare piccole variazioni di
valore (indica la misura più piccola che lo strumento riesce a rilevare)
3)PRECISIONE
indica il grado di accuratezza della misura effettuata, perciò indica
lo scostamento della misura rilevata rispetto a quella reale.
4)PRONTEZZA
è il tempo impiegato dallo strumento a dare la misura
5)FEDELTA’
è la capacità di fornire lo stesso valore in seguito a varie misurazioni
Uno strumento non ha tutte queste caratteristiche insieme.
La scelta dello strumento va fatta, perciò, in funzione di ciò che devi misurare.
Gli strumenti di misura
Gli strumenti di misura possono essere
analogici o digitali
STRUMENTO
ANALOGICO
STRUMENTO
DIGITALE
IL VALORE DELLA MISURA SI
LEGGE SU UNA APPOSITA
SCALA GRADUATA
IL VALORE DELLA MISURA
APPARE COME UNA
SEQUENZA DI CIFRE
La parola “digitale” deriva
dall’inglese “digit”, che
significa “cifra”.
Metro a
nastro
Orologio a
lancette
Voltometro
ad ago
Metro ad
ultrasuono
Orologio
al quarzo
Voltometro
elettronico
Nessuna misurazione è in grado di fornire un risultato esattamente
uguale al valore vero della grandezza misurata.
Ciò significa che qualsiasi misura è soggetta a errore,
chiamando errore di misura la differenza fra il valore effettivo della
grandezza e quello misurato.
Gli errori nelle
misure
PER SAPERE QUAL E’ LA MISURA PIU’ ATTENDIBILE … si fanno più misurazioni della stessa
grandezza e si calcola la media aritmetica
TIPI DI ERRORI
SISTEMATICI
ACCIDENTALI
dipende dallo strumento che può
dare sempre una misura in eccesso
o in difetto
dipende da cause non prevedibili dovute
sia al modo di effettuare la misurazione,
sia al soggetto che la compie
Errata scelta dello strumento
Caso
Errori dovuti all’usura
Imprecisione
dell’operatore
Errate graduazioni dello strumento
Deformazioni elastiche delle parti
dello strumento
Gli errori nelle
misure
La misura di una grandezza fisica fornisce un suo valore
approssimato, espresso nella forma:
x = M ± εa (detto intervallo di incertezza)
Se la misura è eseguita con uno strumento a bassa sensibilità, la
ripetizione della misura, nelle stesse condizioni, fornisce sempre lo
stesso valore M (il valore centrale fra le due tacche). In questo caso
εa è dato dalla semiampiezza dell’intervallo minimo misurabile
(sensibilità dello strumento).
Esempio:
M = 7,5 kg
ε a = (10-5)/2 = 2,5 kg
O
5
10 kg
x = M ± εa = 7,5 ± 2,5 kg
Se la misura è eseguita con uno strumento ad alta sensibilità, la ripetizione della misura, nelle stesse condizioni,
fornisce valori diversi. In questo caso M rappresenta la media aritmetica delle misure e εa rappresenta la stima
dell’errore.
Errore assoluto o errore massimo
La stima dell’errore può essere dato: εa = (Xmax - Xmin)/2
Esempio: x1 = 24,8 cm x2 = 25,1 cm
x3 = 25,5 cm
x4 = 25,8 cm
M = (x1 + x2 + x3 + x4)/4 = (24,8+ 25,1 + 25,5 + 25,8)/2 = 101,2/4 = 25,3 cm
εa = (Xmax - Xmin)/2 = (25,8 – 24,8)/2 = 1,0/2 = 0,5 cm
x = M ± εa = 25,3 ± 0,5 cm
24,7
24,8
25,0
Valore medio
25,3
Errore massimo
25,5
25,8
Gli errori nelle
misure
Osserviamo le seguenti tre misure:
x1 = 23,5 ± 0,5 m
x2 = 10,4 ± 0,5 m
x3 = 5,3 ± 0,5 m
Hanno tutte lo stesso errore assoluto εa =0,5 m . Dove siamo stati più precisi ?
Errore relativo ed errore percentuale
Appare chiaro che un errore di 0,5 m su una misura di 5,3 m è più grave di un errore di 0,5 m su una di 23,5 metri .
Per evidenziare questa differenza si introduce l’errore relativo.
L’errore relativo è il rapporto fra l’errore assoluto εa e il valore medio M della misura (n° adimensionale).
Esso indica il grado di precisione di una misura (più piccolo è tale valore, minore è l’errore).
In simboli:
ε r = εa / M
Nei tre esempi:
ε r = 0,5/23,5 = 0,02
ε r = 0,5/10,4 = 0,05
ε r = 0,5/5,3 = 0,09
L’errore percentuale è dato dal prodotto dell’errore relativo per 100. In simboli: η = 100 ε r % .
Modalità di scrittura di una misura
Per scrivere correttamente una misura affetta da errore occorre utilizzare le seguenti indicazioni:
La misura deve contenere lo stesso numero di cifre decimali dell’errore.
Esempi:
(5,852 ± 0,001) m è una scrittura corretta.
(5,8527 ± 0,001)m non è una scrittura corretta. (5,85 ± 0,001) m non è una scrittura corretta.
In generale, non essendo possibile conoscere l’errore con un elevato numero di cifre, è buona norma scriverlo con
al massimo due cifre decimali.
Esempio: anziché scrivere (5,852739 ± 0,000001)m, è più corretto scrivere (5,85 ± 0,01) m.
Cifre significative
di un misura
Le cifre significative di una misura sono le cifre note con
certezza più una incerta.
La misura della lunghezza di un campo da gioco è:
Cifre certe
Numero
13
21,3
21,30
4720
0,3
0,03
•
•
•
(136 ± 2) m
Cifra incerta
Cifre significative
2
3
4
4
1
1
Tutte le cifre sono significative nel caso in cui il valore della prima e dell’ultima cifra
del valore di una misura sono diverse da zero.
Se invece il numero inizia con lo zero e la virgola, sono significative solo le cifre a
partire dalla prima diversa da zero:
0,00631 kg
ha 3 cifre significative infatti 0,00631 kg può essere espresso come
6,31 g o come 6,31 x 10-3 kg.
Gli zeri sono considerati cifre significative dopo la virgola o in mezzo al numero.
Arrotondamenti
Arrotondare un numero significa sostituirlo con un altro che
abbia meno cifre significative in modo che se l’ultima cifra
risulta maggiore di 5 si aggiunga un’unità all’ultima cifra
significativa, se minore si sottragga. Se l’ultima cifra residua è 5
è necessario considerare la penultima cifra significativa: se
questa è pari l’ultima cifra rimane 5, se la penultima è dispari il
5 viene aumentato a 6
Esempio :
il numero 7,3476 , che ha 5 cifre significative, diventa
•7,348 arrotondato a 4 cifre significative
•7,35 arrotondato a 3 cifre significative
•7,3 arrotondato a 2 cifre significative
Quando si eseguono dei calcoli, per non alterare il grado di precisione, è necessario
ricordare tre importanti regole:
 Per la moltiplicazione e divisione di una misura per un numero il risultato deve
avere le stesse cifre significative della misura;
 per l’addizione e la sottrazione di misure il risultato deve contenere lo stesso
numero di decimali della misura che ne contiene il minor numero;
 per la moltiplicazione e la divisione di misure il numero delle cifre significative nel
risultato non deve essere maggiore di quello della misura meno precisa.
In generale vale la seguente regola:
Cifre significative
nelle operazioni
Il numero di cifre significative del risultato di
un'operazione tra misure è uguale al numero di cifre
significative della misura che ha precisione minore.
MOLTIPLICAZIONE E DIVISIONE DI UNA MISURA PER UN NUMERO
Il risultato deve avere le stesse cifre significative della misura
20 m : 5 = 4 m
No!
Perché la misura (20 m) ha 2 cifre significative perciò il risultato deve avere 2 cifre
significative quindi:
20 m : 5 = 4,0 m
5,87 s x 4 = 23,48 s
No!
Perché la misura (5,87 s) ha 3 cifre significative perciò il risultato deve avere 3 cifre
significative quindi:
5,87 s x 4 = 23,5 s
Cifre significative
Le cifre significative nelle operazioni
MOLTIPLICAZIONE E DIVISIONE DI MISURE
Il risultato deve avere lo stesso numero di cifre significative della misura meno precisa
5,870 m x 2,5 m = 14,675 m2
No!
Perché la misura meno precisa (2,5 m) ha 2 cifre significative perciò il risultato deve
avere 2 cifre significative quindi:
5,870 m x 2,5 m = 15 m2
48,2 km : 3,7524 h = 12,8455125 km/h
No!
Perché la misura (48,2 km) ha 3 cifre significative perciò il risultato deve avere 3 cifre
significative quindi:
48,2 km : 3,7524 h = 12,8 km/h
Cifre significative
Le cifre significative nelle operazioni
ADDIZIONE E SOTTRAZIONE DI MISURE
Il risultato deve avere lo stesso numero di cifre significative della misura meno precisa
31,9
m +
23
m +
4,7354 m =
Nel calcolo si sommano
numeri con precisione
diversa
Li
approssimiamo
in
modo da allinearli con il
numero che l’incertezza
più grande
31,9
32
23
4,7354 5
m +
m +
m =
In tal modo si scrive il
risultato con il numero
corretto
di
cifre
significative
32
23
5
60
m +
m +
m =
m
Notazione
scientifica
(esponenziale)
In Fisica si incontrano grandezze le cui misure sono espresse da
numeri molto grandi o molto piccoli.
E’ molto scomodo e laborioso scrivere questi numeri ed effettuare
calcoli con essi.
Questi numeri possono essere rappresentati come prodotto di un
numero ≥ 1 ma < di 10 per una potenza del 10.
Questo tipo di rappresentazione è detta notazione scientifica.
L’esponente può essere positivo o negativo
Esempio :
73.400.000.000.000.000.000.000
0,000 000 000 01
7,34 • 1022
1 • 10-11
Nel caso in cui si eseguono calcoli utilizzando numeri espressi con notazione esponenziale
è bene ricordare che:
addizione e sottrazione si possono eseguire solamente fra numeri con le stesse potenze
di 10:
7,4 • 103 + 3,27 • 103 = 10,67• 103 o meglio 11 • 103
per la moltiplicazione è necessario moltiplicare i coefficienti e sommare gli esponenti di
10:
6,02 • 1023 x 3,27 • 10 -2 = 19,68 • 1021 o meglio 1,97 • 1022
nella divisione è necessario dividere i coefficienti e sottrarre gli esponenti di 10:
MENU
UNITA’ , SISTEMI e STRUMENTI DI MISURA
ERGONOMIA
A SCUOLA
entra
Realizzazione a cura del Prof. Francesco Porfido