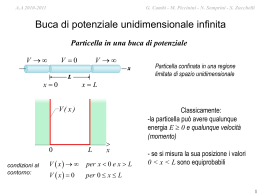
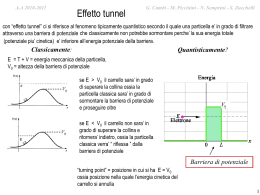
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
Particella libera in moto non relativistico
Classicamente:
• Velocità (momento) qualunque (compreso v = 0) e costante
• Posizione x(t), moto rettilineo
• Energia totale pari all’energia cinetica E = p2/2m, può assumere qualunque valore E 0, se E = 0 la particella è in quiete
Quantisticamente:
• Potenziale nullo V = 0, e nessuna condizione al contorno quindi la particella possiedera’ soltanto energia cinetica
l’equazione di Shroedinger indipendente dal tempo sara’
 2

 E
2
2m x
2
 ( x)  Aeikx  Beikx
in effetti se V = 0 l’equazione di Shrodinger indipendente dal tempo
diviene
d 2  x 
dx
2

2mE
2
  x
da cui
d 2  x 
dx
2
2mE
k

2
1
2m   x 
 k 2  x 
d 2  x 
dx
2
dove si e’ posto
E
dato che
E0
k  2mE /
d 2 ( x)
 k 2 ( x)  0
dunque, come gia’ evidenziato in precedenza, l’ equazione si riconduce a
2
dx
ossia all’ equazione dell’oscillatore armonico semplice per risolvere questa equazione si ricorre all’equazione
algebrica associata ossia si procede supponendo che la soluzione possa essere del tipo
 ( x)  e x
1
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
quindi si ha
d ( x)
  e x e
dx
2
2
   k

d 2 ( x)
x
2
2
2 x
2 x
2 x
dunque


e

e

k
e

0
e
(


k
)0

dx 2
2mE
ik in conclusione esistono due soluzioni immaginarie    i
e per il principio di sovrapposizione se
 ( x)  c1eikx  c2eikx
 ( x)  eikx
e
 ( x)  eikx
sono soluzioni allora anche
sara’ una possibile soluzione in generale c1 e c2 saranno numeri complessi
il significato delle due soluzioni si comprende appieno applicando l’operatore impulso alle funzioni
ikx
d’onda ottenute  ( x)  e
ovvero
pˆ x ( x)  k ( x)
e
 ( x)  eikx
pˆ x eikx  i
d ikx
e  i 2 keikx
dx
da cui
pˆ x eikx  keikx
quindi eikx e’ un autofunzione dell’operatore impulso con autovalore
qualsiasi valore di E positivo e’ accettabile e non si ha quantizzazione dell’energia
k  2mE
G. Cambi – S. Zucchelli – M. Piccinini
A.A. 2009-2010
analogamente
pˆ x e  ikx  i
d  ikx 2 ikx
e  i ke
da cui
dx
pˆ x e  ikx   ke  ikx ovvero
pˆ x ( x)   k ( x)
quindi anche e-ikx e’ una autofunzione dell’operatore impulso con autovalore negativo  k   2mE
ricapitolando:
nello stato rappresentato da eikx la particella si muove lungo l’asse x con quantita’ di moto
px  k
quindi si muove lungo la direzione positiva dell’asse x
nello stato rappresentato da e-ikx la particella si muove lungo l’asse x con quantita’’ di moto
px   k
quindi si muove lungo la direzione negativa dell’asse x
gli stati stazionari della particella libera,
ossia le soluzioni dell’equazione di Shroedinger
dipendente dal tempo corrispondono alle funzioni
eikx et  ei ( kx t )
e
ikx
e e
E
 t
e
e
 ikx
e
E
 t
e  ikx e t  e  i ( kx t )
si tratta di onde piane di probabilita’ progressive e regressive lungo l’asse x
e dato che
E

G. Cambi – S. Zucchelli – M. Piccinini
A.A. 2009-2010
saremmo percio’ portati a concludere che un onda piana di probabilita’ rappresenta una particella libera
ma cio’ sarebbe un errore perche’ una funzione d’onda del tipo
non e’ normalizzabile in quanto
 ( x, t )  ei ( kx t )






( x, t )   * ( x, t )( x, t )dx   ei ( kxt )ei ( kxt ) dx   1 dx  
2
e un discorso analogo vale per una funzione del tipo
( x, t )  ei ( kx t )
quindi un’onda piana di probabilita’ non puo’ rappresentare una particella libera
cosa peraltro gia’ nota dato che sappiamo che una particella quantistica e’ rappresentata da un pacchetto d’onde
ma anche nei fenomeni ondulatori classici le onde piane erano da considerarsi come astrazioni
utili tuttavia , grazie al teorema di Fourier per costruire funzioni matematiche con un preciso senso fisici
in perfetta analogia nel caso quantistico utilizzeremo le soluzioni in onde piane per
costruire soluzioni che siano combinazioni lineari di onde piane e che descrivano stati fisici
G. Cambi – S. Zucchelli – M. Piccinini
A.A. 2009-2010
in conclusione:
la soluzione generale dell’equazione di Shroedinger dipendente dal tempo che descrive gli stati stazionari di
particella libera è :
 E ( x, t )   c1e  c2 e
ikx
 ikx
e
E
i t
 c1e
i kx t 
 c2e
 i kx t 
dove  
E
la soluzione e’ data dalla sovrapposizione di due esponenziali oscillanti in generale dovremo quindi prepararci
ad avere soluzioni costituite da somme di onde progressive e regressive
tutte le energie sono ammesse (nessuna quantizzazione), ma gli stati stazionari non sono stati fisici
in effetti non esiste in natura una particella libera con energia definita perche’ la particella libera fisica è un
pacchetto d’onde …
 ( x, t ) 
1
2



c(k )ei kxt dk
con frequenze vicine tra loro di modo che
dove
E part
c(k ) 
1
2



 ( x,0)e ikx dx
m v part  vg 
k
d
 m
dk
m
G. Cambi
M. Piccinini
- N. Semprini
- S. Zucchelli
G.- Cambi
– S. Zucchelli
– M. Piccinini
A.A
A.A.2010-2011
2009-2010
in presenza di un potenziale V0 costante per garantirsi che le soluzioni siano normalizzabili in genere basta imporre
che l’energia cinetica sia sempre positiva di modo che sia sempre E > V0 anche nel caso l’energia totale E fosse
negativa
nota bene:
nel caso particolare della particella libera, V0 = 0 , porre E > 0 non ha comunque portato a soluzioni normalizzabili e
anche se E fosse stata negativa le soluzioni sarebbero state costituite da esponenziali reali
ed essendo tali funzioni non normalizzazabili
quando integrate su tutto l’asse reale ossia per  ∞ < x <  ∞
sarebbero da scartare
ma attenzione
se gli esponenziali reali fossero da integrare in intervalli dell’asse reale
per esempio solamente tra  ∞ < x < 0
oppure solamente tra 0 < x < + ∞
scelta la combinazione opportuna di esponenziali reali , potrebbero essere nomalizzabili
dobbiamo quindi prepararci ad accettare l’eventualita, proibita classicamente, che l’energia cinetica possa assumere
anche valori negativi, come potrerbbe succedere nel caso particolare in cui si abbia E < 0 con V = 0
6